На чем основано математическое моделирование

Математическое моделирование основано на применении математических методов и алгоритмов для создания абстрактных моделей реальных систем. Оно позволяет предсказывать поведение системы, проводить эксперименты и оптимизировать процессы, что является важным инструментом в научных и инженерных исследованиях, экономике и других областях знания.

Математическое моделирование является важной и широко применяемой областью науки. Оно позволяет описать и понять различные физические, химические, экономические и социальные процессы с помощью математических моделей. Математическое моделирование основывается на применении математических методов и алгоритмов для создания упрощенных, но реалистичных представлений о реальности.

Основные принципы математического моделирования включают абстракцию, упрощение, формализацию и верификацию моделей. Абстракция заключается в выборе существенных характеристик процесса и игнорировании несущественных деталей. Упрощение позволяет сделать модель более простой и понятной, но при этом сохранить ее достаточную точность для решения задачи. Формализация заключается в переводе реального явления в математические выражения и уравнения. Верификация представляет собой проверку модели на соответствие реальным данным и экспериментам.

Математическое моделирование находит применение во многих областях, начиная от физики и инженерии, где оно используется для моделирования физических систем и разработки новых технологий, и заканчивая экономикой и социологией, где моделирование позволяет анализировать поведение рынка, прогнозировать экономические показатели и изучать социальные процессы. Также математическое моделирование играет важную роль в медицине, биологии, экологии, психологии и других научных и прикладных областях, где оно помогает понять и предсказать сложные процессы и явления.

Математическое моделирование является неотъемлемой частью современной науки и практического применения. Оно позволяет углубить наше понимание мира, предсказывать будущие события и разрабатывать новые решения и технологии. Использование математических моделей позволяет сэкономить время, ресурсы и снизить риски при решении различных задач. Владение основами математического моделирования является необходимым навыком для многих специалистов и открывает широкие возможности для исследования и применения математических методов в различных областях знания.

Определение и основные принципы

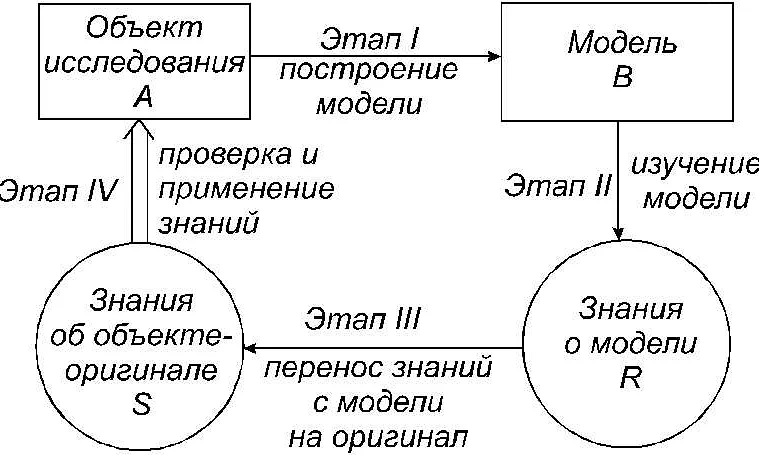
Основные принципы математического моделирования включают:

1. Выбор системы исследования: определение реальной системы или явления, которую необходимо изучить.
2. Формулировка целей и задач: определение целей моделирования и постановка конкретных задач, которые требуется решить.
3. Выбор типа модели: определение, какой тип модели (аналитическая, численная, статистическая и т.д.) будет использоваться для описания системы.
4. Создание математической модели: разработка уравнений и отношений, которые описывают взаимодействие компонентов системы.
5. Верификация и валидация модели: проверка правильности моделирования и соответствия результатов модели реальным данным или наблюдениям.
6. Анализ и интерпретация результатов: изучение и анализ полученных результатов моделирования для понимания поведения и свойств системы.
7. Применение модели: использование модели для прогнозирования, оптимизации, принятия решений или других практических целей.

Математическое моделирование позволяет упростить и абстрагировать сложные системы, выявить их основные свойства и закономерности, а также предсказать и оптимизировать их поведение. Это мощный инструмент для исследования и улучшения реальных систем и процессов.

Роли и задачи математического моделирования

Математическое моделирование играет важную роль в различных областях науки и техники. Оно позволяет описать и изучить сложные системы, которые невозможно анализировать аналитически или экспериментально. Основная задача математического моделирования заключается в создании математических моделей, которые могут быть использованы для предсказания поведения исследуемой системы, а также для оптимизации и улучшения ее параметров.

Роль математического моделирования заключается в том, чтобы помочь ученым и инженерам понять сложные явления и процессы, которые происходят в мире. Оно позволяет предсказывать результаты экспериментов, проводить виртуальные испытания и оптимизировать процессы для достижения лучших результатов. Математическое моделирование также позволяет проводить исследования и тестирование различных гипотез, что помогает ученым развивать новые теории и концепции.

Задачи математического моделирования могут быть разнообразными и зависят от конкретной области применения. Например, в физике моделирование может использоваться для описания движения тела или взаимодействия физических полей. В экологии математические модели могут помочь предсказать изменения в популяции животных или растений в зависимости от экологических условий. В экономике моделирование может использоваться для прогнозирования экономических показателей и разработки стратегий управления.

Однако, независимо от области применения, задачи математического моделирования включают в себя следующие основные этапы: выбор и постановка задачи, разработка математической модели, ее анализ и решение, интерпретация результатов и проверка модели экспериментальными данными. Каждый из этих этапов требует использования различных математических методов и подходов, а также специальных программных средств и компьютерных технологий.

В целом, математическое моделирование является мощным инструментом для изучения сложных систем и предсказания их поведения. Оно позволяет ученым и инженерам получить новые знания, разработать новые технологии и решить ряд актуальных проблем в различных областях науки и техники.

Типы математических моделей

Тип моделиОписание

Аналитическая модель	Модель, которая описывается с помощью аналитических функций и уравнений. Это позволяет проводить точные математические рассуждения и получать аналитические решения.
Статистическая модель	Модель, основанная на статистических данных. Она используется для анализа и прогнозирования вероятностей и распределений величин.
Дискретная модель	Модель, в которой время и значения переменных представлены дискретными (отдельными) значениями. Она используется для моделирования дискретных событий и процессов.
Непрерывная модель	Модель, в которой время и значения переменных представлены непрерывными функциями. Она используется для моделирования непрерывных событий и процессов.
Детерминированная модель	Модель, в которой результаты определяются точно и предсказуемо. Она используется для моделирования систем без случайности.
Вероятностная модель	Модель, в которой результаты определяются с использованием вероятностей и случайных переменных. Она используется для моделирования систем с случайностью.
Системная модель	Модель, которая описывает взаимодействие и связи между различными компонентами системы. Она позволяет изучать влияние изменений в одной части системы на другие части.

Выбор типа математической модели зависит от целей и характера исследования. Важно выбрать подходящую модель для конкретной задачи, чтобы получить достоверные результаты и сделать осмысленные выводы.

Процесс создания математической модели

Первым этапом является формулировка проблемы, в которой определяются цель и задачи моделирования. На этом этапе определяются основные параметры и переменные, которые будут использоваться в модели.

Вторым этапом является сбор и анализ данных. На этом этапе собираются данные о системе, которую необходимо моделировать. Это может быть информация о поведении объекта, его параметрах, внешних воздействиях и других факторах, влияющих на систему.

Третий этап — разработка математической модели. На этом этапе определяются математические уравнения и функции, которые описывают изменение системы во времени и зависимости между переменными.

Четвертый этап — проверка и анализ модели. На этом этапе модель подвергается тестированию и анализу, чтобы убедиться в ее правильности и адекватности. Это может включать в себя сравнение результатов моделирования с реальными данными или сравнение с другими моделями.

Пятый этап — использование модели для прогнозирования и принятия решений. На этом этапе модель используется для прогнозирования поведения системы в различных условиях и принятия решений на основе полученных результатов.

В итоге, процесс создания математической модели включает в себя несколько последовательных шагов, начиная от формулировки проблемы и сбора данных, до разработки модели, ее проверки и использования для прогнозирования и принятия решений.

Методы решения математических моделей

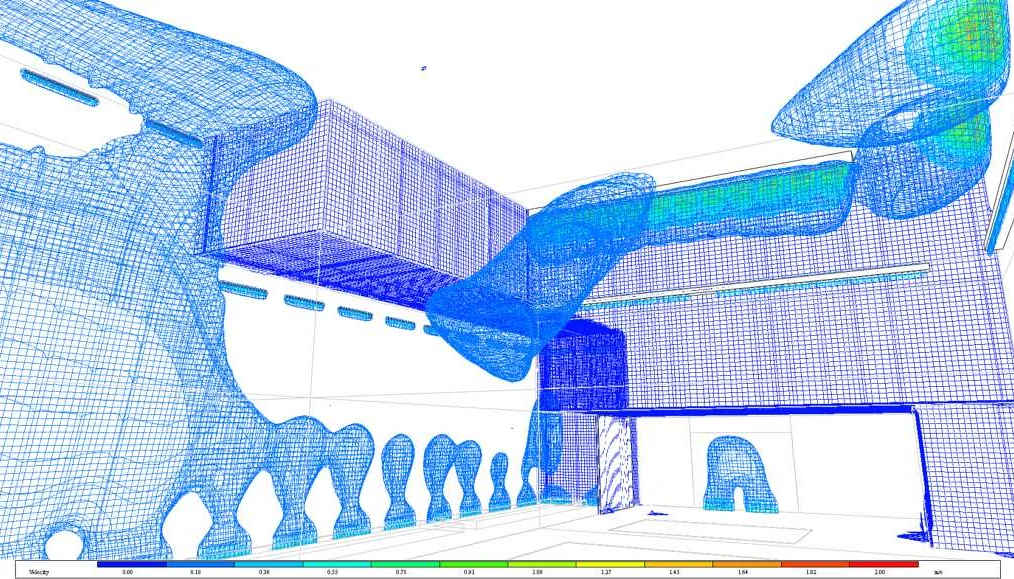
В математическом моделировании существует несколько методов для решения математических моделей. Каждый метод имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи и требований к решению.

Один из наиболее распространенных методов — аналитическое решение. Этот метод основан на использовании математических аналитических формул и выражений для нахождения точного решения модели. Однако, такой метод может быть применен только в случаях, когда модель имеет аналитическое решение. В противном случае, необходимо использовать другие методы.

Другой метод — численное решение. Он заключается в приближенном нахождении решения математической модели путем использования численных методов. Численные методы могут быть дифференциальными, алгебраическими или комбинированными. Они позволяют получить приближенное решение с заданной точностью, однако требуют больше времени и ресурсов для вычислений.

Еще один метод — итерационное решение. Он используется для нахождения решений нелинейных математических моделей, которые не могут быть решены аналитически. Итерационные методы основаны на последовательном приближении к решению путем итераций. Этот процесс повторяется до достижения заданной точности.

Также в математическом моделировании могут применяться вероятностные методы, оптимизационные методы, статистические методы и другие. Выбор метода решения зависит от конкретной задачи, условий и требований.

Применение математического моделирования в разных областях

Применение математического моделирования широко распространено во многих областях, включая физику, экономику, биологию, медицину, инженерию и социальные науки. В физике, например, математическое моделирование позволяет исследовать поведение физических систем, таких как движение тел и распространение волн. В экономике, математическое моделирование может быть использовано для анализа рыночных процессов, определения оптимальных стратегий и прогнозирования будущих трендов.

В биологии и медицине, математическое моделирование используется для изучения биологических систем, таких как рост и развитие популяций, распространение заболеваний и эволюция. Оно помогает предсказывать результаты клинических испытаний, оптимизировать дозировку лекарств и разрабатывать новые методы лечения.

В инженерии, математическое моделирование применяется для проектирования и оптимизации различных систем, таких как транспортные сети, энергетические системы и производственные процессы. Оно позволяет проводить виртуальные испытания и эксперименты, что ускоряет процесс разработки и снижает затраты.

В социальных науках, математическое моделирование используется для изучения социальных явлений и общественных систем. Оно позволяет моделировать процессы принятия решений, социальные взаимодействия и поведение групп людей. Это может помочь в прогнозировании результатов политических выборов, определении оптимальных стратегий поведения и понимании динамики социальных сетей.

В заключение, математическое моделирование играет важную роль во многих областях знаний. Оно помогает улучшить понимание явлений и процессов, предсказывать результаты и оптимизировать системы. Применение математического моделирования продолжает расширяться и развиваться, открывая новые возможности для научных исследований и приложений в реальном мире.

Преимущества и ограничения математического моделирования

Одним из основных преимуществ математического моделирования является его способность предсказывать результаты экспериментов или наблюдений, которые еще не были проведены. Моделируя систему, мы можем проанализировать различные варианты и выбрать наиболее оптимальный или предсказать возможные последствия изменений в системе.

Математическое моделирование также позволяет проводить исследования в условиях, которые в реальности являются непрактичными или невозможными. Например, моделирование позволяет изучать поведение гигантских систем, таких как планеты или галактики, или прогнозировать изменения в климате на глобальном уровне.

Однако, у математического моделирования есть и свои ограничения. Во-первых, любая модель является упрощением реальности и не может учесть все факторы, которые могут влиять на систему. Например, при моделировании погоды невозможно учесть все воздействия, такие как ветер, влажность, атмосферное давление и т.д.

Во-вторых, математическое моделирование требует точных данных и параметров для создания реалистичных моделей. Ошибки или неточности в данных могут привести к неправильным результатам и неверным выводам.

Также, математическое моделирование не всегда может учесть неопределенность и случайность, которые могут быть присутствовать в системе. Неконтролируемые факторы или случайные события могут привести к отклонениям от прогнозов модели и созданию непредвиденных результатов.

В целом, математическое моделирование является полезным инструментом для изучения и анализа систем, однако необходимо учитывать его ограничения и быть внимательным при интерпретации результатов.

Вопрос-ответ:

Что такое математическое моделирование?

Математическое моделирование — это процесс создания математической модели, которая описывает поведение системы или явления в виде математических уравнений и формул.

Какие принципы лежат в основе математического моделирования?

Основными принципами математического моделирования являются абстракция, упрощение, аппроксимация и верификация. Абстракция позволяет выделить главные характеристики системы и игнорировать незначительные детали. Упрощение упрощает математическую модель, чтобы сделать ее решение более доступным. Аппроксимация представляет систему или явление с помощью приближенных математических выражений. Верификация — это проверка правильности математической модели.

Какие области применения математического моделирования?

Математическое моделирование применяется во многих научных областях, включая физику, химию, биологию, экономику, социологию и технику. Оно используется для предсказания поведения систем и явлений, для оптимизации процессов и принятия решений, а также для проведения научных исследований и экспериментов.

Какие методы применяются в математическом моделировании?

В математическом моделировании применяются различные методы и подходы, включая дифференциальные уравнения, разностные уравнения, стохастические модели, оптимизацию, статистический анализ и многое другое. Выбор метода зависит от конкретной задачи и требуемой точности моделирования.

Каковы преимущества использования математического моделирования?

Использование математического моделирования позволяет получить более глубокое понимание систем и явлений, предсказывать их будущее поведение, оптимизировать процессы и принимать обоснованные решения. Оно также позволяет проводить виртуальные эксперименты, что может быть более безопасным, дешевым и эффективным, чем реальные эксперименты.

Видео по теме: