Что такое в математике отношения проценты пропорции
Содержимое
- 1 Что такое в математике отношения проценты пропорции
- 1.1 Что такое отношение в математике?
- 1.2 Как работать с процентами?
- 1.3 Пропорции: что это и как их использовать?
- 1.4 Отношения и проценты: практические примеры
- 1.5 Пропорции в реальной жизни: как применять?
- 1.6 Отношения и проценты в финансах и экономике
- 1.7 Пропорции и геометрия: как связаны?
- 1.8 Отношения, проценты и пропорции в статистике и анализе данных
- 1.9 Вопрос-ответ:
- 1.10 Видео по теме:
Статья расскажет о том, что такое отношения, проценты и пропорции в математике. Вы узнаете, как они связаны между собой и как применять их в решении задач.
Математика — это наука, которая изучает различные аспекты количества, пространства, структуры и изменения. Одним из важных понятий в математике являются отношения. Они основаны на сравнении двух или более величин и выражаются с помощью математических символов, таких как «=», «>», »
Проценты — еще одно важное понятие в математике. Проценты используются для измерения доли или части от целого. Обычно они выражаются в виде десятичных дробей, умноженных на 100. Например, 50% означает половину от целого, а 75% — три четверти. Проценты широко используются в финансовых расчетах, статистике и других областях, где важно выразить долю или изменение величины.
Пропорции — это математическое понятие, которое выражает равенство двух отношений. Оно позволяет сравнивать и анализировать величины и их соотношения. Пропорции могут быть представлены в виде уравнений, где две пары отношений равны друг другу. Например, если 4 яблока стоят 8 долларов, то 6 яблок будут стоить 12 долларов. Пропорции используются во многих областях, включая геометрию, физику, экономику и торговлю.
Понимание отношений, процентов и пропорций является важным элементом не только в математике, но и в повседневной жизни. Эти концепции позволяют нам анализировать и сравнивать данные, прогнозировать результаты и принимать обоснованные решения. Научиться применять эти понятия в реальных ситуациях поможет не только лучше понять мир вокруг нас, но и развить навыки критического мышления и логического рассуждения.
Что такое отношение в математике?
Отношение может быть представлено в виде дроби, где числитель — это количество или величина, с которой устанавливается связь, а знаменатель — это количество или величина, с которой связь устанавливается.
Отношение может быть выражено также в виде процента, который показывает, какую часть одной величины составляет другая величина.
Отношения могут быть прямыми или обратными. Прямое отношение означает, что с увеличением одной величины, другая величина также увеличивается. Обратное отношение означает, что с увеличением одной величины, другая величина уменьшается.
Отношения могут быть также пропорциональными или непропорциональными. Пропорциональные отношения означают, что две величины изменяются в одинаковой пропорции. Непропорциональные отношения означают, что две величины не изменяются в одинаковой пропорции.
Отношения используются для решения различных задач и задач в математике, физике, экономике и других науках. Они помогают нам понять и описать взаимосвязи между различными явлениями и явлениями в реальном мире.
Вид отношенияПример
| Прямое отношение | Чем больше времени, проведенного на учебу, тем лучше результаты |
| Обратное отношение | Чем больше расстояние, тем меньше скорость |
| Пропорциональное отношение | Чем больше количество работников, тем больше продукция |
| Непропорциональное отношение | Чем больше скорость автомобиля, тем больше расход топлива |
Как работать с процентами?
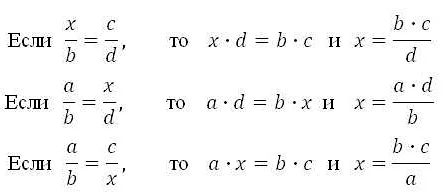
Процент – это доля от целого, выраженная в сотых долях. Обычно проценты обозначаются знаком % и помещаются после числа. Например, 10% означает 10 сотых долей или 10/100, что эквивалентно 0.1.
Есть несколько способов работы с процентами. Один из них – нахождение процента от числа. Для этого необходимо умножить число на процент и разделить на 100. Например, если нужно найти 20% от числа 80, то мы умножаем 80 на 20 и делим на 100: 80 * 20 / 100 = 16.
Другой способ работы с процентами – нахождение числа, соответствующего определенному проценту. Для этого необходимо умножить число на 100 и разделить на процент. Например, если известно, что 40 является 25% от искомого числа, то мы умножаем 40 на 100 и делим на 25: 40 * 100 / 25 = 160.
Также можно решать задачи, связанные с изменением числа на определенный процент. Для этого нужно умножить число на 1 плюс процент (в десятичной форме). Например, если необходимо увеличить число 50 на 30%, то мы умножаем 50 на 1 плюс 0.3: 50 * (1 + 0.3) = 65.
Зная основные правила и методы работы с процентами, можно успешно решать различные задачи, связанные с финансами, экономикой и другими областями. Помните, что практика – лучший способ закрепить знания и стать уверенным в работе с процентами.
Пропорции: что это и как их использовать?
Пропорции широко используются в различных областях, включая финансы, науку, технику и торговлю. Они помогают решать задачи, связанные с расчетами процентов, долей, отношений и других важных параметров.
Для использования пропорций необходимо знать основные правила и методы. Во-первых, необходимо составить пропорцию, где каждая пара величин будет располагаться по одному и тому же правилу. Например:
- 4 : 8 = 6 : 12
- 3/4 : 2/3 = 5/6 : x
После составления пропорции можно решить ее, используя различные методы, такие как метод средних пропорций или метод формулы.
Применение пропорций может быть полезно во множестве ситуаций. Например, с их помощью можно рассчитать процентное соотношение скидки на товар, распределить доли в смеси различных веществ или определить соотношение между двумя числами.
В заключение, пропорции являются важным инструментом в математике и широко используются для решения различных задач. Понимание понятия пропорций и умение их применять поможет вам в решении различных математических задач и повседневных проблем.
Отношения и проценты: практические примеры
Проценты используются для измерения доли или части от общего целого. Например, если у вас есть 100 яблок, и 30 из них зеленые, то вы можете сказать, что доля зеленых яблок составляет 30% от общего количества яблок.
Давайте рассмотрим пример отношения. Представьте, что в вашем классе 20 мальчиков и 30 девочек. Вы можете выразить это отношение как 20:30 или упростить его до 2:3. Это означает, что на каждых 2 мальчиков приходится 3 девочки.
Еще один практический пример — расчет налога на товары и услуги (НДС). Предположим, что вы купили товар стоимостью 1000 рублей, и на товар действует НДС в размере 20%. Чтобы узнать, сколько вы заплатите в качестве налога, вы можете умножить стоимость товара на процент НДС: 1000 * 0.20 = 200 рублей. Таким образом, сумма налога составляет 200 рублей.
Отношения и проценты широко применяются в бизнесе, финансах, экономике и других сферах жизни. Понимание этих понятий позволяет нам анализировать данные, сравнивать их и принимать обоснованные решения.
В заключение, отношения и проценты являются важными инструментами в математике, которые помогают нам измерять и анализировать соотношения между величинами. Практические примеры, такие как доли, проценты налогов и отношения чисел, помогают нам лучше понять и применять эти понятия в реальной жизни.
Пропорции в реальной жизни: как применять?

- Торговля и экономика: Пропорции могут быть полезны для расчета скидок и наценок. Например, если товар продается со скидкой 20%, можно использовать пропорцию для определения конечной цены.
- Кулинария: Пропорции помогут вам правильно сбалансировать ингредиенты и приготовить блюдо нужного размера. Например, если рецепт указывает на использование 2 столовых ложек сахара для 4 порций, можно использовать пропорцию для определения количества сахара для другого количества порций.
- Строительство: Пропорции широко используются в строительстве для планирования и расчета размеров объектов. Например, пропорции могут быть использованы для определения высоты строения относительно его ширины или длины.
- Картография: Пропорции применяются при создании карт для обеспечения точного масштабирования и отображения действительных размеров территории.
Это всего лишь несколько примеров, где пропорции могут быть использованы в реальной жизни. Понимание и применение пропорций позволяет нам более точно анализировать и решать различные задачи, основанные на отношениях и соотношениях.
Отношения и проценты в финансах и экономике
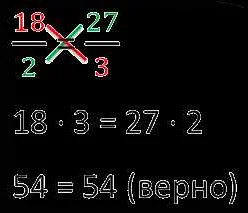
Отношения и проценты играют важную роль в финансах и экономике. Они позволяют оценить и анализировать различные аспекты деятельности компаний, инвестиций, потребительского спроса и других экономических явлений.
Процентные ставки являются одним из основных инструментов денежно-кредитной политики центральных банков. Изменение процентных ставок влияет на спрос на кредиты, инвестиционную активность и уровень инфляции.
Проценты также играют важную роль в финансовых инвестициях. Различные финансовые инструменты, такие как облигации, депозиты и акции, могут приносить доходы в виде процентов. Инвесторы могут использовать процентные ставки и отношения для оценки доходности инвестиций.
Отношения также имеют свое применение в финансовой аналитике. Например, отношение текущих активов к текущим обязательствам позволяет оценить финансовую устойчивость компании и ее способность погасить текущие долги.
Кроме того, отношения и проценты используются в экономической статистике для анализа и прогнозирования экономических показателей. Например, отношение инвестиций к ВВП позволяет оценить уровень инвестиционной активности в экономике.
- Процентные ставки являются инструментом денежно-кредитной политики центральных банков.
- Финансовые инвестиции могут приносить доходы в виде процентов.
- Отношения используются для оценки финансовой устойчивости компаний.
- Отношения и проценты используются в экономической статистике для анализа экономических показателей.
Пропорции и геометрия: как связаны?
В геометрии, пропорции используются для выражения отношений между сторонами или измерениями фигур. Например, в треугольнике пропорция может быть использована для определения отношения между длинами его сторон. Если стороны треугольника образуют пропорцию, то это означает, что соответствующие стороны имеют одинаковое отношение.
Пропорции также могут быть использованы для изучения подобия геометрических фигур. Две фигуры считаются подобными, если их соответствующие стороны образуют пропорцию. Например, если стороны одного треугольника имеют отношение 2:1 по сравнению с соответствующими сторонами другого треугольника, то эти треугольники считаются подобными.
Пропорции могут быть также использованы для нахождения неизвестных значений или измерений в геометрии. Например, если известно, что две пропорциональные стороны треугольника имеют отношение 3:5, то можно использовать пропорцию для нахождения значения третьей стороны.
Таким образом, пропорции являются важным инструментом в геометрии, позволяющим выражать отношения и связи между геометрическими объектами и измерениями. Они играют важную роль в решении задач и анализе геометрических фигур.
Отношения, проценты и пропорции в статистике и анализе данных

В статистике и анализе данных отношения, проценты и пропорции играют важную роль. Они помогают оценить различные характеристики и закономерности в данных.
Отношение — это сравнение двух чисел или величин. Оно может быть выражено в виде доли, десятичной дроби или процента. Например, отношение мужчин к женщинам в определенной группе может быть выражено как 2:3 или 40%:60%.
Процент — это специальный вид отношения, выраженный в виде сотых долей. Он позволяет выразить одно значение относительно другого в процентном соотношении. Например, если в опросе 70% опрошенных ответили положительно, то это означает, что 70 из 100 опрошенных дали положительный ответ.
Пропорция — это отношение двух частей или групп величин. Она позволяет сравнить долю одной группы с долей другой группы. Пропорция может быть выражена в виде доли или процента. Например, если 80% студентов в классе получили высокую оценку, а 20% получили низкую оценку, то можно сказать, что пропорция студентов, получивших высокую оценку, к студентам, получившим низкую оценку, составляет 4:1.
Отношения, проценты и пропорции используются в статистике и анализе данных для определения различных параметров и трендов. Например, они могут быть использованы для анализа соотношения мужчин и женщин в определенной группе, оценки процента успеха или неудачи в определенной области и сравнения доли покупателей разных товаров.
Важно уметь правильно интерпретировать и использовать отношения, проценты и пропорции в статистике и анализе данных, так как они могут помочь принять правильные решения на основе полученных результатов.
Вопрос-ответ:
Какие понятия связаны с отношениями в математике?
Отношения в математике связаны с понятиями сравнения, эквивалентности и пропорциональности. Отношение может быть задано как сравнением двух величин или как соотношением между частями и целым.
Каким образом проценты используются в математике?
Проценты широко используются в математике для выражения долей и отношений. Они позволяют выразить одну величину в процентах от другой и использовать их для решения задач связанных с прибылью, процентными ставками и т.д.
Какие примеры можно привести для процентов в математике?
Примеры использования процентов в математике: расчет скидок в магазине, определение налоговой ставки, вычисление прироста или убытка в бизнесе, расчет процентной ставки по кредиту и многое другое.
Как определить пропорциональность в математике?
Пропорциональность в математике можно определить, сравнивая коэффициенты пропорциональности. Если они равны, то величины пропорциональны. Также можно использовать пропорцию, где отношение двух величин равно отношению других двух величин.
Какие примеры можно привести для пропорций в математике?
Примеры использования пропорций в математике: расчет скорости, определение площади подобных фигур, расчет времени, необходимого для выполнения работы, и многое другое.
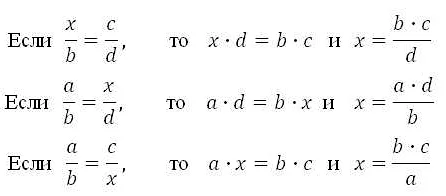



Очень интересная и познавательная статья! Я всегда была слаба в математике, поэтому мне действительно пригодилось разъяснение этих понятий. Теперь я наконец понимаю, что такое отношения, проценты и пропорции, и как они применяются в реальной жизни. Примеры из статьи помогли мне лучше усвоить материал. Теперь я вижу, что эти понятия встречаются повсюду: в финансах, экономике, на работе, даже в повседневных задачах. Спасибо автору за понятное изложение материала и за помощь в освоении математики! Теперь я не так боюсь сталкиваться с этими понятиями в реальной жизни.