Что такое плоскости математического горизонта

Плоскости математического горизонта — это понятие, которое используется в математике для описания геометрического пространства. Они представляют собой плоскости, параллельные горизонтальной плоскости, которая является основной базовой плоскостью в системе координат. Понимание плоскостей математического горизонта важно для решения различных задач в математике и других науках.

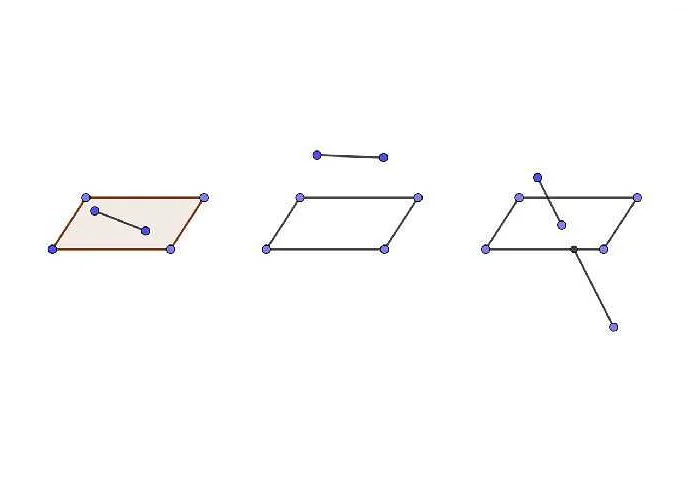
В математике понятие плоскости является одним из основных элементов геометрии. Плоскость представляет собой двумерное геометрическое пространство, не имеющее толщины и ограниченное бесконечным количеством прямых линий. Она является абстрактным объектом, который можно представить в виде бесконечной прямой поверхности.

Плоскости математического горизонта играют важную роль в различных областях математики и физики. Они используются для решения задач, связанных с геометрией, алгеброй, механикой и другими науками. Плоскости математического горизонта могут быть горизонтальными, вертикальными или наклонными, в зависимости от их положения относительно горизонтальной и вертикальной осей.

Например, плоскость математического горизонта может быть использована для моделирования поверхности земли или моря, где каждая точка на плоскости соответствует определенной координате в трехмерном пространстве. Это позволяет нам изучать различные геометрические свойства и применять их в практических задачах, таких как навигация, картография и геодезия.

Возможность использования плоскостей математического горизонта для анализа и решения сложных задач делает их важным инструментом для математиков, физиков и инженеров. Они позволяют нам лучше понять и описать физические явления и создавать математические модели, которые могут применяться в различных областях науки и техники.

Плоскости математического горизонта: определение и примеры

Плоскости математического горизонта широко используются для решения различных задач и в различных областях, таких как геометрия, физика, инженерия и информатика. Они позволяют представлять и анализировать различные объекты и явления в двухмерном пространстве.

Примеры плоскостей математического горизонта включают:

• Плоскость координат – это плоскость, на которой оси x и y пересекаются в начале координат. Она используется для задания и изучения различных геометрических фигур и функций.
• Плоскость отображения – это плоскость, на которой проектируются трехмерные объекты для создания двухмерных изображений. Например, в компьютерной графике используется плоскость отображения для рендеринга трехмерных моделей на плоский экран.
• Плоскость горизонта – это плоскость, которая является горизонтальной плоскостью, параллельной горизонту земли. Она используется в геодезии и навигации для определения направления и ориентации объектов в пространстве.

Определение и использование плоскостей математического горизонта играют важную роль в различных математических и научных дисциплинах, обеспечивая удобство и точность в анализе и моделировании объектов и явлений.

Видео по теме:

Определение плоскостей математического горизонта

Плоскости математического горизонта можно представить как бесконечно расширяющиеся горизонты, на которых можно строить геометрические объекты и проводить различные операции. Они не имеют конкретного размера или формы, они простираются бесконечно во всех направлениях.

Примером плоскости математического горизонта может служить плоскость координат, которая используется для задания точек и решения уравнений. В этой плоскости горизонтальная ось X и вертикальная ось Y образуют пересекающиеся линии, которые определяют координаты точек.

Также плоскости математического горизонта могут быть использованы для представления поверхностей, графиков функций и других геометрических объектов. Они позволяют нам анализировать и визуализировать математические концепции и решать различные задачи.

Важно понимать, что плоскости математического горизонта являются абстрактными объектами и существуют только в математическом представлении.

Примеры плоскостей математического горизонта

В математике существует множество примеров плоскостей, которые могут быть использованы в рамках понятия «математический горизонт». Некоторые из них включают:

Плоскость XY: Это наиболее простой пример плоскости, которая является горизонтальной и пересекает оси координат X и Y под прямым углом. Она представляет собой плоскость, на которой можно представить двумерные графики и изображения.

Плоскость XZ: Это еще один пример плоскости, которая является вертикальной и пересекает оси координат X и Z под прямым углом. Она используется для представления двумерных проекций трехмерных объектов.

Плоскость YZ: Это третий пример плоскости, которая является вертикальной и пересекает оси координат Y и Z под прямым углом. Она также используется для представления двумерных проекций трехмерных объектов.

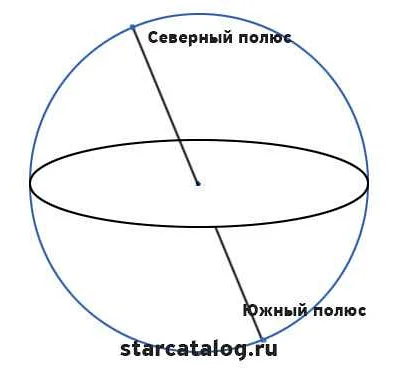
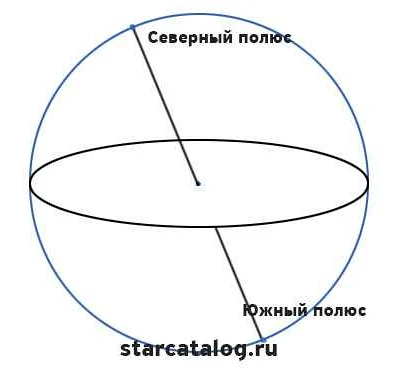
Экватор: Это плоскость, которая делит сферу пополам и проходит через ее центр. Она используется для примера плоскости, которая пересекает трехмерный пространственный объект, такой как сфера.

Плоскость аффинных координат: Это плоскость, которая используется в аффинной геометрии для определения координат точек в пространстве. Она имеет три оси (X, Y, Z) и используется для описания трехмерных объектов.

Это лишь несколько примеров плоскостей, которые могут быть использованы в контексте математического горизонта. В математике существует множество других типов плоскостей, каждая из которых имеет свои особенности и применения.

Вопрос-ответ:

Что такое плоскости математического горизонта?

Плоскости математического горизонта — это плоские поверхности, которые перпендикулярны вертикальной оси и параллельны горизонтальной плоскости. Они используются в геометрии и механике для моделирования движения объектов в трехмерном пространстве.

Какие примеры плоскостей математического горизонта можно привести?

Примерами плоскостей математического горизонта могут служить горизонтальная плоскость, плоскости, проходящие через различные высоты над землей, или плоскости, которые пересекаются с вертикальной осью в разных точках.

Зачем нужны плоскости математического горизонта?

Плоскости математического горизонта используются для упрощения анализа и моделирования движения объектов в трехмерном пространстве. Они позволяют определить положение объекта относительно горизонта и вертикальной оси, что помогает в решении задач геометрии и механики.

Как можно представить плоскости математического горизонта графически?

Плоскости математического горизонта можно представить графически в виде плоских поверхностей, параллельных горизонтальной плоскости и перпендикулярных вертикальной оси. Они могут быть изображены на графиках или чертежах, чтобы показать положение объектов в трехмерном пространстве.

Какие свойства имеют плоскости математического горизонта?

Плоскости математического горизонта обладают несколькими свойствами. Они перпендикулярны вертикальной оси и параллельны горизонтальной плоскости. Они также могут иметь различные высоты над землей, что позволяет моделировать объекты в трехмерном пространстве.

Что такое плоскости математического горизонта?

Плоскости математического горизонта — это плоские поверхности, которые параллельны горизонту и используются в геометрии и физике для описания пространства и его различных характеристик.

Плоскости в геометрии

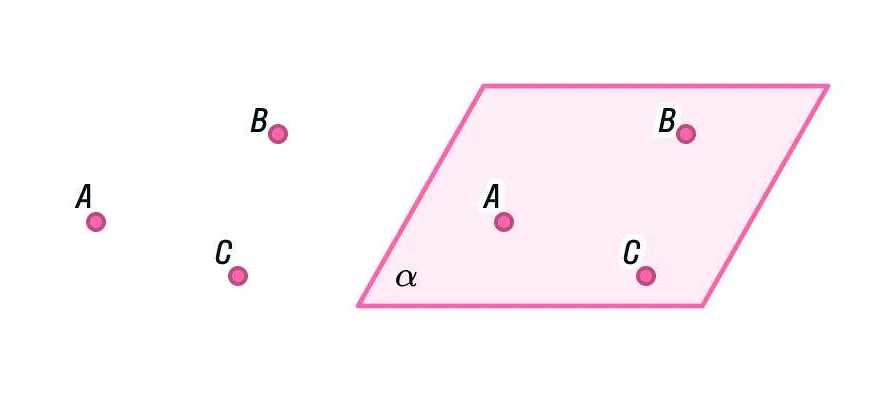
Плоскость также определяется точкой и нормалью. Точка указывает положение плоскости в пространстве, а нормаль — направление, в котором плоскость расположена.

Примерами плоскостей в геометрии могут служить плоскость земли, поверхность стола или стены. Все они являются плоскими поверхностями, которые можно описать горизонтальной и вертикальной геометрическими осями.

Плоскости в физике

В физике понятие плоскости также имеет важное значение и используется для описания различных физических явлений и законов.

В классической механике, плоскости часто используются для описания движения тел. Например, при анализе движения тела, можно представить его движение как движение в плоскости, что позволяет значительно упростить математическую модель и решить уравнения движения.

Плоскости также широко используются в оптике. Например, плоское зеркало представляет собой плоскую поверхность, на которой происходит отражение света. Также плоскости используются при описании интерференции и дифракции света.

В электромагнетизме, плоскости используются для описания электромагнитных волн. С помощью плоскостей можно описать направление распространения волны и поляризацию.

В общем виде, плоскости могут быть использованы для моделирования и описания различных физических процессов и явлений. Они позволяют упростить математическую модель и сделать анализ более наглядным и понятным.

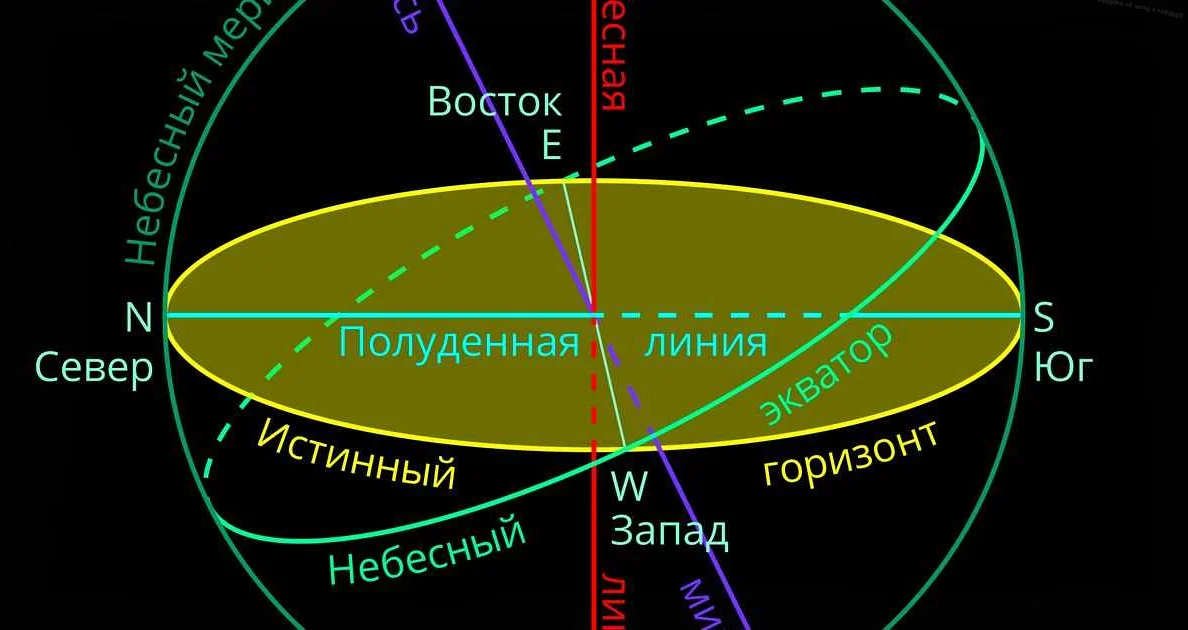
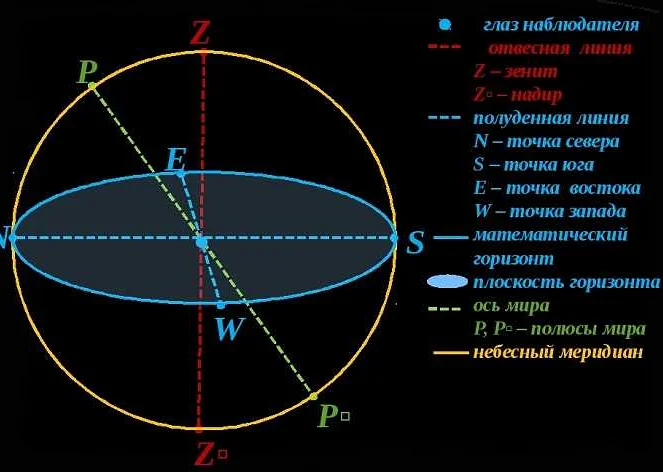
Плоскости в астрономии

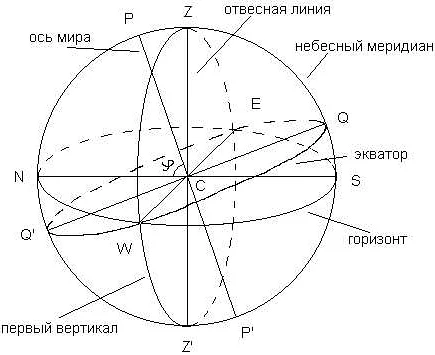
В астрономии существует несколько важных плоскостей, которые используются для описания движения и положения небесных объектов. Эти плоскости помогают упростить астрономические расчеты и обозначить определенные направления в космосе. Вот некоторые из них:

1. Экваториальная плоскость: это плоскость, параллельная земному экватору. Она используется для определения положения звезд и других небесных объектов.
2. Эклиптическая плоскость: это плоскость, которая проходит через Землю и орбиту Земли вокруг Солнца. Она используется для обозначения планет и других объектов Солнечной системы.
3. Галактическая плоскость: это плоскость, которая проходит через центр нашей Галактики (Млечный путь). Она используется для описания расположения звезд и других объектов в нашей Галактике.
4. Супергалактическая плоскость: это плоскость, проходящая через центр локальной супергалактики. Она используется для описания расположения групп галактик и других объектов в более крупных масштабах.

Каждая из этих плоскостей имеет свои особенности и применяется в различных астрономических задачах. Знание и понимание этих плоскостей помогает астрономам исследовать и описывать нашу Вселенную.

Плоскости в архитектуре

В архитектуре плоскости могут быть горизонтальными, вертикальными или наклонными. Горизонтальные плоскости, такие как полы и потолки, определяют границы помещений и создают ощущение пространства. Вертикальные плоскости, такие как стены, разделяют пространство на отдельные комнаты и обеспечивают приватность. Наклонные плоскости, такие как крыши и фасады, придают зданию уникальный внешний вид и защищают его от внешних воздействий.

Плоскости в архитектуре также могут быть использованы для создания интересных визуальных эффектов. Например, с помощью перекрывающихся плоскостей можно создать объемные формы и играть с пространством. Комбинация разных типов плоскостей может создавать сильные контрасты и придавать зданию динамику.

Плоскости в архитектуре могут быть выполнены из различных материалов, таких как бетон, стекло, камень или металл. Выбор материала зависит от функциональных и эстетических требований здания, а также от практических соображений, таких как стоимость и доступность.

Примерами плоскостей в архитектуре могут служить фасады зданий, витрины магазинов, стены и перегородки внутри помещений, а также полы и потолки. Каждая плоскость имеет свою функцию и вносит свой вклад в общий облик здания.

Плоскости в компьютерной графике

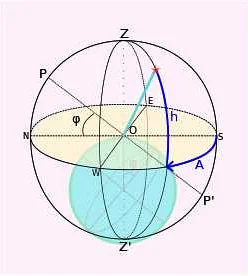
Плоскости в компьютерной графике могут быть использованы для создания различных объектов и эффектов, таких как поверхности, объекты, текстуры и тени. Они описываются с помощью математических уравнений или параметрических формул, которые определяют их форму и положение в трехмерном пространстве.

Одним из примеров использования плоскостей в компьютерной графике является построение трехмерных объектов. Путем комбинирования нескольких плоскостей, можно создать различные формы и объемные модели. Кроме того, плоскости используются для отображения текстур на поверхности объектов, что позволяет придавать им реалистичный вид.

Плоскости также используются для создания эффектов освещения и теней. Путем установки плоскости в определенном положении и применения эффектов света, можно создать реалистичную модель освещения объектов. Тени также реализуются с помощью плоскостей, которые отображаются на поверхности других объектов.

Кратко говоря, плоскости в компьютерной графике являются важным инструментом для создания трехмерных изображений и эффектов. Они позволяют моделировать различные формы, отображать текстуры, создавать реалистичные эффекты освещения и теней, что делает изображения более живыми и привлекательными.