Что такое пропорция в математике 7 класс

Пропорция в математике 7 класс — это математическое понятие, которое используется для сравнения двух или более величин, чтобы установить их отношение. В данной статье вы узнаете, как работать с пропорциями и решать задачи на их основе в 7 классе.

Пропорция — одно из важнейших понятий в математике, с которым ученики 7 класса сталкиваются в ходе изучения предмета. Пропорция является основным инструментом для решения различных задач, связанных с соотношениями. Она позволяет определить, какие величины пропорциональны друг другу и как изменение одной величины влияет на другие.

Правила использования пропорции достаточно просты. Они основаны на равенстве долей или отношений двух пар величин. Если у нас есть четыре числа — a, b, c и d, то мы можем сказать, что пропорция верна, если отношение a к b равно отношению c к d. Такое равенство можно записать в виде a:b = c:d или в виде a/b = c/d. Важно помнить, что пропорция может быть правильной или неправильной, в зависимости от выполняющегося условия.

Примером правильной пропорции может служить следующая задача: «Если 4 яблока стоят 120 рублей, сколько стоят 10 яблок?» В этом случае мы можем записать пропорцию 4:120 = 10:x, где х — искомая цена 10 яблок. Путем решения этой пропорции мы можем найти значение х и узнать, сколько стоят 10 яблок.

Изучение пропорции в 7 классе является важным шагом в математическом образовании учеников. Оно помогает развить навыки анализа и решения различных задач, связанных с соотношениями величин. Правильное использование пропорции позволяет ученикам легче осваивать более сложные темы и применять полученные знания на практике.

Что такое пропорция?

Пропорция записывается в виде a:b = c:d, где a и c – первый и второй члены, а b и d – третий и четвертый члены. Первый и второй члены называются антецедентами, а третий и четвертый – консеквентами.

Пропорция может быть прямой или косвенной. В прямой пропорции при увеличении одной величины другая величина также увеличивается. В косвенной пропорции при увеличении одной величины другая величина уменьшается.

Пропорции широко применяются в различных областях, включая геометрию, физику, экономику и т. д. Они помогают решать задачи сравнения, нахождения неизвестных величин и предсказания результатов в различных ситуациях.

Виды пропорций в математике

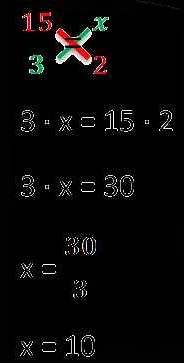
В математике существуют различные виды пропорций, которые используются для решения различных задач. Основные виды пропорций:

НазваниеОписание

Прямая пропорция	Пропорция, в которой при увеличении (уменьшении) одной величины, другая величина также увеличивается (уменьшается) пропорционально.
Обратная пропорция	Пропорция, в которой при увеличении (уменьшении) одной величины, другая величина уменьшается (увеличивается) пропорционально.
Смешанная пропорция	Пропорция, которая является комбинацией прямой и обратной пропорций.

Знание различных видов пропорций позволяет более гибко решать математические задачи, связанные с пропорциональными зависимостями между величинами. Определение типа пропорции помогает выбрать подходящий метод решения и получить правильный ответ.

Основные правила работы с пропорциями

Основные правила работы с пропорциями:

ПравилоОписание

Первое правило	Если две пары чисел образуют пропорцию, то их произведения равны: a * d = b * c.
Второе правило	Если в пропорции одно из отношений равно единице, то другое отношение также равно единице.
Третье правило	Если в пропорции одно из отношений равно нулю, то другое отношение также равно нулю.
Четвертое правило	Если две пропорции равны, то их произведения также равны.

Правила работы с пропорциями позволяют решать различные задачи, связанные с пропорциональными величинами. Зная значения трех величин, можно найти значение четвертой величины, используя пропорцию.

Способы решения пропорций

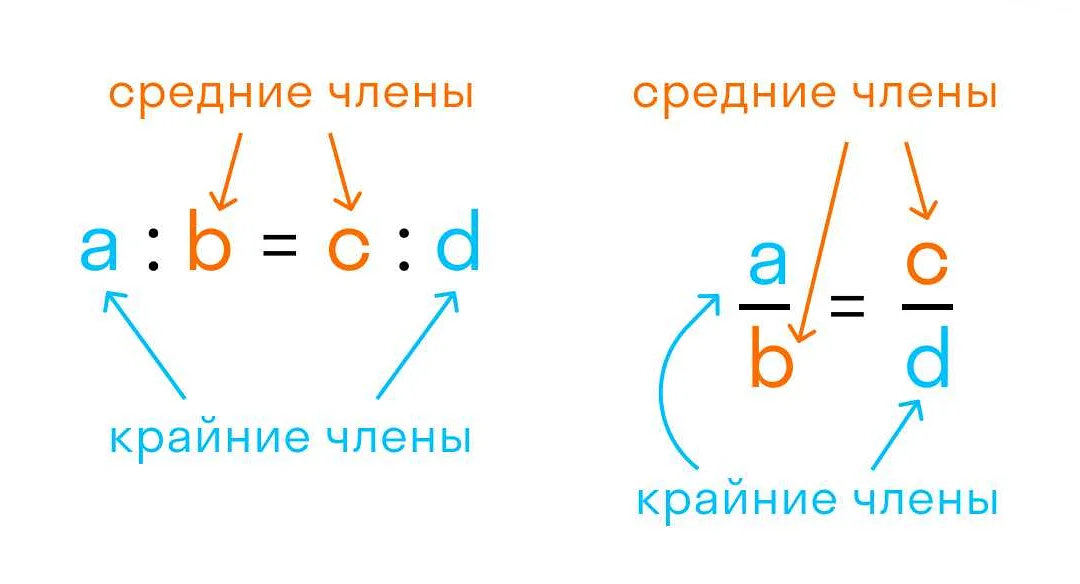
В математике существует несколько способов решения пропорций. Рассмотрим основные из них:

1. Метод равных произведений. Суть этого метода заключается в том, что произведение крайних и средних членов пропорции равно. Для решения пропорции с помощью этого метода необходимо уравнять произведения и найти значение неизвестной величины.

2. Метод перекрестных произведений. Этот метод основан на равенстве произведений крайних и средних членов пропорции. Для его применения необходимо умножить крайние члены пропорции и средние члены пропорции, затем уравнять полученные произведения и найти значение неизвестной.

3. Метод пропорций с одной неизвестной. Этот метод подходит для решения пропорций, в которых известны значения всех величин, кроме одной. Для решения пропорции с помощью этого метода необходимо выразить неизвестную величину через известные значения и затем решить полученное уравнение.

4. Метод подстановки. Этот метод применяется, когда значение одной величины известно, а неизвестное значение нужно найти путем последовательной подстановки различных значений. Путем подстановки проверяются разные значения неизвестной величины, пока не будет найдено значение, удовлетворяющее условию пропорции.

Знание различных способов решения пропорций позволяет выбирать наиболее удобный и эффективный метод в каждом конкретном случае. Важно помнить, что при решении пропорции необходимо учитывать правила математических операций и последовательность их выполнения.

Примеры пропорций и их решение

ПримерРешение

Если 2 яблока стоят 50 рублей, сколько стоят 5 яблок?	Решение данной пропорции можно представить следующим образом: 2 яблока / 50 рублей = 5 яблок / Х рублей Путем перекрестного умножения получаем: 2 * Х рублей = 5 * 50 рублей Х рублей = 250 рублей. Таким образом, 5 яблок стоят 250 рублей.
Если 4 рабочих могут выполнить задание за 6 дней, сколько дней потребуется для выполнения того же задания 8 рабочими?	Решаем данную пропорцию: 4 рабочих / 6 дней = 8 рабочих / Х дней Путем перекрестного умножения получаем: 4 * Х дней = 8 * 6 дней Х дней = 48 дней. Следовательно, 8 рабочих смогут выполнить задание за 48 дней.
Если 3 метра ткани стоят 1200 рублей, сколько стоит 5 метров той же ткани?	Решение данной пропорции: 3 метра / 1200 рублей = 5 метров / Х рублей Путем перекрестного умножения получаем: 3 * Х рублей = 5 * 1200 рублей Х рублей = 2000 рублей. Таким образом, 5 метров ткани стоят 2000 рублей.

Это лишь некоторые из множества примеров, в которых применяются пропорции. Используя правила решения пропорций, вы можете решать различные задачи, связанные с сравнением отношений. Помните, что важно правильно сформулировать пропорцию и последовательно решить ее, чтобы получить верный ответ.

Задачи на пропорциональное деление

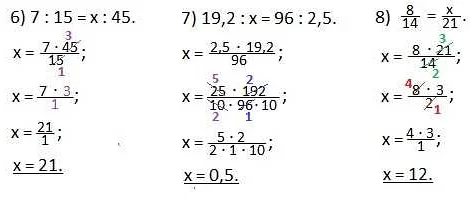
Для решения задач на пропорциональное деление необходимо уметь составлять и анализировать пропорции. Основной прием – перестановка и пересечение долей. Задачи могут быть различной сложности и могут включать несколько этапов решения.

Пример задачи на пропорциональное деление:

Задача: Два рабочих могут выполнить работу за 4 дня. Сколько дней потребуется для выполнения этой работы одному рабочему?

Решение:

Пусть x – количество дней, потребующееся одному рабочему.

Используем пропорцию:

2 рабочих делают работу за 4 дня

1 рабочий делает работу за x дней

Получаем уравнение:

2/4 = 1/x

Переставляем доли:

2x = 4

Находим значение переменной:

x = 4/2 = 2

Ответ: одному рабочему потребуется 2 дня для выполнения работы.

Таким образом, задачи на пропорциональное деление требуют внимательного анализа и правильной постановки пропорции. С помощью пропорций можно решать различные практические задачи, связанные с расчетами и соотношениями между величинами.

Практическое применение пропорции

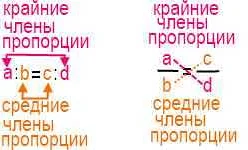
1. Финансы. Пропорция может быть использована для вычисления различных финансовых показателей. Например, для определения стоимости товара в зависимости от его объема или для расчета процентного отношения дохода к расходам.

2. Кулинария. Пропорция может быть полезной при приготовлении пищи. Например, для определения правильного соотношения ингредиентов при рецепте или для изменения количества ингредиентов при изменении объема порций.

3. Архитектура и строительство. Пропорция играет важную роль в архитектуре и строительстве. Она помогает определить соотношение размеров и пропорции различных элементов здания, а также может быть использована для расчета объема материала, необходимого для строительных работ.

4. География. Пропорция может быть использована для измерения расстояний на картах или планах. Она позволяет определить соотношение между физическими объектами и их представлением на плоскости.

5. Медицина. Пропорция может быть полезной в медицинских исследованиях, при определении дозировки лекарств или при проведении клинических испытаний.

Таким образом, пропорция является важным математическим инструментом, который находит применение во многих сферах жизни. Понимание и умение применять пропорцию поможет в решении различных задач и принятии обоснованных решений.

Вопрос-ответ:

Что такое пропорция в математике?

Пропорция — это равенство двух отношений.

Какие правила применяются при работе с пропорциями?

При работе с пропорциями применяются следующие правила: если две пропорции равны, то их обратные пропорции также равны; если в пропорции известны три числа, можно найти четвертое, умножив первое число на четвертое и разделив на второе.

Какие примеры можно привести для объяснения пропорций?

Примеры пропорций: если 2 яблока стоят 20 рублей, то 5 яблок стоят 50 рублей; если 3 рабочих могут выполнить работу за 5 дней, то 6 рабочих смогут выполнить работу за 2.5 дня.

Как решить задачу на пропорцию?

Для решения задачи на пропорцию нужно выразить неизвестное значение через известные значения, затем установить пропорцию и решить уравнение, найдя значение неизвестной величины.

Где в жизни можно применить знание о пропорциях?

Знание о пропорциях может пригодиться в различных ситуациях, например, при расчете стоимости товаров, планировании времени выполнения задач, разделении ресурсов и т.д.

Что такое пропорция в математике?

Пропорция в математике — это равенство двух отношений. В пропорции четыре числа делятся на две пары пропорциональных частей, причем отношение первой пары равно отношению второй пары. Например, если две пары чисел A и B, C и D образуют пропорцию, то отношение A к B равно отношению C к D.

Видео по теме: