Произведение какой знак в математике

Знак произведения в математике — это символ, который обозначает умножение последовательности чисел или выражений. Узнайте, как использовать этот символ и его значения в различных математических контекстах.

Произведение является одним из основных математических операторов, который обозначается символом умножения (×) или точкой (·). Этот знак применяется для обозначения умножения двух чисел или выражений. Произведение позволяет нам определить результат умножения и является одним из фундаментальных понятий в алгебре.

Произведение может быть использовано для умножения чисел, переменных или выражений. Например, если у нас есть два числа — 2 и 3, то их произведение равно 6 (2 × 3 = 6). Также произведение может быть применено к переменным, например, если у нас есть переменные a и b, то их произведение будет представлено выражением ab.

Одной из особенностей произведения является то, что оно обладает коммутативным свойством, то есть порядок умножаемых чисел или выражений не влияет на результат. Например, произведение 2 × 3 будет равно 6, а произведение 3 × 2 также будет равно 6. Это свойство позволяет упростить вычисления и упрощает работу с произведениями в математике.

Произведение имеет широкое применение в различных областях науки и техники. Оно используется для решения различных задач, таких как расчеты в физике, экономике, статистике и других научных и прикладных дисциплинах. Также произведение является основным понятием в алгебре и играет важную роль в построении математических моделей и формулировке законов и теорем.

В заключение, произведение является важным математическим оператором, который позволяет умножать числа и выражения. Оно обладает коммутативным свойством и имеет широкое применение в различных областях науки и техники. Понимание произведения и его особенностей является необходимым для решения различных математических задач и построения математических моделей.

Произведение и его значение в математике

Произведение обычно обозначается с помощью знака умножения «×» или точки «.», и записывается в виде a × b или a · b, где a и b являются множителями. Произведение двух чисел равно числу, полученному при умножении этих чисел.

Произведение может быть использовано для решения различных задач, таких как нахождение площади прямоугольника (где произведение длины и ширины равно площади), вычисление общей стоимости нескольких одинаковых предметов (где произведение цены и количества равно общей стоимости), или нахождение результата возвышения числа в степень (где произведение числа самого с собой столько раз, сколько указано в степени).

Произведение также имеет ряд свойств и особенностей, которые играют важную роль при решении математических задач. Например, произведение двух чисел всегда является коммутативным, то есть a × b = b × a. Кроме того, произведение числа на единицу всегда равно этому числу, то есть a × 1 = a.

В математике произведение также используется для обозначения комбинаторных операций, таких как произведение множеств и произведение перестановок. Эти операции имеют свои собственные правила и свойства, которые позволяют решать различные задачи в комбинаторике и теории вероятностей.

Таким образом, произведение является важным понятием в математике и имеет широкое применение в различных областях этой науки.

Видео по теме:

Произведение: определение и особенности

Произведение обозначается знаком умножения «×» или точкой «.». Например, произведение двух чисел a и b обычно записывается как a × b или a · b.

Основные особенности произведения:

• Коммутативность: порядок множителей не влияет на результат произведения. Для любых чисел a и b выполняется равенство a × b = b × a.
• Ассоциативность: результат произведения не зависит от порядка выполнения операций умножения. Для любых чисел a, b и c выполняется равенство (a × b) × c = a × (b × c).
• Существование нейтрального элемента: единица является нейтральным элементом для произведения. Для любого числа a выполняется равенство a × 1 = 1 × a = a.
• Дистрибутивность: произведение распространяется на сложение. Для любых чисел a, b и c выполняется равенство a × (b + c) = a × b + a × c.

Произведение используется во многих областях математики и ее приложений. Например, оно является основной операцией в алгебре, арифметике, геометрии и др. Оно также широко применяется в физике, экономике, статистике и других науках для моделирования и решения различных задач.

Применение произведения в алгебре

В алгебре произведение играет важную роль при работе с многочленами. Например, при умножении двух многочленов происходит раскрытие скобок и получение нового многочлена, содержащего все возможные произведения между элементами исходных многочленов.

Также произведение используется при решении систем линейных уравнений. При умножении матрицы коэффициентов на вектор неизвестных получается новый вектор, содержащий сумму произведений элементов матрицы и соответствующих элементов вектора неизвестных.

Другой важной областью применения произведения в алгебре является работа с векторами и скалярными произведениями. При вычислении скалярного произведения двух векторов происходит умножение соответствующих элементов векторов и суммирование полученных произведений.

Таким образом, произведение является неотъемлемой частью алгебры и используется для решения различных задач и уравнений. Понимание применения произведения позволяет более эффективно работать с алгебраическими операциями и упрощает процесс решения уравнений и задач.

Вопрос-ответ:

Что такое произведение в математике?

Произведение в математике — это операция, которая позволяет умножать два или более числа, чтобы получить их общее значение.

Как записывается произведение в математике?

Произведение в математике обозначается символом «×» или «*», например, 2 × 3 = 6 или 4 * 5 = 20.

Какие особенности имеет произведение в математике?

Основные особенности произведения в математике: коммутативность (порядок множителей не важен), ассоциативность (порядок операций не важен) и дистрибутивность (произведение распределено относительно сложения и вычитания).

В каких случаях используется произведение в математике?

Произведение в математике используется в различных областях, таких как арифметика, алгебра, геометрия и т. д. Оно применяется для решения уравнений, нахождения площадей, объемов, вероятностей и во многих других математических задачах.

Произведение в геометрии: примеры и свойства

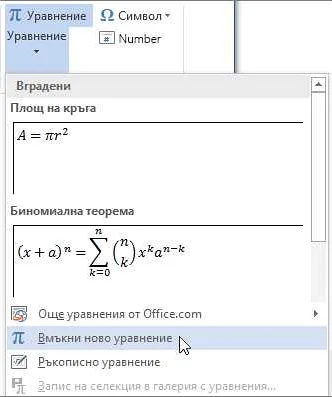
Произведение точек в геометрии может быть определено как пересечение двух прямых или плоскостей. Например, если даны две прямые AB и CD, их произведением является точка E, которая является их пересечением.

Произведение векторов в геометрии определяется как сумма или разность двух векторов. Например, если даны вектор AB и вектор CD, их произведением может быть вектор EF, который является суммой векторов AB и CD.

Произведение в геометрии имеет несколько свойств. Например, произведение точек или векторов не зависит от выбора координатных осей или начальной точки. Кроме того, произведение точек и векторов обладает свойством коммутативности, то есть результат произведения не зависит от порядка операндов.

Произведение в геометрии широко применяется в различных областях, таких как строительство, архитектура, геодезия и многие другие. Например, произведение точек используется для определения пересечений прямых или плоскостей при планировании строительства зданий или дорог. Произведение векторов применяется для определения силы или направления в физике и инженерии.

Произведение в теории вероятностей и статистике

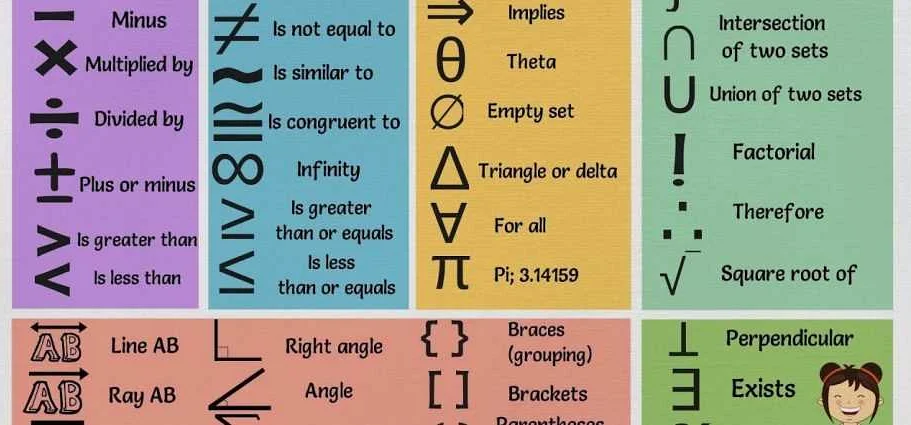
Произведение вероятностей двух событий A и B обозначается как P(A и B) или P(A, B). Для независимых событий, вероятность их произведения равна произведению их вероятностей: P(A и B) = P(A) * P(B).

Произведение вероятностей используется, например, при решении задач на комбинаторику, где требуется рассчитать вероятность одновременного наступления нескольких событий. Также оно применяется при расчете условной вероятности, когда вероятность одного события зависит от наступления другого.

В статистике произведение вероятностей может использоваться для построения моделей и прогнозирования результатов. Например, при анализе данных о покупках в интернет-магазине можно использовать произведение вероятностей отдельных событий (например, вероятность покупки конкретного товара и вероятность его возврата) для оценки общей вероятности совершения покупки.

Важно отметить, что произведение вероятностей может быть использовано только для независимых событий. Если события зависимы, то для расчета вероятности их совместного наступления необходимо использовать другие методы, например, формулу условной вероятности.

Произведение в математическом анализе: интегралы и суммы

Интеграл — это математический объект, который является обобщением понятия площади или объема. Он позволяет рассчитать площадь фигуры на плоскости или объем тела в пространстве путем разбиения фигуры на бесконечно малые элементы и суммирования их площадей или объемов.

Сумма — это алгебраическая операция, которая позволяет складывать числа или другие математические объекты. В математическом анализе сумма используется для аппроксимации интегралов и вычисления их значений. Путем разбиения интеграла на малые промежутки и вычисления сумм площадей фигур на этих промежутках можно получить приближенное значение интеграла.

Интегралы и суммы являются важными инструментами в математическом анализе. Они позволяют решать различные задачи, связанные с вычислением площадей, объемов, а также аппроксимацией функций и нахождением приближенных значений числовых интегралов.

ОперацияОписание

Интеграл	Расчет площади фигуры или объема тела путем суммирования бесконечно малых элементов
Сумма	Алгебраическая операция складывания чисел или других математических объектов

Произведение в математическом анализе играет важную роль и является неотъемлемой частью интегралов и сумм. Оно позволяет решать сложные задачи, связанные с вычислением площадей и объемов, а также аппроксимацией функций и нахождением приближенных значений интегралов.

Произведение в теории чисел: делители и простые числа

Произведение двух чисел a и b обозначается символом «·» или «*», и вычисляется как a * b. Например, произведение чисел 2 и 3 равно 6.

В теории чисел произведение имеет свои особенности. Рассмотрим делители числа. Делитель — это число, на которое заданное число делится без остатка. Если a делится на b без остатка, то говорят, что b является делителем a.

Произведение двух чисел может иметь различное количество делителей. Например, произведение чисел 2 и 3 равно 6. Делителями числа 6 являются 1, 2, 3 и 6. То есть, произведение 2 * 3 имеет 4 делителя.

Кроме того, произведение чисел может быть связано с понятием простых чисел. Простые числа — это числа, которые имеют только два делителя: 1 и само число. Например, числа 2, 3, 5, 7 являются простыми числами.

Если произведение двух простых чисел является простым числом, то говорят, что эти числа образуют пару простых чисел. Например, произведение чисел 2 и 3 равно 6, которое не является простым числом. Таким образом, числа 2 и 3 не образуют пару простых чисел.

Изучение произведения в теории чисел позволяет лучше понять свойства чисел, их делители и простые числа. Это важное понятие, которое находит применение в различных областях математики и естественных наук.

Произведение и его связь с другими математическими операциями

Произведение тесно связано с другими математическими операциями. Например, оно обладает свойством коммутативности, то есть порядок перемножаемых чисел не влияет на результат: a × b = b × a. Также произведение обладает свойством ассоциативности: (a × b) × c = a × (b × c).

Произведение можно использовать для решения различных задач и проблем. Например, оно может быть использовано для нахождения площади прямоугольника или квадрата, где произведение длины и ширины равно площади. Также произведение может быть использовано для нахождения общего количества предметов или числа, если известно их количество и количество групп или наборов.

Использование произведения в математике расширяется и на другие области, такие как алгебра, геометрия, физика и экономика. Например, в алгебре произведение матриц используется для решения систем линейных уравнений, а в экономике — для расчета общей стоимости или дохода.