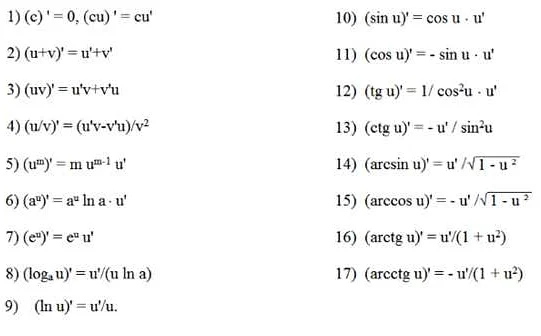Какая буква обозначает производительность в математике: ответ на вопрос

Буква P обозначает производительность в математике. Узнайте, как она используется и расшифровывается в различных областях науки и техники.

В математике производительность — это показатель, указывающий на скорость изменения одной величины относительно другой. В других областях производительность может означать что-то другое, например, скорость производства товаров или услуг. Однако, на этот раз мы рассмотрим термин производительности в математике.

Для обозначения производительности существует специальный математический символ. Этот символ называется производной и обозначается буквой «d» в некоторой степени, за которой следует функция, от которой берется производная, например, d/dx. Таким образом, если имеется функция y=f(x), то ее производная будет обозначаться как f'(x) или dy/dx.

Производная используется для решения широкого спектра математических задач, таких как определение точек экстремума функций, нахождение касательных и нормалей к кривым, анализ функций и т.д. Она также имеет широкое применение в науках, связанных с физикой, химией, экономикой, биологией и других дисциплинах.

Производительность в математике

Производительность в математике – это показатель эффективности работы над математическими задачами. Она определяется как количество задач, решенных за единицу времени. Для многих математиков производительность – это ключевой показатель, который характеризует их успехи и способности.

В математике производительность является важной как для учебных, так и для научных целей. Чем выше производительность математика, тем выше вероятность успеха в решении сложных математических проблем и тем больше научных статей и публикаций.

Одним из наиболее распространенных обозначений производительности в математике является скорость выполнения задач, измеряемая в числе задач, решенных за минуту. Например, если математик около 40 задач решил за 60 минут, то его производительность составляет 40/60=0,67 задач в минуту.

Другим показателем производительности в математике может быть точность выполнения задач, измеряемая в процентах решенных задач. Например, если математик решил 90% задач за 60 минут, то его производительность составляет 90%.

• Важность производительности в научных и учебных задачах.
• Обозначения производительности в математике: скорость и точность.

Видео по теме:

Что такое производительность и как ее измеряют?

Производительность — это показатель эффективности работы человека или машины в достижении конкретных результатов в заданный временной период. В математике производительность может выражаться в количестве выполненных действий, например, операций сложения, вычитания, умножения, деления.

Измерение производительности в математике может производиться с помощью простой формулы: количество выполненных действий, разделенное на время, затраченное на их выполнение. Например, если студент решил 50 математических задач за 1 час, то его производительность равна 50/1=50.

Однако, при измерении производительности в математике необходимо учитывать не только количество выполненных действий, но и их точность и сложность. Производительность, которая достигается за счет ошибок или плохого качества решений, не может считаться эффективной.

Также, для измерения производительности в математике можно использовать тесты с определенной сложностью и временными ограничениями. Это поможет определить уровень математических навыков и скорость их применения.

Знание показателей производительности может помочь улучшить математические навыки за счет увеличения скорости и точности выполнения действий.

Какие методы ускорения вычислений используются в математике?

В математике широко используются различные методы ускорения вычислений, которые позволяют решать задачи гораздо быстрее и эффективнее. Одним из таких методов является метод Монте-Карло. Он основан на использовании случайных чисел для симуляции процессов, таких как расчёт интеграла или нахождение площади фигуры.

Ещё один метод – метод Брента, который используется для нахождения корней функций. Он является итеративным методом и опирается на сочетание методов дихотомии и интерполяции. Это позволяет достигать высокой точности и скорости при нахождении корней.

В математике также широко применяются методы решения обыкновенных дифференциальных уравнений, такие как метод Эйлера и метод Рунге-Кутты. Они используются для моделирования различных процессов и программирования вычислительных алгоритмов.

Кроме того, очень эффективными методами в математике являются методы оптимизации, такие как метод градиентного спуска и методы линейного и квадратичного программирования. Они позволяют находить оптимальные решения задач в различных областях математики: от статистики и теории вероятности до оптимизации и управления системами.

1. Метод Монте-Карло – используется для симуляции процессов;
2. Метод Брента – используется для нахождения корней функций;
3. Методы решения обыкновенных дифференциальных уравнений – используются для моделирования различных процессов;
4. Методы оптимизации – используются для нахождения оптимальных решений в различных областях математики.

Что такое алгоритмическая сложность и как ее определить?

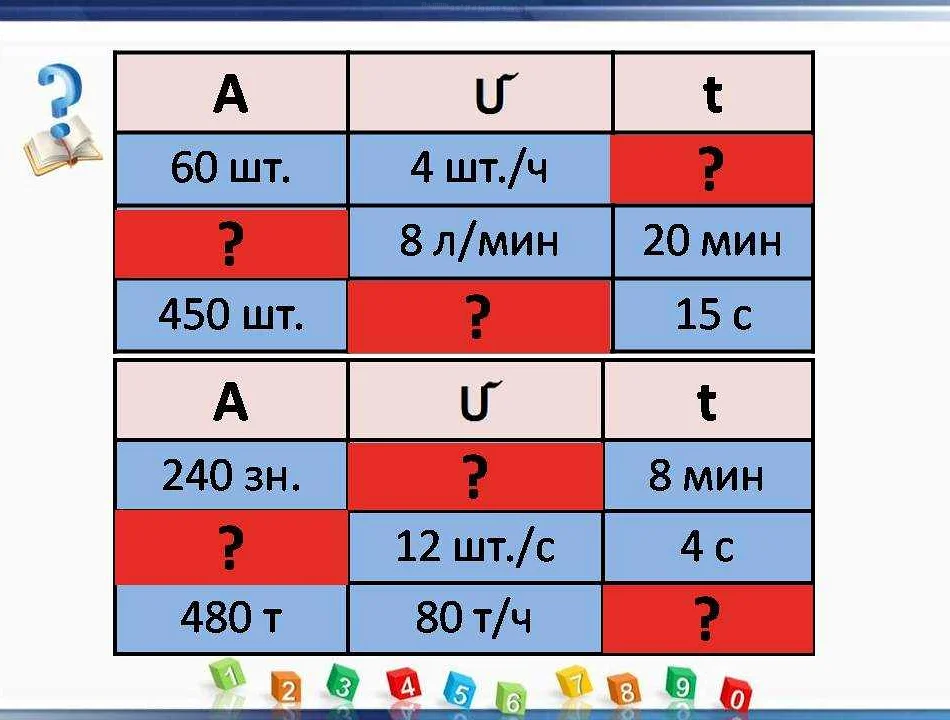
Алгоритмическая сложность — это понятие, которое описывает количество ресурсов, необходимых для выполнения конкретного алгоритма. Ресурсы могут быть различными: время, память, процессорные мощности и т.д.

Чтобы определить алгоритмическую сложность, необходимо оценить количество операций, которые должен выполнить алгоритм при обработке данных. Например, если алгоритм состоит из n шагов, и каждый шаг занимает постоянное количество времени, то общая сложность будет равна O(n).

Существуют разные типы алгоритмической сложности. Одним из таких типов является трудоемкость, которая может быть измерена в количестве операций или во времени выполнения алгоритма.

Для определения алгоритмической сложности могут использоваться различные методы, например, методы математического анализа, методы анализа данных и т.д.

Важно знать алгоритмическую сложность при разработке программных продуктов, так как от нее зависит скорость работы программы и ее эффективность. В свою очередь, это может влиять на удовлетворенность пользователями продуктом и его конкурентоспособность.

Какие методы оптимизации алгоритмов существуют?

Оптимизация алгоритмов — важный процесс, направленный на повышение производительности программного кода. Существует несколько методов оптимизации алгоритмов, которые можно применять:

• Использование эффективных алгоритмов: эффективный алгоритм — это алгоритм, который выполняет задачу за минимальное количество операций. Использование эффективных алгоритмов позволяет ускорить выполнение программного кода.
• Уменьшение сложности алгоритмов: сложность алгоритма зависит от количества операций, необходимых для его выполнения. Уменьшение сложности алгоритма позволяет сократить время выполнения программного кода.
• Кэширование: кэширование — это сохранение результата выполнения операции для последующего использования без повторного выполнения операции. Кэширование позволяет сократить время выполнения программного кода.
• Использование многопоточности: многопоточность — это параллельное выполнение нескольких задач. Использование многопоточности позволяет ускорить выполнение программного кода.

Каждый метод оптимизации алгоритмов имеет свои особенности и применяется в зависимости от конкретной ситуации. При оптимизации алгоритмов необходимо учитывать специфику задачи и выбирать наиболее подходящий метод оптимизации.

Что такое асимптотическая нотация?

Асимптотическая нотация — это математический инструмент, позволяющий описывать скорость роста функций приближенно. Эта нотация используется в анализе алгоритмов, теории сложности вычислений и других областях математики.

Для описания скорости роста функций в асимптотической нотации используются три символа:

• O(большая «о») – описывает ограничение сверху, то есть верхнюю границу роста функции;
• Ω(большая «омега») – описывает ограничение снизу, то есть нижнюю границу роста функции;
• Θ(большая «тета») – описывает точную скорость роста функции, когда она растёт не быстрее и не медленнее определенной функции.

Например, если функция f(n) растет не быстрее, чем g(n), то её можно записать как f(n) = O(g(n)).

Асимптотическая нотация позволяет выбирать наиболее эффективный алгоритм для решения задачи. Можно выбирать алгоритм, который имеет наименьшую асимптотическую сложность, то есть тот, который растет медленнее всех остальных алгоритмов при увеличении входных данных.

Также асимптотическая нотация позволяет сравнивать различные алгоритмы и определять их эффективность в обработке больших объёмов данных.

Какие виды асимптотической нотации применяются в математике?

Асимптотическая нотация — это способ описания поведения функции при стремлении аргумента к бесконечности. В математике применяются три основных вида асимптотической нотации: O-нотация, омега-нотация и тета-нотация.

O-нотация используется для описания верхней границы роста функции. Если функция f(x) имеет ограничение сверху по модулю константой g(x), говорят, что f(x) равна O(g(x)). O-нотация позволяет оценить временную сложность алгоритма. Например, алгоритм, выполняющийся за O(n^2), будет работать за время, пропорциональное квадрату размерности ввода.

Омега-нотация используется для описания нижней границы роста функции. Если функция f(x) имеет ограничение снизу по модулю константой g(x), говорят, что f(x) равна Ω(g(x)). Омега-нотация позволяет оценить наихудшее время выполнения алгоритма.

Тета-нотация используется для описания точной скорости роста функции. Если функция f(x) одновременно является O(g(x)) и Ω(g(x)), говорят, что f(x) равна θ(g(x)).

Применение асимптотической нотации очень важно в анализе алгоритмов и оптимизации программного обеспечения. Правильный выбор нотации позволяет оценить производительность системы и выбрать оптимальное решение.

Каким обозначением обозначается производительность алгоритмов в математике?

В математике для оценки производительности алгоритмов используется понятие «асимптотическая сложность».

Асимптотическая сложность описывает, как быстро растет время выполнения алгоритма с увеличением размера входных данных.

Обозначается асимптотическая сложность символом «O» и записывается как «O(f(n))», где «f(n)» — функция, описывающая скорость роста времени выполнения алгоритма в зависимости от размера входных данных.

Например, если время выполнения алгоритма растет линейно с размером входных данных, то его асимптотическая сложность будет описываться как «O(n)», где «n» — размер входных данных.

Знание асимптотической сложности помогает выбирать наиболее эффективные алгоритмы для решения задач и оптимизировать существующие алгоритмы.

Как понимать обозначение O(n) в контексте производительности алгоритмов?

Обозначение O(n) — это математическая нотация, используемая для описания производительности алгоритмов. Она позволяет оценить время выполнения алгоритма в зависимости от размера входных данных.

В обозначении O(n) буква «n» обозначает размер входных данных. Если алгоритм имеет оценку производительности O(n), то время его выполнения будет линейно зависеть от размера входных данных. Другими словами, при увеличении размера входных данных в k раз, время выполнения алгоритма также увеличится в k раз.

Например, если алгоритм с оценкой O(n) выполняется за 1 секунду для входных данных размером 100 элементов, то для входных данных размером 200 элементов он выполнится за 2 секунды, а для входных данных размером 300 элементов — за 3 секунды.

Обозначение O(n) является одной из самых распространенных оценок производительности алгоритмов. Однако, существуют и другие оценки, такие как O(log n), O(n^2), O(n log n) и т.д. Каждая из них характеризует, как быстро время выполнения алгоритма растет с ростом размера входных данных.

Важно понимать, что обозначение O(n) говорит о теоретической производительности алгоритма. При реальном выполнении может возникнуть множество факторов, влияющих на время его выполнения, таких как архитектура компьютера, оптимизация кода и т.д.

Как связана производительность алгоритмов с вычислительной сложностью задач?

Производительность алгоритмов и вычислительная сложность задач тесно связаны между собой. Любое решение задачи может быть реализовано различными алгоритмами, и их производительность может значительно отличаться друг от друга.

Вычислительная сложность задачи определяется временем выполнения алгоритма на определенном объеме данных. Чем больше объем данных, тем больше времени займет на алгоритм его выполнение. Следовательно, вычислительная сложность задачи обратно пропорциональна производительности алгоритма.

Чаще всего вычислительная сложность задачи описывается асимптотической сложностью в худшем/среднем случае. Это означает, что оценка сложности находится в пределах от нижней до верхней границы, которые зависят от размера входных данных. Асимптотическая сложность обозначается символом «O», который применяется для оценки функции роста времени выполнения алгоритма.

Таким образом, при разработке алгоритмов необходимо учитывать не только корректность, но и их производительность. Чтобы достичь лучших результатов, разработчикам необходимо использовать подходы, которые позволят сократить время выполнения алгоритма.

Какие примеры задач можно решить с помощью высокопроизводительных алгоритмов?

Высокопроизводительные алгоритмы могут быть использованы для решения множества задач в различных областях. Ниже представлены некоторые из них:

• Обработка больших объемов данных: высокопроизводительные алгоритмы позволяют обрабатывать и анализировать огромные объемы данных, которые практически невозможно обработать вручную.
• Искусственный интеллект: при обучении моделей искусственного интеллекта, необходимо обрабатывать большие объемы данных и вычислять множество математических операций. В этом случае высокопроизводительные алгоритмы помогают существенно ускорить процесс.
• Моделирование и оптимизация: при решении сложных задач, связанных с моделированием и оптимизацией, необходимо проводить множество вычислений. Высокопроизводительные алгоритмы позволяют справиться с такими задачами.
• Криптография: при создании различных систем безопасности используются сложные математические алгоритмы, которые можно решить только с помощью высокопроизводительных алгоритмов.

Высокопроизводительные алгоритмы являются важной составляющей в решении сложных задач, связанных с обработкой данных и математическим моделированием. Благодаря им, можно ускорить процесс вычислений и получить точные результаты в кротчайшие сроки.

Какая роль производительности в современной науке и технологиях?

Производительность – один из ключевых факторов, определяющих эффективность работы в различных областях науки и технологий. Она является главным критерием при выборе технологических решений и инструментов для работы с большими объемами данных.

В настоящее время важность производительности особенно заметна в сферах, связанных с искусственным интеллектом, большими данными, вычислительной техникой и многих других областях. Необходимость обработки и анализа огромных объемов информации требует высокой производительности системы, иначе результаты работы могут быть не только неточными, но и неполными.

Важно отметить, что производительность не сводится только к мощности вычислительной техники. Она включает в себя множество аспектов, в том числе оптимизацию алгоритмов и программного обеспечения, управление памятью, масштабируемость и многое другое. То есть производительность – это системный подход, предполагающий взаимодействие основных компонентов системы.

Таким образом, можно с уверенностью сказать, что производительность играет важную роль в разных областях науки и технологий. Она позволяет ускорить процессы обработки и анализа информации, повысить точность результатов, и, что немаловажно, сократить время на разработку и тестирование новых продуктов. В современном мире, где технологии развиваются с невероятной скоростью, производительность является одним из ключевых факторов в успехе любого проекта.

Вопрос-ответ:

Какое обозначение используется для производительности в математике?

В математике для обозначения производительности существует множество обозначений, но наиболее часто используемыми являются символ «P» и символ «T».

Что означает символ «P» для производительности в математике?

Символ «P» используется для обозначения производительности в математике и означает количество операций, которые может выполнить устройство за единицу времени. Например, P = 100M операций/сек.

Как измерить производительность в математике?

Производительность в математике измеряется различными способами, в зависимости от того, что именно требуется измерить. Например, можно измерять количество операций в секунду, скорость передачи данных или время выполнения определённых задач.

Как повлиять на производительность математических операций?

На производительность математических операций может повлиять множество факторов, таких как характеристики компьютера, оптимизация алгоритмов, объем данных и прочее. Для улучшения производительности можно использовать более мощное оборудование, оптимизировать алгоритмы, использовать параллельные вычисления и т.д.

Что такое производительность в обработке данных?

Производительность в обработке данных означает возможность обрабатывать большие объемы данных за определенный период времени. Чем выше производительность, тем быстрее устройство может обрабатывать данные и выполнять задачи.

Каким образом можно повысить производительность математических расчетов на компьютере?

Для повышения производительности математических расчетов на компьютере можно использовать оптимизацию алгоритмов и структур данных, использовать более мощное оборудование, увеличить объем оперативной памяти, использовать параллельные вычисления и т.д.

Как измерить скорость обработки процессором сложных функций в математике?

Скорость обработки процессором сложных функций в математике может измеряться при помощи бенчмарков, которые представляют собой тестовые задания, выполняющие определенные математические операции и измеряющие скорость их выполнения. Кроме того, можно также использовать профилирование кода с помощью специальных инструментов.