Что такое производной в математике

Что такое производная в математике: определение, примеры и применение. Узнайте, как производная функции описывает ее скорость изменения и позволяет решать различные задачи в физике, экономике и других областях науки и техники.

Производная — одно из основных понятий математического анализа, широко применяемое в различных областях науки и техники. Она описывает скорость изменения функции в каждой точке и позволяет выявлять множество интересных свойств и закономерностей.

Математически, производная функции в точке равна пределу отношения приращения функции к приращению независимой переменной. Она обозначается символом f’ или dy/dx. Производная может быть положительной или отрицательной, показывая направление изменения функции.

Производная имеет фундаментальное значение в математике. Она позволяет находить экстремумы функций, определять исчезновение наклона, находить точки перегиба и многое другое. Производная является ключевым инструментом в решении задач оптимизации, моделирования и прогнозирования.

Рассчитать производную можно с помощью различных методов: дифференцирования по определению, правила дифференцирования, приближенных методов и т.д. Каждый метод имеет свои особенности и применим в определенных случаях.

Определение производной

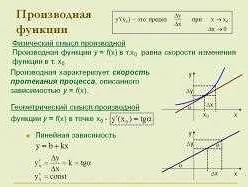
Производная обозначается символом f'(x) или dy/dx. Она может интерпретироваться как тангенс угла наклона касательной линии к графику функции в данной точке.

Производная функции показывает, как величина функции меняется при изменении ее аргумента. Если производная положительна, то функция возрастает, если отрицательна — функция убывает. Значение производной равное нулю указывает на экстремум функции.

Расчет производной может быть выполнен с использованием различных методов, таких как правило дифференцирования функций по формулам или дифференцирование исходной функции по правилам дифференцирования. Однако, в общем случае, производная может быть рассчитана путем нахождения предела разности значений функции в бесконечно близких точках.

Понимание производной функции позволяет решать различные задачи, связанные с оптимизацией, анализом функций и физическими явлениями, где важно знать скорость изменения величины по отношению к другой величине.

Видео по теме:

Геометрическая интерпретация производной

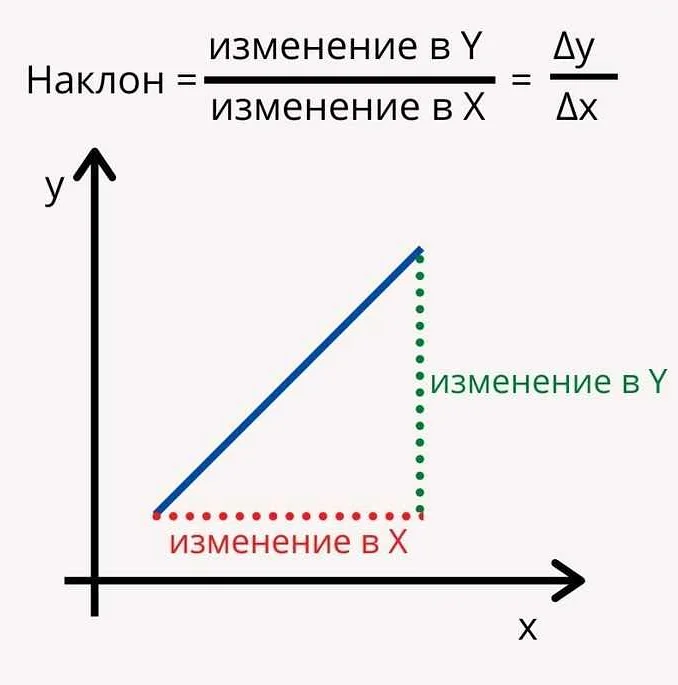
Производная функции в математике имеет не только алгебраическую, но также и геометрическую интерпретацию. Геометрически производная функции определяет угловой коэффициент касательной к графику функции в каждой точке.

Допустим, у нас есть функция f(x), график которой представлен на плоскости. Пусть x0 — точка на графике этой функции. Если производная f'(x0) существует в этой точке, то ее значение равно угловому коэффициенту касательной к графику функции в точке x0.

Таким образом, геометрически производная позволяет нам определить, как меняется функция в каждой точке графика: крутизну, наклон, направление.

Если значение производной положительное, то касательная к графику будет направлена вверх. Если значение производной отрицательное, то касательная будет направлена вниз. Если значение производной равно нулю, то касательная будет горизонтальной.

Геометрическая интерпретация производной позволяет нам лучше понять поведение функции и ее графика в различных точках. Она также является основой для решения геометрических задач, связанных с оптимизацией и поиском экстремумов функции.

Формулы для расчета производной

Существует несколько основных формул для расчета производной. Вот некоторые из них:

1. Формула мощности: f'(x) = nx^(n-1), где n — степень полинома.
2. Формула для суммы: f'(x) = g'(x) + h'(x), где g(x) и h(x) — функции.
3. Формула для разности: f'(x) = g'(x) — h'(x), где g(x) и h(x) — функции.
4. Формула для произведения: f'(x) = g(x) * h'(x) + g'(x) * h(x), где g(x) и h(x) — функции.
5. Формула для частного: f'(x) = (g'(x) * h(x) — g(x) * h'(x)) / (h(x))^2, где g(x) и h(x) — функции.
6. Формула для композиции: f'(x) = g'(h(x)) * h'(x), где g(x) и h(x) — функции.

Это лишь некоторые из основных формул для расчета производной. Существует много других формул, которые могут использоваться в зависимости от конкретной ситуации. Знание этих формул помогает упростить процесс расчета производной и ускорить его выполнение.

Вопрос-ответ:

Что такое производная и зачем она нужна?

Производная — это понятие из математического анализа, которое показывает, как изменяется функция в различных точках. Она позволяет определить скорость изменения функции в конкретной точке, а также позволяет находить экстремумы функций, т.е. точки максимума и минимума. Производная имеет широкое применение в физике, экономике, биологии и других науках, где есть необходимость в анализе изменения различных величин.

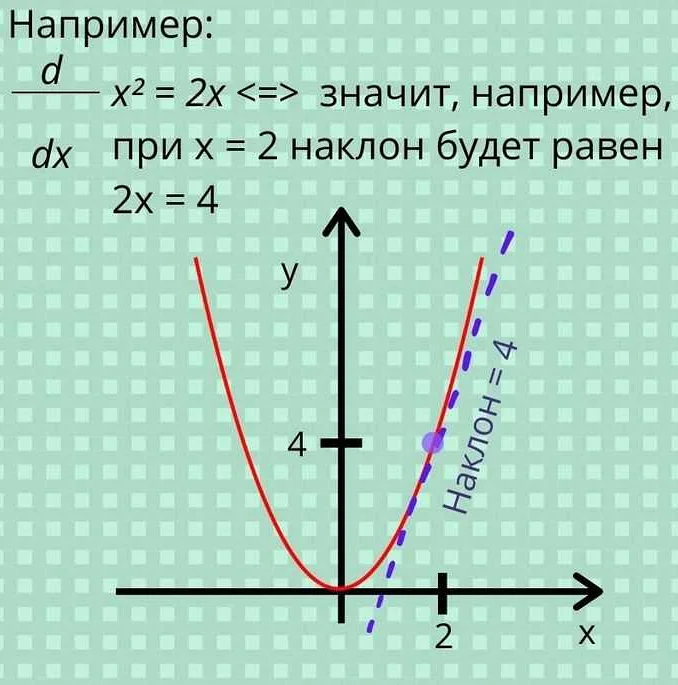
Как рассчитать производную функции?

Для того чтобы рассчитать производную функции, необходимо использовать определенные правила и формулы. Одно из основных правил — это правило дифференцирования степенной функции. Например, для функции y = x^2 производная будет равна 2x. Существуют также другие правила дифференцирования, такие как правило суммы, правило произведения, правило частного и т.д. В каждом конкретном случае необходимо использовать соответствующее правило и знать основные формулы для рассчета производной функции.

Какие применения имеет производная в реальной жизни?

Производная имеет широкое применение в различных областях науки и жизни. Например, в физике производная позволяет определить скорость изменения положения тела, ускорение, силу и другие физические величины. В экономике производная используется для определения эластичности спроса и предложения, максимизации прибыли и других экономических величин. В биологии производная применяется для определения скорости изменения популяции, роста организмов и других биологических процессов.

Какова связь между производной и графиком функции?

Связь между производной и графиком функции заключается в следующем: значение производной в конкретной точке графика функции показывает, каким образом меняется функция в этой точке. Если значение производной положительно, то функция возрастает в данной точке, если отрицательно — функция убывает. Ноль производной указывает на точку экстремума, т.е. максимума или минимума функции. Таким образом, график функции и ее производная взаимосвязаны и помогают понять ее поведение и свойства.

Что такое производная в математике?

Производная в математике — это понятие, которое описывает скорость изменения функции в каждой ее точке. Она позволяет понять, как функция меняется при изменении аргумента и найти угол наклона касательной к графику функции.

Как рассчитать производную?

Для того чтобы рассчитать производную функции, необходимо использовать определенные правила и формулы. Например, для нахождения производной элементарной функции нужно знать таблицу производных, а для нахождения производной сложной функции необходимо использовать правило цепочки или правило производной сложной функции.

Какая польза от производной в математике?

Производная является одним из основных инструментов математического анализа и находит множество применений в различных областях. Она помогает оптимизировать процессы, находить точки экстремума, анализировать траектории движения, моделировать и предсказывать изменения и многое другое. Производная также играет важную роль в физике, экономике, биологии и других науках.

Производная как скорость изменения

Интуитивно можно представить производную как скорость изменения значения функции в зависимости от изменения ее аргумента. Например, если функция описывает движение тела, то производная позволяет определить его скорость в каждый момент времени.

Формально, производная функции определяется как предел отношения изменения значения функции к изменению ее аргумента при бесконечно малом приращении аргумента. Производная обозначается символом f'(x) или df/dx.

Расчет производной можно выполнить аналитически, используя основные правила дифференцирования. Для этого необходимо знать алгебраическую формулу функции и применить соответствующие правила, такие как правило степенной функции, правило суммы, правило произведения и т.д.

Производная функции имеет важное значение во многих областях науки и техники. Она позволяет определить точки экстремума функции (максимумы и минимумы), а также анализировать графики функций и исследовать их поведение.

Применение производной в математике

Одним из основных применений производной является определение экстремумов функций. Производная позволяет найти точки, в которых функция достигает своих максимумов и минимумов. Это может быть полезно, например, при оптимизации процессов или решении задач на поиск наиболее эффективного решения.

Также производная позволяет анализировать поведение функции в различных точках. С помощью производной можно определить, является ли функция возрастающей или убывающей в определенном интервале. Это может быть полезно при изучении различных явлений в естественных и социальных науках.

Производная также позволяет решать задачи на нахождение скорости и ускорения. Например, в физике производная используется для определения скорости движения тела или изменения его положения во времени.

В экономике производная может быть использована для анализа спроса и предложения на рынке. Она позволяет определить, насколько изменение цены влияет на количество товара, которое покупают или продают.

Таким образом, производная является мощным инструментом анализа и решения различных задач в математике, физике, экономике и других науках.

Производная высших порядков

Для вычисления производной высших порядков необходимо последовательно применять операцию дифференцирования к функции. Например, производная второго порядка получается путем дифференцирования первой производной, производная третьего порядка — путем дифференцирования второй производной, и так далее.

При вычислении производной высших порядков важно учитывать порядок дифференцирования. Изменение порядка дифференцирования может привести к разным результатам. Например, производная второго порядка функции может быть отличной от производной первого порядка от первой производной.

Производные высших порядков широко используются в различных областях математики и физики для анализа и моделирования сложных явлений. Они позволяют более точно описывать изменения и свойства функций, а также находить точки экстремума, точки перегиба и другие характеристики функций.

Вычисление производных высших порядков может быть сложной задачей, особенно для сложных функций. Для этого используются различные методы и техники, такие как правила дифференцирования, формулы Лейбница, правило Лопиталя и др. В некоторых случаях может потребоваться использование компьютерных программ для численного вычисления производных.

Важно отметить, что производные высших порядков могут иметь различную интерпретацию в зависимости от контекста. Например, в физике производная второго порядка может описывать ускорение, а в экономике — эластичность спроса. Поэтому важно учитывать специфику задачи и выбирать соответствующую интерпретацию производной высших порядков.

Производная и графики

График функции является визуальным представлением ее поведения и зависимости от переменных. Производная функции позволяет анализировать ее график и выявлять особенности, такие как экстремумы, точки перегиба и т.д.

Из графика функции можно сделать несколько выводов о ее производной:

• Если график функции возрастает, то ее производная положительна.
• Если график функции убывает, то ее производная отрицательна.
• Если график функции имеет горизонтальную касательную, то ее производная равна нулю.
• Если график функции имеет вертикальную касательную, то ее производная не существует.

По графику функции можно определить, в каких точках у нее есть максимумы и минимумы. Для этого нужно найти точки, в которых производная меняет знак с положительного на отрицательный или наоборот.

Графическое представление функции и ее производной позволяет наглядно представить взаимосвязь между ними и делать выводы о поведении функции в разных точках.