Пропорционально в математике это как

Пропорциональность в математике — это отношение, при котором две величины меняются одновременно с одинаковым коэффициентом. Это позволяет предсказывать изменение одной величины на основе изменения другой и использовать пропорции для решения различных задач и проблем. Узнайте больше о том, как работает пропорциональность в математике и как ее применять.

Пропорциональность — одно из фундаментальных понятий в математике, которое позволяет описывать зависимость между двумя или более величинами. В математическом смысле, пропорциональность означает, что изменение одной величины приводит к соответствующему изменению другой, и это изменение происходит с постоянным коэффициентом пропорциональности.

Чтобы понять, как работает пропорциональность, можно рассмотреть простой пример: скорость движения автомобиля и время, затраченное на преодоление определенного расстояния. Если скорость увеличивается, то время, необходимое для преодоления расстояния, уменьшается. И наоборот, если скорость уменьшается, время увеличивается. В данном случае скорость и время пропорциональны друг другу.

Определение пропорциональности можно выразить следующей формулой: если a и b — две величины, то они пропорциональны, если их отношение a/b является постоянным значением, то есть не зависит от изменения a и b. Пропорциональность обычно обозначается символом ∝ (альфа).

Пропорциональность является важным понятием в математике и применяется в различных областях, включая физику, экономику, геометрию и даже искусство. Знание и понимание пропорциональности позволяет более точно анализировать и описывать взаимосвязи между величинами и делать более обоснованные выводы.

Что такое пропорционально в математике?

Пропорциональность можно представить в виде пропорции, которая выглядит следующим образом:

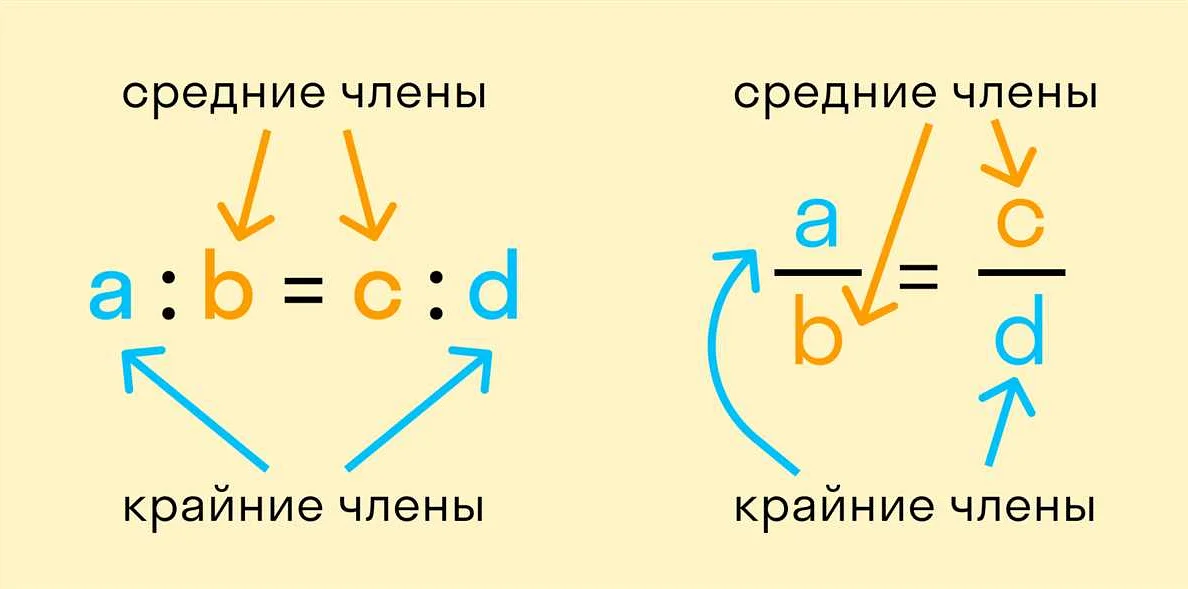
a : b = c : d

Здесь a и b представляют первый набор чисел или величин, а c и d – второй набор. Пропорциональность означает, что отношение между a и b равно отношению между c и d.

Пропорциональность можно представить и в виде уравнения:

a / b = c / d

Пропорциональные величины могут быть выражены как простые числа, физические величины, доли, проценты и т. д. Пропорциональность помогает нам понять и предсказать, как изменится одна величина при изменении другой. Например, если увеличить одну величину в два раза, то другая величина также увеличится в два раза, если они пропорциональны.

Пропорциональные отношения: определение и свойства

Определение пропорциональности можно представить следующим образом: если при изменении значений одного отношения значения другого отношения также изменяются в определенной пропорции, то эти отношения считаются пропорциональными.

Свойства пропорциональных отношений:

СвойствоОписание

Сохранение отношения	Если два отношения пропорциональны, то их значения обладают одинаковым отношением. Например, если отношение a:b равно отношению c:d, то оно будет равно отношению a:b = c:d = k, где k — постоянная пропорциональности.
Умножение и деление	Если отношение a:b пропорционально отношению c:d, то оно также будет пропорционально отношению ka:kb и отношению a/b:c/d. Также, если отношение a:b пропорционально отношению c:d, то оно будет пропорционально их обратным отношениям 1/a:1/b и 1/c:1/d.
Сложение и вычитание	Если отношение a:b пропорционально отношению c:d, а отношение c:d пропорционально отношению e:f, то отношение a:b также будет пропорционально отношению e:f. Также, если отношение a:b пропорционально отношению c:d, то отношение a+c:b+c будет пропорционально отношению c:d.

Пропорциональные отношения широко используются в различных областях, таких как физика, экономика, статистика и геометрия.

Пропорциональное равенство: основные правила

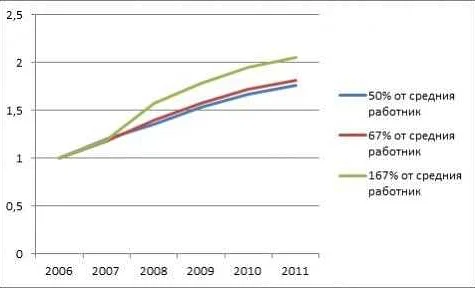
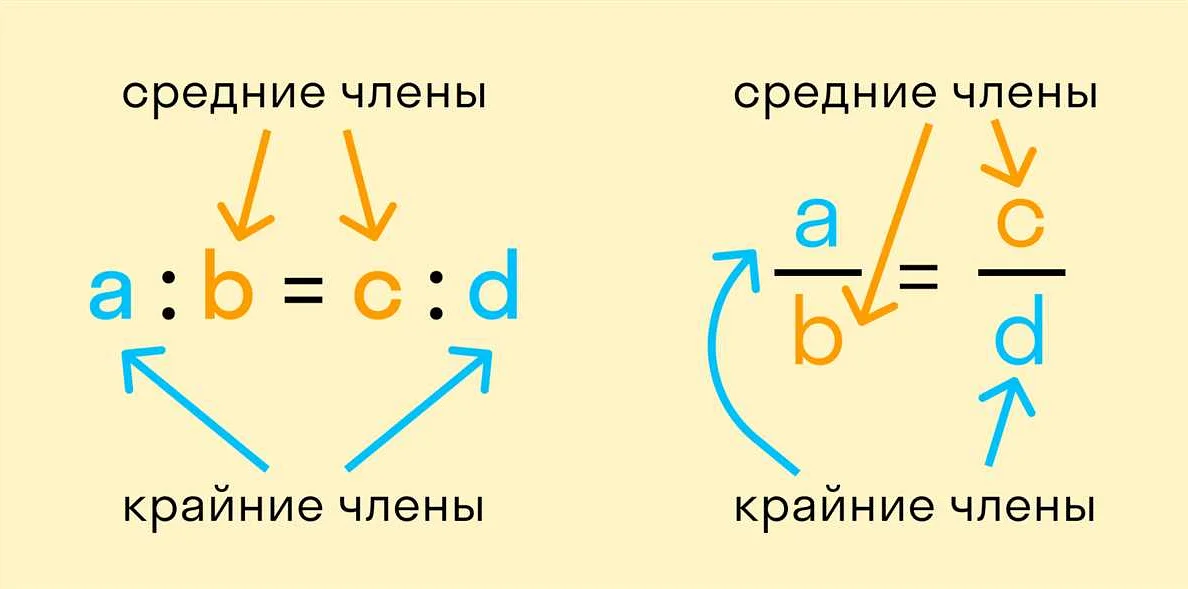
Основные правила пропорционального равенства:

1.	Если две пропорции равны, то их средние члены равны.
2.	Если две пропорции равны, то их крайние члены также равны.
3.	Если два отношения равны, то их средние члены пропорциональны.
4.	Если два отношения пропорциональны, то их произведения равны.
5.	Если два отношения пропорциональны, то их отношения равны.

Пропорциональное равенство применяется в различных областях математики и науки, а также в повседневной жизни, например, для расчета пропорций в рецептах или при решении финансовых задач.

Как найти пропорциональное число?

Для того чтобы найти пропорциональное число, нужно составить пропорцию с известными и неизвестными числами. Затем, применив правило трех, можно найти неизвестное число.

Правило трех гласит, что если в пропорции два отношения равны, то их произведения также равны. Для простоты можно записать правило трех следующим образом:

Известное число 1 / Известное число 2 = Неизвестное число 1 / Неизвестное число 2

Применяя правило трех к пропорции, можно найти неизвестное число. Для этого нужно умножить известное число 2 на неизвестное число 1 и разделить полученное произведение на известное число 1.

Например, если в пропорции известные числа равны 3 и 5, а неизвестные числа обозначены x и y, пропорция будет выглядеть следующим образом:

3 / 5 = x / y

Используя правило трех, можно найти значение x, умножив 5 на x и разделив полученное произведение на 3.

Пропорциональность в реальной жизни: примеры

1. Скорость и время: Если мы движемся с постоянной скоростью, то время, затраченное на преодоление определенного расстояния, будет пропорционально этому расстоянию. Например, если мы едем со скоростью 60 км/ч, то время, которое мы потратим на проезд 120 км, будет в два раза больше, чем время, затраченное на проезд 60 км.

2. Объем и масса: Плотность вещества может быть выражена как отношение массы к объему. Если плотность вещества не меняется, то масса и объем также будут пропорциональны. Например, если мы имеем два кубика одного материала, то масса одного из них будет в два раза больше, чем масса другого, если их объемы отличаются в два раза.

3. Зарплата и часы работы: В большинстве случаев зарплата работника зависит от количества отработанных им часов. Если ставка оплаты за час работы остается постоянной, то зарплата и количество отработанных часов будут пропорциональными. Например, если работник зарабатывает 10 долларов в час, то если он отработал 5 часов, то его зарплата будет в два раза меньше, чем если он отработал 10 часов.

Это лишь некоторые примеры пропорциональности в реальной жизни. Важно помнить, что пропорциональность является универсальным понятием, которое помогает нам понять и решить различные задачи, основанные на взаимосвязи между величинами.

Пропорциональность в геометрии: примеры и задачи

Примером пропорциональности в геометрии может служить отношение длин двух отрезков. Если отношение длин двух отрезков всегда остается постоянным независимо от их конкретных значений, то говорят, что эти отрезки пропорциональны. Например, если AB/CD = 2/3, то это означает, что любые два отрезка, подобные AB и CD, будут иметь отношение длин 2/3.

Другим примером пропорциональности в геометрии является отношение площадей двух подобных фигур. Если отношение площадей двух подобных фигур всегда остается постоянным независимо от их размеров, то говорят, что эти фигуры пропорциональны. Например, если площадь фигуры ABCD в два раза больше площади фигуры EFGH, то это означает, что любые две подобные фигуры, подобные ABCD и EFGH, будут иметь отношение площадей 2:1.

Пропорциональность в геометрии находит применение в различных задачах, например, для нахождения неизвестных длин, площадей или объемов. Решение таких задач требует использования свойств пропорциональности и умения составлять и решать пропорции.

ЗадачаРешение

Найти неизвестную сторону треугольника, если известны отношения сторон	Пусть сторона АВ треугольника АВС неизвестна. Известно, что АВ/ВС = 2/3. По свойству пропорциональности, можно записать: АВ/ВС = 2/3. Путем перестановки частей и умножения крест на крест получим: АВ = (2/3) * ВС.
Найти площадь подобной фигуры, если известно отношение площадей	Пусть площадь фигуры ABCD равна 16 квадратных единиц, а площадь фигуры EFGH равна 4 квадратных единиц. Известно, что площадь фигуры ABCD в два раза больше площади фигуры EFGH. По свойству пропорциональности, можно записать: ABCD/EFGH = 2/1. Переставим части и получим: ABCD = (2/1) * EFGH. Заменяем известные значения и получаем ABCD = (2/1) * 4 = 8 квадратных единиц.

Вопрос-ответ:

Что такое пропорциональность в математике?

Пропорциональность — это отношение между двумя величинами, при котором изменение одной величины приводит к соответствующему изменению другой величины.

Как определить пропорциональность?

Для определения пропорциональности необходимо проверить, что отношение между двумя парами чисел остается постоянным.

Какие примеры пропорциональности можно привести?

Примеры пропорциональности включают отношение между длиной и шириной прямоугольника, скоростью и временем путешествия, ценой и количеством товара.

Какие свойства имеет пропорциональность?

Пропорциональность обладает несколькими свойствами: 1) если две величины пропорциональны, то их произведение также пропорционально; 2) если две величины пропорциональны, то их отношение будет постоянным.

Может ли величина быть пропорциональна самой себе?

Нет, величина не может быть пропорциональна самой себе. Пропорциональность предполагает существование двух различных величин, которые находятся в определенном отношении друг к другу.

Золотое сечение как пример пропорциональности

Золотое сечение возникает при разделении отрезка на две части таким образом, что отношение длины всего отрезка к большей его части равно отношению большей части к меньшей:

ОтношениеЗначение

Длина отрезка к большей части	φ
Большая часть к меньшей части	φ — 1

Золотое сечение имеет множество интересных свойств и применений в различных областях, включая искусство, архитектуру и музыку. Оно часто встречается в пропорциях, формах и паттернах, которые считаются эстетически приятными и гармоничными.

Пропорциональность золотого сечения также используется в некоторых математических задачах и моделях, например, в фибоначчиевой последовательности и спирали.

Видео по теме: