Что значит рациональные числа в математике

Рациональные числа в математике — это числа, которые могут быть представлены в виде дробей, где числитель и знаменатель являются целыми числами. Они охватывают все десятичные дроби и целые числа, и являются важным понятием в алгебре и арифметике. Узнайте, как определить рациональные числа и как они используются в реальном мире.

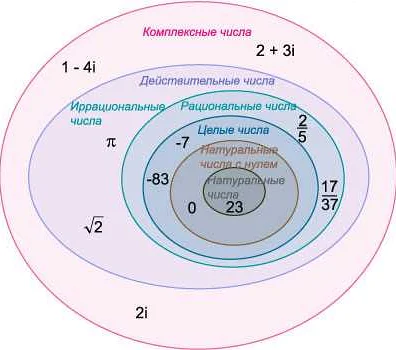
Рациональные числа — это особый класс чисел в математике, который включает в себя все числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами, а знаменатель не равен нулю. Понятие рациональных чисел является одним из фундаментальных понятий в математике и используется на протяжении всего курса обучения.

Рациональные числа отличаются от целых чисел тем, что они могут быть представлены в виде десятичных дробей, как конечных, так и бесконечных периодических. Например, число 1/2 является рациональным, так как оно может быть представлено в виде десятичной дроби 0.5. Также число 1/3 является рациональным, но оно будет представлено в виде бесконечной периодической десятичной дроби 0.33333…

Рациональные числа можно сравнивать, складывать, вычитать, умножать и делить. Они обладают свойством замкнутости относительно этих арифметических операций, то есть результатом любой арифметической операции с рациональными числами также является рациональное число.

Примеры рациональных чисел в математике могут быть как простыми, так и сложными. Например, число 2 является рациональным, так как оно может быть представлено в виде дроби 2/1. Также число -3/4 является рациональным, так как его можно представить в виде десятичной дроби -0.75.

Знание и понимание рациональных чисел является важным для понимания более сложных понятий в математике, таких как иррациональные числа и вещественные числа. Рациональные числа широко используются в реальной жизни, например, в финансовых расчетах, геометрии, физике и других областях науки и техники.

Рациональные числа в математике

Рациональные числа включают в себя все натуральные числа (1, 2, 3, …), все целые числа (…, -2, -1, 0, 1, 2, …), и все десятичные дроби (0.5, 0.333, 0.75, …). Они также включают числа, которые могут быть представлены конечными или повторяющимися десятичными дробями.

Рациональные числа могут быть отрицательными или положительными, их можно складывать, вычитать, умножать и делить друг на друга. Они играют важную роль в математике и имеют множество приложений в реальной жизни, таких как финансовые расчеты, измерения, геометрия и многое другое.

Примеры рациональных чисел:

• Целые числа: -3, 0, 1, 100
• Десятичные дроби: 0.5, 0.25, 0.333
• Обыкновенные дроби: 1/2, 3/4, 2/5

Рациональные числа являются одной из основных групп чисел в математике. Они обладают множеством свойств и правил, которые используются при решении различных задач и задач, связанных с числами.

Видео по теме:

Определение рациональных чисел

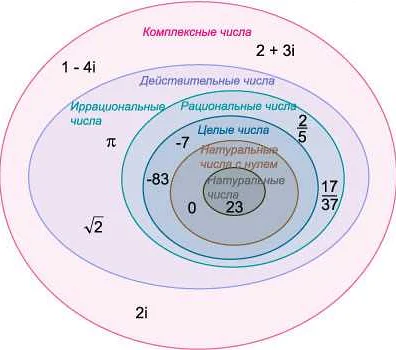
Рациональные числа включают в себя как целые числа (например, 0, 1, -1), так и десятичные дроби (например, 0.25, 1.5, -3.75). Числа могут быть как положительными, так и отрицательными.

Рациональные числа обладают следующими свойствами:

• Между любыми двумя рациональными числами существует еще одно рациональное число.
• Сумма, разность, произведение и отношение (кроме деления на ноль) двух рациональных чисел также являются рациональными числами.

Рациональные числа являются важной частью математики и широко используются в различных областях, включая физику, экономику и инженерию. Они помогают моделировать и анализировать реальные явления и являются основой для более сложных числовых систем.

Свойства рациональных чисел

Рациональные числа обладают рядом важных свойств, которые делают их полезными и удобными для работы в математике. Некоторые из этих свойств включают:

СвойствоОписание

Замкнутость относительно операций	Рациональные числа являются замкнутыми относительно основных арифметических операций — сложения, вычитания, умножения и деления. Это означает, что результат этих операций с рациональными числами всегда будет являться рациональным числом.
Свойства сложения и умножения	Рациональные числа обладают свойствами коммутативности, ассоциативности и дистрибутивности относительно сложения и умножения. Например, для любых рациональных чисел a, b и c справедливы равенства: a + b = b + a (коммутативность сложения), a + (b + c) = (a + b) + c (ассоциативность сложения), a * (b + c) = (a * b) + (a * c) (дистрибутивность умножения).
Свойство обратных элементов	Каждое рациональное число имеет обратное число, которое при умножении на него дает единицу. Например, для любого рационального числа a существует рациональное число b, такое что a * b = 1.
Свойство нуля	Рациональные числа также обладают свойством нуля, то есть для любого рационального числа a, a + 0 = 0 + a = a.

Эти свойства позволяют рациональным числам быть мощным инструментом для решения математических задач и применения в различных областях науки и техники. Понимание и использование этих свойств является важной частью изучения и работы с рациональными числами.

Примеры рациональных чисел

1. Целые числа: Целые числа, такие как 0, 1, -2, 3 и т.д., являются рациональными числами, так как их можно представить в виде дроби со знаменателем 1.

2. Десятичные дроби: Десятичные дроби, такие как 0,5, 0,333, 0,25 и т.д., также являются рациональными числами. Они могут быть представлены в виде дробей с целым числителем и степенью десяти в знаменателе.

3. Периодические десятичные дроби: Периодические десятичные дроби, например, 0,333… (0,3̅), 0,1666… (0,1̅6), также являются рациональными числами. Они могут быть представлены в виде дробей с числителем, равным периоду десятичной дроби, и знаменателем, равным числу девяток, соответствующему количеству цифр в периоде.

4. Смешанные числа: Смешанные числа, такие как 3 1/2, 2 3/4 и т.д., также являются рациональными числами. Они могут быть представлены в виде суммы целого числа и обыкновенной дроби.

Примеры рациональных чисел демонстрируют, что они могут быть представлены в различных формах и использоваться для описания различных ситуаций в математике и реальном мире.

Рациональные числа в десятичной форме

Когда рациональное число представляется в десятичной форме, оно может быть записано в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.

Конечная десятичная дробь представляется в виде десятичной запятой, за которой следует определенное количество цифр. Например, число 0,25 является конечной десятичной дробью, так как оно может быть записано в виде 1/4.

Бесконечная периодическая десятичная дробь состоит из бесконечного числа повторяющихся цифр, которые следуют после десятичной запятой. Например, число 0,333… представляет собой бесконечную периодическую десятичную дробь, которая может быть записана в виде 1/3.

Для представления рациональных чисел в десятичной форме можно использовать таблицу, где в каждой строке указаны числитель и знаменатель дроби, а в последнем столбце указано десятичное представление числа.

ЧислительЗнаменательДесятичное представление

1	2	0,5
1	4	0,25
1	3	0,333…

Таким образом, рациональные числа в десятичной форме могут быть представлены как конечные десятичные дроби, так и бесконечные периодические десятичные дроби.

Рациональные числа в виде дробей

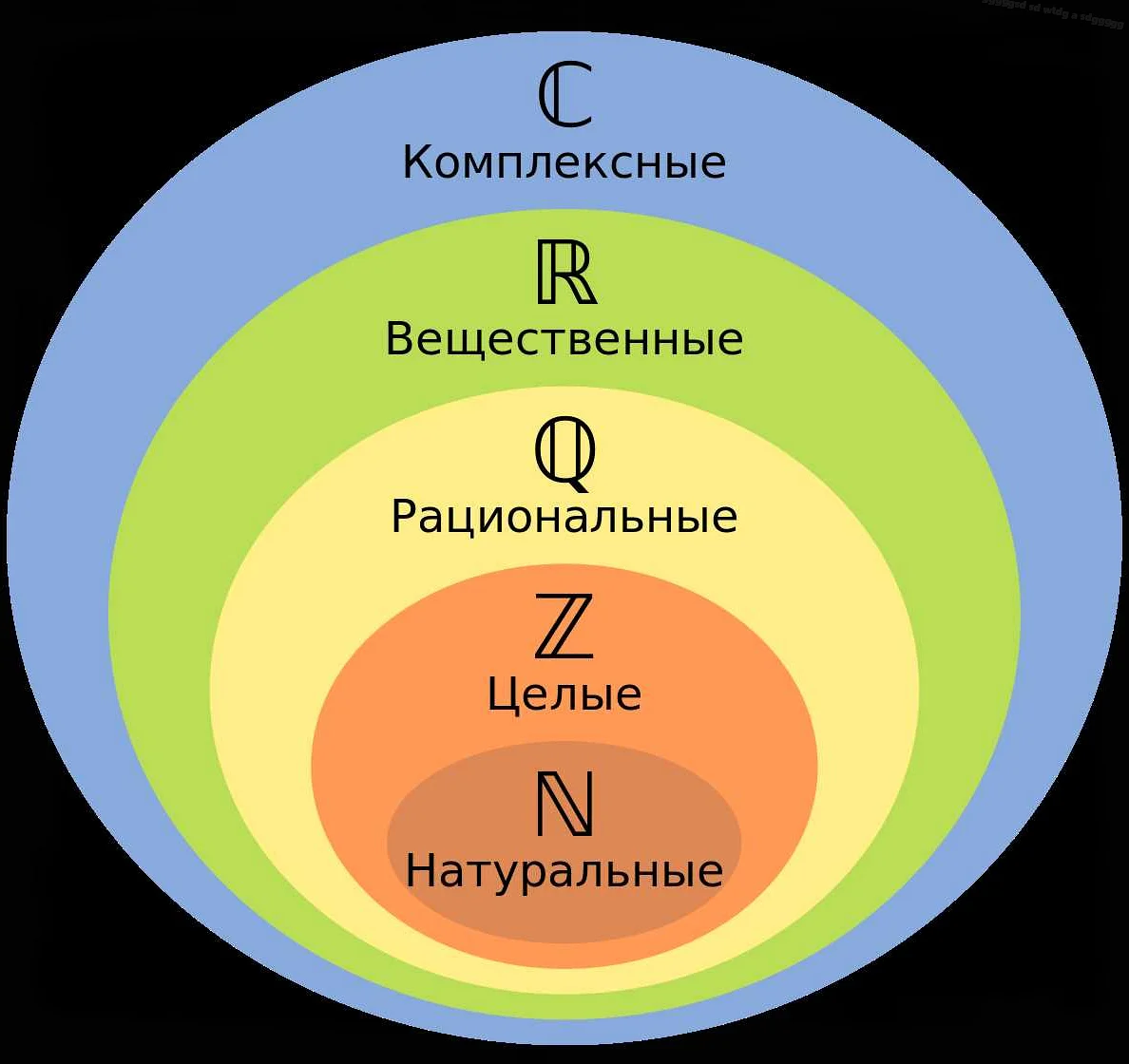
Например, число 3/4 является рациональным числом, так как его можно представить в виде дроби, где числитель равен 3, а знаменатель равен 4.

Рациональные числа можно складывать, вычитать, умножать и делить друг на друга, используя правила арифметики. Например, сумма двух рациональных чисел 1/2 и 1/3 равна 5/6.

Рациональные числа играют важную роль в математике и используются во многих областях, таких как физика, экономика и информатика. Они позволяют точно описывать и решать разнообразные задачи, связанные с долей и долевыми величинами.

Арифметические операции с рациональными числами

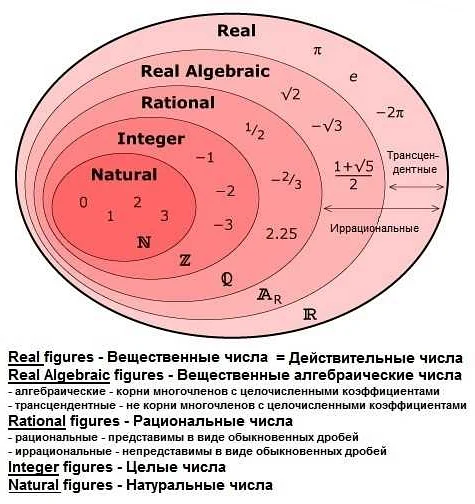
Сложение рациональных чисел происходит путем сложения числителей и знаменателей. Для этого необходимо найти общий знаменатель и привести дроби к общему знаменателю. Затем сложить числители и оставить общий знаменатель. Полученную дробь можно сократить, если это возможно.

Вычитание рациональных чисел осуществляется аналогично сложению. Необходимо найти общий знаменатель, привести дроби к общему знаменателю и вычесть числители.

Умножение рациональных чисел проводится путем умножения числителей и знаменателей. Полученную дробь также можно сократить.

Деление рациональных чисел происходит путем умножения числителя первой дроби на знаменатель второй и деления результата на произведение знаменателя первой дроби на числитель второй.

Арифметические операции с рациональными числами позволяют выполнять различные вычисления и решать задачи, связанные с долями и дробями. Они имеют широкое применение в реальной жизни и в различных областях науки.

Рациональные числа и бесконечность

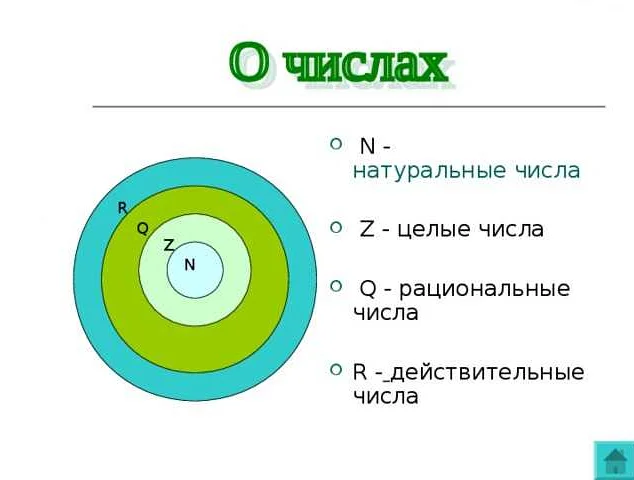
Рациональные числа могут быть бесконечными, когда знаменатель дроби равен нулю. Например, число 1/0 не имеет определенного значения, и его нельзя представить в виде конечной десятичной дроби. Вместо этого, оно считается «бесконечностью».

Еще один пример бесконечного рационального числа — десятичная дробь 0.3333… (цифра 3 повторяется бесконечно). Хотя эта десятичная дробь может быть записана в виде обыкновенной дроби 1/3, она все равно является бесконечной, так как повторяющаяся тройка никогда не заканчивается.

Бесконечность в рациональных числах может представлять некоторые проблемы при решении математических задач. Например, когда мы выполняем операции с бесконечными числами, результат может быть неоднозначным или недостаточно точным. Поэтому в математике существуют специальные правила и методы работы с бесконечностями.

В заключение, рациональные числа могут быть бесконечными, когда знаменатель дроби равен нулю или когда десятичная дробь повторяется бесконечно. Бесконечность в рациональных числах может создавать определенные сложности при выполнении математических операций, и поэтому требуется особое внимание и аккуратность при работе с ними.

Вопрос-ответ:

Что такое рациональные числа?

Рациональные числа — это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами, а знаменатель не равен нулю.

Какую роль играют рациональные числа в математике?

Рациональные числа являются важным понятием в математике, они позволяют представлять доли, долги, отношения и пропорции с точностью до бесконечности. Они используются во многих областях, включая физику, экономику, инженерное дело и другие науки.

Какие примеры рациональных чисел можно привести?

Примеры рациональных чисел включают такие числа, как 1/2, -3/4, 0, 2.5 и √9 (которое равно 3).

Как можно определить, является ли число рациональным?

Чтобы определить, является ли число рациональным, нужно проверить, может ли оно быть представлено в виде дроби, где числитель и знаменатель являются целыми числами. Если число может быть представлено в таком виде, то оно является рациональным.

Как связаны рациональные числа с целыми и натуральными числами?

Рациональные числа включают в себя целые и натуральные числа. Целые числа можно рассматривать как рациональные числа со знаменателем, равным 1. Натуральные числа можно представить в виде рациональных чисел со знаменателем, равным 1, и числителем, равным самому числу.