Что означает развернутая э в математике
Содержимое
- 1 Что означает развернутая э в математике
Развернутая форма э в математике представляет собой числовое выражение, включающее в себя комплексные и мнимые числа. Она используется для упрощения и решения сложных математических задач, а также для представления функций и уравнений. Умение работать с развернутой э позволяет математикам и инженерам успешно решать разнообразные проблемы в различных областях науки и техники.
Развернутая э, или математическая константа e, является одним из наиболее важных чисел в математике. Она была введена швейцарским математиком Леонардом Эйлером в середине XVIII века и с тех пор нашла широкое применение в различных областях науки и техники.
Определение развернутой э достаточно простое: e — это число, равное пределу (1 + 1/n)^n при n стремящемся к бесконечности. Приближенное значение развернутой э равно примерно 2.71828. Однако, в отличие от многих других чисел, развернутая э является иррациональным числом, то есть не может быть точно представлена в виде десятичной дроби или обыкновенной дроби.
Применение развернутой э в математике и естественных науках трудно переоценить. Она используется в анализе функций, дифференциальных уравнениях, теории вероятности и многих других областях. Развернутая э также играет ключевую роль в комплексном анализе и теории чисел. Более того, она неразрывно связана с логарифмическими, экспоненциальными и тригонометрическими функциями, что делает ее неотъемлемой частью математического аппарата.
В заключение можно сказать, что развернутая э является одним из фундаментальных и всеобъемлющих чисел в математике. Ее уникальные свойства и широкое применение делают ее необходимой для понимания и решения многих математических и научных задач.
Что такое развернутая э?
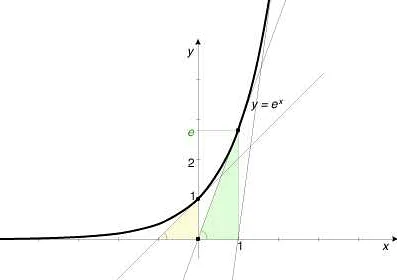
Основная особенность развернутой э заключается в том, что она является основанием экспоненциальной функции с основанием e. Экспоненциальная функция с основанием e имеет особые свойства и широкое применение в различных математических моделях.
Развернутая э также является ключевым элементом в формуле Эйлера, которая связывает три важных математических константы: развернутую э, комплексное число i и числа π. Формула Эйлера имеет вид eiπ+1=0 и считается одной из самых красивых формул в математике.
История развернутой э
Это число было введено швейцарским математиком Леонардом Эйлером в XVIII веке. Эйлер проводил исследования в области математического анализа и теории чисел, и ему было нужно найти показательную функцию, которая росла бы с постоянной скоростью.
Эйлер использовал бесконечный ряд, чтобы определить эту функцию. Ряд, который он использовал, называется рядом Тейлора и имеет вид:
e^x = 1 + x/1! + x^2/2! + x^3/3! + …
Этот ряд является бесконечным и растет с каждым новым слагаемым. Эйлер доказал, что сумма этого ряда равна развернутой э (e), и он стал первым математиком, который предложил использовать это число в математических вычислениях.
С течением времени развернутая э стала широко применяться в различных областях науки и техники. Она используется в физике, химии, экономике и других научных дисциплинах. Благодаря своим особенностям, развернутая э является незаменимым инструментом для решения различных задач и моделирования сложных процессов.
Символ развернутой э

Символ развернутой э широко используется в различных областях математики, включая теорию множеств, математическую логику, анализ и дискретную математику. Он позволяет указать, что определенный элемент принадлежит заданному множеству.
Например, если у нас есть множество натуральных чисел N = {1, 2, 3, …}, то можно записать «3 ∈ N», что означает, что число 3 принадлежит множеству натуральных чисел.
Также символ развернутой э может быть использован вместе с другими математическими символами, чтобы указать отношение между элементами множеств. Например, символ развернутой э может использоваться в комбинации с символом «не принадлежит» (∉) для обозначения отрицания принадлежности. Таким образом, если у нас есть множество целых чисел Z = {…, -2, -1, 0, 1, 2, …}, то можно записать «3 ∈ Z» для указания, что число 3 принадлежит множеству целых чисел, а «3 ∉ Z» для указания, что число 3 не принадлежит множеству целых чисел.
Применение развернутой э в математике
В теории вероятностей и математической статистике развернутая э используется для вычисления вероятностей и статистических характеристик случайных величин. В частности, она является основой для определения экспоненциального распределения, которое широко применяется при моделировании времени между событиями.
Развернутая э также является ключевым элементом в дифференциальном и интегральном исчислении. Она позволяет находить производные и интегралы функций с использованием правил дифференцирования и интегрирования. Это связано с тем, что производная и интеграл от функции ex имеют простую и удобную форму.
Кроме того, развернутая э используется в комплексном анализе и теории функций. Она позволяет определять и анализировать комплексные функции с помощью степенных рядов и дифференцирования. Важным применением развернутой э в этой области является формула Эйлера, которая устанавливает связь между различными математическими константами и комплексными функциями.
Наконец, развернутая э широко используется в физике и инженерных науках. Она встречается в уравнениях, описывающих различные физические явления, такие как распределение тепла, рост популяции, затухание сигнала и др. Также развернутая э играет важную роль в электротехнике и теории цепей, где она применяется при анализе и проектировании электрических цепей и систем.
Таким образом, развернутая э — неотъемлемый элемент математики, который находит применение во многих ее областях. Ее использование позволяет решать разнообразные задачи, связанные с вероятностью, анализом функций и моделированием физических явлений.
Применение развернутой э в физике

Развернутая э (экспоненциальная функция) широко применяется в физике для описания различных явлений и процессов. Ее особенности позволяют моделировать такие явления, как распределение электромагнитного поля, диффузия частиц, распад радиоактивных элементов и многое другое.
Одно из основных применений развернутой э в физике — описание процессов роста и распада. Например, закон радиоактивного распада основан на экспоненциальной функции, где скорость распада вещества пропорциональна количеству оставшихся нераспавшихся атомов. Это позволяет определить время полураспада и прогнозировать будущие значения количества вещества.
Еще одним применением развернутой э является описание изменения физических величин во времени. Например, при описании колебаний системы, величина колебаний может быть представлена экспоненциальной функцией, где амплитуда колебаний убывает или возрастает со временем в соответствии с определенным законом.
Также, развернутая э используется для описания распределения вероятности. В статистике и теории вероятности, различные законы распределения, такие как нормальное или пуассоновское распределение, могут быть описаны экспоненциальной функцией. Это позволяет анализировать различные случайные процессы и предсказывать вероятность их наступления.
Таким образом, развернутая э играет важную роль в физике, позволяя описывать и анализировать различные физические явления и процессы. Ее универсальность и широкое применение делают ее неотъемлемой частью физических исследований и моделирования.
Применение развернутой э в информатике
Одним из применений развернутой э в информатике является ее использование в алгоритмах и программировании. В некоторых алгоритмах эта символы используется для обозначения энергетических состояний или потенциала системы. Например, в алгоритмах оптимизации или симуляции развернутая э может быть использована для описания энергетических уровней и переходов между ними.
Развернутая э также может быть использована в информатике для обозначения электромагнитных полей или электромагнитного излучения. В различных алгоритмах моделирования физических процессов развернутая э может использоваться для описания электромагнитных явлений, таких как распространение света, электромагнитные волны и т.д.
Кроме того, развернутая э может быть использована в информационной безопасности. Например, в криптографии развернутая э может быть использована для обозначения степени шифрования или сложности системы защиты информации. Таким образом, символ развернутой э может быть включен в названия алгоритмов или протоколов, связанных с безопасностью информации.
Применение развернутой э в информатике
| Алгоритмы и программирование |
| Моделирование физических процессов |
| Информационная безопасность и криптография |
Применение развернутой э в других науках
- Физика: развернутая э используется для моделирования различных физических процессов, таких как распад атомных ядер, электромагнитные волны и изменение концентрации вещества во времени.
- Экономика: экспоненциальная функция широко используется для анализа экономических явлений, таких как рост населения, инфляция, экономический рост и инвестиции.
- Биология: экспоненциальный рост находит применение в моделировании популяционной динамики, эволюции организмов и распространения болезней.
- Компьютерные науки: экспоненциальные функции используются для оптимизации алгоритмов, анализа сложности задач и моделирования распределения данных.
Это лишь некоторые примеры применения развернутой э в других науках. В целом, экспоненциальные функции играют важную роль в моделировании и анализе различных процессов и явлений в разных областях знания.
Вопрос-ответ:
Что такое развернутая э в математике?
Развернутая э (или экспонента) в математике — это особая математическая функция, которая используется для выражения чисел в виде степени с основанием экспоненты, обычно обозначаемой как «е». Математически записывается как e^x, где x — это число, а e — это основание экспоненты, которое примерно равно 2,71828.
Какая особенность развернутой э в математике?
Особенностью развернутой э в математике является то, что она обладает свойством самоподобия. Это означает, что производная развернутой э равна самой развернутой э. Другими словами, производная функции e^x равна e^x. Это уникальное свойство делает развернутую э одной из наиболее важных и полезных функций в математике.
Какая практическая польза от использования развернутой э в математике?
Развернутая э имеет множество практических применений в различных областях науки и инженерии. Она используется для моделирования роста и распределения чисел, таких как популяция, инфляция, процентные ставки и другие экономические показатели. Развернутая э также используется в физике для описания процессов, связанных с теплопроводностью, распространением звука и электромагнитными волнами. Кроме того, развернутая э играет важную роль в теории вероятностей и статистике, а также в дифференциальных уравнениях и других разделах математики.
Как использовать развернутую э для решения математических задач?
Для использования развернутой э в решении математических задач необходимо знать ее основные свойства и формулы. Например, развернутая э обладает свойством коммутативности, то есть e^x * e^y = e^(x+y). Она также имеет свойство инверсии, то есть (e^x)^-1 = e^(-x). Эти свойства позволяют упрощать выражения с использованием развернутой э. Кроме того, развернутая э может быть использована для нахождения пределов функций, решения дифференциальных уравнений и других математических задач.
Что такое развернутая э в математике?
Развернутая э (или обратное е) — это математическое обозначение для числа, которое при умножении на число е равно единице. Она обычно обозначается как e^(-1) или exp(-1). Развернутая э является основой натурального логарифма и имеет множество приложений в математике и науке.
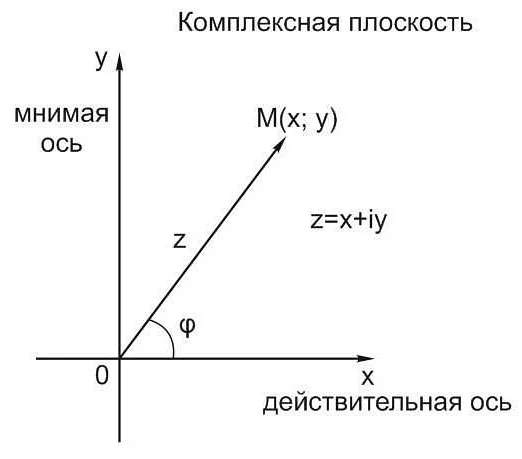


В статье очень хорошо и понятно объяснено, что такое развернутая э в математике. Видимо, это очень важное понятие, которое используется в различных областях науки и техники. Я, как обычный читатель, не особо знакомый с математикой, был приятно удивлен, как автор смог так просто и доступно объяснить это понятие. Теперь я понимаю, что развернутая э может быть использована для описания электрических полей, но и для других физических явлений. Статья дала мне интересные идеи, которые я, безусловно, буду исследовать дальше. Спасибо автору за такую информативную и понятную статью!
Прекрасная статья! Благодаря ей, я наконец-то поняла, что такое развернутая э в математике. Узнав о ее определении и применении, я почувствовала себя осведомленной в этой области. Как женщине, мне очень приятно видеть, что женские голоса и знания также присутствуют в математике. Этот символ играет важную роль в алгебре и теории чисел, что подтверждает его значимость. Теперь я чувствую себя увереннее в решении математических задач, где используется развернутая э. Большое спасибо за информативную и понятную статью! Я с нетерпением жду новых материалов от вас.
Отличная статья! Я всегда интересовался математикой и ее различными концепциями. Развернутая э — одна из таких интересных и полезных констант. Определение и применение развернутой э в математике действительно увлекательны. Важно понять, что это число представляет собой естественный логарифм от основания натуральных логарифмов. Это полезно при решении различных задач, таких как моделирование процессов роста и распада, анализ данных, решение уравнений и многое другое. Кроме того, развернутая э имеет ряд особенностей и свойств, которые делают ее незаменимой в математике. Она является иррациональным числом, что означает, что оно не может быть представлено в виде дроби. Это делает ее бесконечно точной и точно отражающей природу некоторых математических явлений. В заключение, развернутая э — фундаментальное число, которое широко используется в математике и имеет множество приложений. Ее определение и применение важно для понимания и использования различных математических концепций и методов. Статья дает хороший обзор этой темы и я надеюсь, что она будет полезна и другим читателям, интересующимся математикой.
Ваша статья очень интересна и полезна для всех, кто интересуется математикой. Я всегда была заинтригована одной буквой — э. Очень хорошо, что вы разъяснили ее значение и применение в математике. Благодаря вашим объяснениям, я лучше понимаю, как использовать эту букву в различных математических формулах и уравнениях. Это открывает новые возможности для меня и помогает мне глубже погрузиться в мир математики. Я также ценю вашу ясность и доступный стиль изложения. Ваши примеры и иллюстрации помогли мне лучше понять тему. Спасибо за эту информативную статью! Я определенно буду рекомендовать ее своим друзьям, которые также интересуются математикой.