Что такое троичная система счисления в математике
Содержимое
- 1 Что такое троичная система счисления в математике
- 1.1 Что такое троичная система счисления?
- 1.2 Видео по теме:
- 1.3 История развития троичной системы счисления
- 1.4 Особенности троичной системы счисления
- 1.5 Вопрос-ответ:
- 1.5.0.1 Какая основа у троичной системы счисления?
- 1.5.0.2 Как записываются числа в троичной системе счисления?
- 1.5.0.3 Как выполняются операции сложения и вычитания в троичной системе счисления?
- 1.5.0.4 В чем применение троичной системы счисления в математике?
- 1.5.0.5 Какие преимущества и недостатки имеет троичная система счисления по сравнению с десятичной?
- 1.5.0.6 Какая система счисления наиболее распространена в математике?
- 1.5.0.7 Чем отличается троичная система счисления от десятичной?
- 1.6 Основные принципы троичной системы счисления
- 1.7 Примеры использования троичной системы счисления
- 1.8 Применение троичной системы счисления в математике
- 1.9 Троичная арифметика
- 1.10 Кодирование информации с использованием троичной системы счисления
Троичная система счисления — это система, основанная на числе 3, в которой используются три символа для представления чисел. В этой системе счисления числа записываются с использованием цифр 0, 1 и 2. Троичная система счисления имеет свои особенности и применяется в различных областях, таких как компьютерные науки и криптография.
Система счисления – это метод представления чисел с помощью цифр. В нашей повседневной жизни мы привыкли использовать десятичную систему счисления, которая основана на использовании десяти цифр от 0 до 9. Однако, в математике существуют и другие системы счисления, включая троичную.
Троичная система счисления основана на использовании трех цифр: 0, 1 и 2. В такой системе каждая позиция имеет свой вес, который является степенью трех. Например, число 10 в троичной системе будет означать 1*3^1 + 0*3^0, что равно 3. Таким образом, троичная система счисления отличается от десятичной системы своим набором цифр и весом каждой позиции.
Особенностью троичной системы счисления является ее более компактное представление чисел. В десятичной системе для представления чисел требуется много цифр, а в троичной достаточно всего трех. Это делает троичную систему счисления особенно удобной в некоторых областях математики, где важна компактность представления данных.
Троичная система счисления также имеет свои применения в различных областях науки и техники. Она находит применение в криптографии, где используется троичный код для шифрования и дешифрования информации. Также, троичная система счисления используется в теории вероятностей и статистике, где она позволяет удобно работать с вероятностными распределениями и статистическими данными.
Троичная система счисления является одной из альтернативных систем счисления, которая отличается своим уникальным набором цифр и весом каждой позиции. Она имеет свои особенности и применение в математике, криптографии, теории вероятностей и статистике. Изучение троичной системы счисления позволяет получить глубокие знания о различных методах представления чисел и их применении в разных областях науки и техники.
Что такое троичная система счисления?
В троичной системе каждая позиция числа имеет вес, который равен степени тройки. Например, в числе 102 вес первой позиции равен тройке в степени 0, вес второй позиции равен тройке в степени 1, а вес третьей позиции равен тройке в степени 2. Это можно записать как 1 * 3^2 + 0 * 3^1 + 2 * 3^0.
Троичная система счисления используется в различных областях, включая математику, информатику, логику и электронику. В математике троичная система может применяться для решения различных задач, например, для представления чисел с большими разрядами или для выполнения операций с числами в троичном формате.
Троичная система счисления также может быть полезна в информатике и электронике, особенно при работе с технологиями, которые основаны на трех состояниях, например, триггеры или логические элементы с тремя входами. В таких случаях троичная система позволяет эффективно представлять и обрабатывать информацию.
Видео по теме:
История развития троичной системы счисления
Троичная система счисления, основанная на использовании трех цифр (0, 1 и 2), имеет древние корни. Первые упоминания о троичной системе счисления можно найти в древних культурах, таких как Мая, Инки и Эгейский мир.
Однако, наиболее подробные сведения о троичной системе счисления мы можем найти в работах арабских и индийских математиков, живших в IX-XIII веках. В Индии, например, троичная система счисления использовалась в некоторых областях математики и астрономии.
В Европе троичная система счисления начала активно развиваться в XVIII веке. Французский математик Готфрид Лейбниц активно работал над развитием этой системы. Он предлагал использовать троичную систему счисления в качестве основы для вычислений и логики. Однако, несмотря на эти попытки, троичная система счисления не получила широкого распространения и осталась в основном теоретической концепцией.
Сегодня троичная система счисления имеет свое применение в некоторых областях информатики, криптографии и математической логики. Она используется, например, в разработке троичных логических схем и квантовых вычислений. Кроме того, троичная система счисления может быть использована для представления данных, где требуется большая степень надежности и отказоустойчивости.
Особенности троичной системы счисления

В троичной системе счисления каждая позиция числа имеет вес, увеличивающийся втрое с каждой следующей позицией. Например, число 101 в троичной системе счисления представляет собой 1 * 3^2 + 0 * 3^1 + 1 * 3^0 = 1 * 9 + 0 * 3 + 1 * 1 = 10 в десятичной системе.
Одной из особенностей троичной системы счисления является возможность представления чисел без использования цифры 2. Вместо этого используются повторения цифр 0 и 1. Например, число 12 в троичной системе счисления представляется как 110 (1 * 3^2 + 1 * 3^1 + 0 * 3^0 = 1 * 9 + 1 * 3 + 0 * 1 = 12 в десятичной системе).
Троичная цифраДесятичное представление
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
Троичная система счисления имеет свои применения в математике, информатике и других областях. Она может быть использована для решения определенных задач, особенно в случаях, когда требуется компактное представление данных или высокая степень параллелизма. Кроме того, троичная система счисления может использоваться в некоторых формах музыкальной нотации и в криптографии.
Вопрос-ответ:
Какая основа у троичной системы счисления?
Основа троичной системы счисления равна 3.
Как записываются числа в троичной системе счисления?
В троичной системе счисления числа записываются с использованием трех цифр: 0, 1 и 2.
Как выполняются операции сложения и вычитания в троичной системе счисления?
В троичной системе счисления операции сложения и вычитания выполняются аналогично операциям в десятичной системе, но с использованием трех цифр.
В чем применение троичной системы счисления в математике?
Троичная система счисления применяется в математике для решения определенных задач, например, в криптографии, комбинаторике и теории вероятностей.
Какие преимущества и недостатки имеет троичная система счисления по сравнению с десятичной?
Преимущества троичной системы счисления включают возможность более компактного представления определенных числовых значений и более эффективного использования ресурсов компьютера. Однако, недостатком троичной системы счисления является большая сложность в понимании и использовании для обычных людей, привыкших к десятичной системе счисления.
Какая система счисления наиболее распространена в математике?
Наиболее распространена десятичная система счисления, которая использует десять цифр от 0 до 9.
Чем отличается троичная система счисления от десятичной?
Основное отличие троичной системы счисления от десятичной заключается в том, что в троичной системе используются только три цифры: 0, 1 и 2, в то время как в десятичной системе счисления используются десять цифр от 0 до 9.
Основные принципы троичной системы счисления
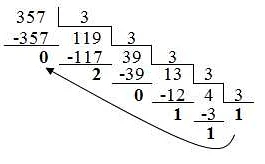
Троичная система счисления основывается на использовании трех цифр: 0, 1 и 2. Она отличается от десятичной системы, которая использует десять цифр от 0 до 9. В троичной системе каждая цифра имеет свое значение в зависимости от ее позиции в числе.
Основные принципы троичной системы счисления:
- Цифры в троичной системе: 0, 1 и 2. Они обозначают количество объектов или единиц каждой позиции числа.
- Позиционная система: значение каждой цифры зависит от ее позиции в числе. Чем правее цифра находится, тем больше ее вес.
- Умножение на основание: для перевода числа из троичной системы в десятичную необходимо умножить каждую цифру на основание системы в степени ее позиции.
- Сложение и вычитание: операции сложения и вычитания выполняются так же, как в десятичной системе, с учетом основания троичной системы.
- Применение в математике: троичная система счисления может быть использована для решения различных математических задач, таких как кодирование и декодирование данных, работа с троичными числами и операции над ними.
Троичная система счисления имеет свои преимущества и недостатки по сравнению с другими системами счисления. Она может быть полезной в определенных областях, где требуется работа с тернарными данными или оптимизация вычислений.
Примеры использования троичной системы счисления
Троичная система счисления имеет множество применений в математике и компьютерных науках. Рассмотрим несколько примеров использования данной системы:
1. Кодирование информации:
Троичная система счисления может использоваться для кодирования информации, особенно если она имеет три возможных состояния. Например, в сфере электроники и компьютерных наук троичные коды используются для представления состояний выключателей или ячеек памяти, которые могут быть в состоянии «0», «1» или «2». Такой подход позволяет сократить количество необходимых битов для хранения информации.
2. Решение задач комбинаторики:
Троичная система счисления может быть полезной при решении задач комбинаторики, таких как подсчет количества возможных комбинаций или перестановок. Например, при подсчете количества способов размещения трех различных предметов на трех различных местах, можно использовать троичную систему счисления, где каждая цифра представляет одну из трех позиций.
3. Численные методы:
Троичная система счисления может быть применена при использовании численных методов для решения задач, таких как численное интегрирование или решение дифференциальных уравнений. В некоторых случаях троичные числа могут обеспечить более точное представление численных данных и повысить точность вычислений.
4. Криптография:
Троичная система счисления может быть использована в криптографии для создания секретных ключей и шифрования информации. Троичные числа могут обеспечить более безопасное представление данных и усложнить процесс взлома.
Таким образом, троичная система счисления является мощным инструментом, который находит широкое применение в различных областях, где требуется более гибкое или эффективное представление чисел и информации.
Применение троичной системы счисления в математике
Троичная система счисления, основанная на использовании трех символов (0, 1 и 2), находит свое применение в различных областях математики. Вот несколько примеров:
- Кодирование и передача данных: троичная система счисления может использоваться для представления и передачи информации. Например, в компьютерных сетях троичные коды могут использоваться для эффективной передачи данных.
- Криптография: троичная система счисления может быть использована в некоторых криптографических алгоритмах для шифрования и дешифрования данных.
- Теория графов: троичная система счисления может быть применена для описания и анализа графов. Например, в задачах о раскрашивании графов троичные цвета могут быть использованы для обозначения различных вершин.
- Алгоритмы и вычисления: троичная система счисления может быть использована в некоторых алгоритмах и методах вычислений. Например, в алгоритме умножения чисел троичные цифры могут быть использованы для выполнения умножения в разрядах.
- Математические модели: троичная система счисления может быть использована для создания математических моделей и исследования различных явлений и процессов. Например, в моделировании поведения популяции троичные состояния могут быть использованы для описания различных состояний популяции (например, здоровья, болезни, смерти).
Таким образом, троичная система счисления имеет широкий спектр применения в математике и связанных областях. Ее использование позволяет эффективно представлять и обрабатывать информацию, решать сложные задачи и создавать математические модели.
Троичная арифметика
В троичной арифметике существует своя таблица сложения, которая определяет результат сложения двух троичных чисел. Например, при сложении 1 и 2 мы получим 10, а при сложении 2 и 2 – 11. Таким образом, в троичной арифметике для выполнения сложения можно использовать обычное правило сложения двух чисел, с учетом переноса из разряда в разряд.
Вычитание в троичной арифметике выполняется аналогично вычитанию в десятичной системе счисления. Если из одного троичного числа вычитается другое, то результат получается путем вычитания цифр в каждом разряде, с учетом переноса из более старших разрядов.
Умножение в троичной арифметике также осуществляется по аналогии с десятичной системой счисления. При умножении двух троичных чисел, каждая цифра первого числа умножается на каждую цифру второго числа, а затем полученные произведения складываются.
Деление в троичной арифметике также аналогично делению в десятичной системе счисления. При делении одного троичного числа на другое, производится последовательное вычитание, пока не будет достигнуто нулевое остаточное значение.
Троичная арифметика находит применение в различных областях, включая информатику, теорию кодирования и криптографию. Она используется, в частности, для кодирования и передачи информации, а также для выполнения арифметических операций в компьютерных системах.
Кодирование информации с использованием троичной системы счисления
Троичная система счисления, основанная на числе 3, может быть использована для кодирования информации. В отличие от двоичной системы счисления, которая использует только две цифры (0 и 1), троичная система позволяет представить числа в виде трех различных цифр: 0, 1 и 2.
Одним из применений троичной системы счисления является кодирование информации в компьютерных системах. В троичной системе можно представить каждый символ или букву, используя комбинацию трех цифр. Например, можно использовать цифры 0, 1 и 2 для кодирования букв алфавита или других символов.
В троичной системе счисления кодирование информации может происходить с использованием различных методов. Один из таких методов — непосредственное кодирование, при котором каждому символу или букве назначается определенная комбинация трех цифр. Другой метод — префиксное кодирование, при котором каждому символу или букве назначается определенный префиксный код, состоящий из комбинации цифр.
Кодирование информации с использованием троичной системы счисления позволяет увеличить количество возможных комбинаций символов или букв, что может быть полезно при передаче данных или хранении информации. Кроме того, троичная система счисления может быть использована в различных алгоритмах и математических задачах.



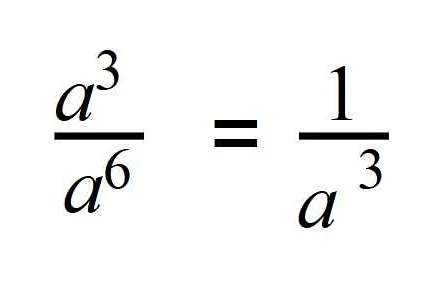
Статья очень интересная и познавательная! Я всегда задавался вопросом, почему мы используем десятичную систему счисления. И вот я узнаю, что есть троичная система счисления, основанная на числе 3. Это действительно удивительно! Я думаю, что использование троичной системы счисления может быть полезным в математике, особенно при работе с большими числами. К тому же, статья объясняет, что троичная система счисления может быть использована в компьютерных системах, таких как тригонометрия и кодирование. Я буду учитывать эту информацию и, возможно, попробую применить троичную систему счисления в своих математических расчетах. Спасибо за подробное объяснение и заинтересовавшую меня статью!