Сколько натуральных чисел в математике

Узнайте, сколько натуральных чисел существует в математике. Натуральные числа — это положительные целые числа, начиная с единицы. Узнайте, какие числа считаются натуральными и как их можно представить в математике. Познакомьтесь с особенностями натуральных чисел и их свойствами.

Натуральные числа – это числа, которые используются для подсчета предметов или выражения порядка. Они являются основной составляющей числовой системы и делятся на две категории: конечные и бесконечные. Конечные натуральные числа начинаются с единицы и увеличиваются на единицу по мере прибавления следующего числа. Бесконечные натуральные числа, с другой стороны, не имеют конечной границы и могут продолжаться до бесконечности.

Общее количество натуральных чисел трудно представить, так как они не имеют верхней границы. Каждое натуральное число можно считать последовательным шагом от предыдущего, и таким образом, количество натуральных чисел бесконечно. Математики используют символ бесконечности (∞) для обозначения этого понятия. Бесконечность натуральных чисел позволяет нам проводить бесконечные операции и создавать бесконечные последовательности.

Натуральные числа обладают несколькими свойствами, которые делают их особенными в математике. Во-первых, каждое натуральное число имеет преемника (следующее число), которое можно получить, увеличивая его на единицу. Во-вторых, каждое натуральное число, кроме единицы, имеет предшественника (предыдущее число), которое можно получить, уменьшая его на единицу. В-третьих, натуральные числа можно упорядочить в порядке возрастания или убывания, что позволяет нам сравнивать их и проводить операции сравнения.

Натуральные числа играют важную роль в математике и имеют множество приложений в реальном мире. Они используются во многих областях, таких как физика, экономика, информатика и многое другое. Понимание основных свойств натуральных чисел является фундаментальным для дальнейшего изучения математики и ее применения в практических задачах.

Сколько натуральных чисел в математике: общее количество и свойства

Свойства натуральных чисел включают:

1. Упорядоченность: натуральные числа можно упорядочить по возрастанию или убыванию.
2. Сложение и вычитание: натуральные числа можно складывать и вычитать друг из друга.
3. Умножение и деление: натуральные числа можно умножать и делить друг на друга.
4. Делители: каждое натуральное число имеет свои делители, которые являются другими натуральными числами, на которые это число делится без остатка.
5. Простые числа: натуральные числа, имеющие только два делителя — единицу и само число.
6. Составные числа: натуральные числа, имеющие больше двух делителей.

Натуральные числа играют важную роль в математике и используются во множестве различных задач и приложений. Они являются основой для изучения других групп чисел, таких как целые, рациональные и вещественные числа. Кроме того, они используются в различных областях науки и техники, включая физику, экономику и компьютерные науки.

Определение натуральных чисел

Натуральные числа образуют бесконечный набор чисел, которые можно записывать в десятичной системе счисления. Они имеют следующие свойства:

СвойствоОписание

Положительность	Натуральные числа всегда положительны и больше нуля.
Упорядоченность	Натуральные числа упорядочены по возрастанию, что означает, что каждое последующее число больше предыдущего.
Бесконечность	Натуральных чисел бесконечное множество, так как их количество неограничено.

Натуральные числа широко используются в математике и находят применение в различных областях науки и практики.

Сколько натуральных чисел существует

Натуральные числа удовлетворяют нескольким свойствам:

• Натуральные числа являются счетным множеством. Это означает, что можно упорядочить натуральные числа по возрастанию и пронумеровать их: первый, второй, третий и так далее.
• Натуральные числа не имеют конца. Независимо от того, насколько большое число мы возьмем, всегда можно найти число, которое будет больше.
• Натуральные числа образуют основу для других множеств чисел. Например, целые числа включают в себя натуральные числа плюс ноль и отрицательные числа.

Таким образом, количество натуральных чисел бесконечно и они играют важную роль в математике и ее приложениях.

Бесконечность множества натуральных чисел

Свойство бесконечности множества натуральных чисел можно формально описать следующим образом: если мы возьмем любое натуральное число, то всегда найдется следующее натуральное число, которое будет больше предыдущего.

Например, если мы возьмем число 5, то следующее натуральное число будет 6. Если мы возьмем число 100, то следующее натуральное число будет 101. Видно, что независимо от выбранного числа, всегда можно найти следующее число, которое будет больше предыдущего.

Бесконечность множества натуральных чисел является одним из фундаментальных свойств математики. Оно играет важную роль во многих областях, включая алгебру, анализ и теорию чисел.

Бесконечность множества натуральных чисел – это ключевое понятие, которое помогает нам понять и исследовать многие математические явления и закономерности.

Свойства натуральных чисел

Натуральные числа обладают рядом уникальных свойств:

Свойство	Описание
Порядок	Натуральные числа имеют определенный порядок: 1, 2, 3, и так далее. Любое натуральное число можно увеличить на единицу и получить следующее натуральное число.
Бесконечность	Множество натуральных чисел бесконечно. Нет наибольшего или наименьшего натурального числа.
Упорядоченность	Натуральные числа можно упорядочить по возрастанию или убыванию.
Арифметические операции	Над натуральными числами можно выполнять арифметические операции: сложение, вычитание, умножение, деление и возведение в степень.
Делители	Каждое натуральное число имеет делители, которые являются также натуральными числами.

Эти свойства позволяют нам работать с натуральными числами и использовать их в математических операциях и задачах.

Простые и составные числа

В математике натуральные числа можно разделить на две категории: простые и составные числа.

Простые числа — это числа, которые имеют только два делителя: 1 и само число. Примерами простых чисел являются 2, 3, 5, 7, 11, 13 и т.д. Простые числа не могут быть разложены на произведение других чисел.

Теорема о простых числах утверждает, что существует бесконечное количество простых чисел. Это значит, что всегда можно найти новое простое число, которое больше всех предыдущих.

Составные числа — это числа, которые имеют больше двух делителей. Они могут быть разложены на произведение простых чисел. Например, число 4 является составным, так как оно может быть разложено на произведение 2 * 2.

Классификация чисел на простые и составные является важной темой в теории чисел и имеет много практических применений, например, в криптографии и факторизации чисел.

Делимость и множители натуральных чисел

Для определения делимости двух чисел используется понятие «делитель». Число называется делителем другого числа, если оно делится на него без остатка. Например, число 6 делится на 2 без остатка, поэтому 2 является делителем числа 6. Если число делится на другое число без остатка, оно называется кратным этому числу. Например, число 10 кратно числу 5, так как оно делится на 5 без остатка.

Множители натурального числа представляют собой числа, на которые это число делится без остатка. Например, множители числа 12 являются числами 1, 2, 3, 4, 6 и 12, так как они все без остатка делят число 12. Множители могут быть положительными или отрицательными, но в случае натуральных чисел они всегда положительны.

Делимость и множители натуральных чисел играют важную роль в различных областях математики, таких как факторизация чисел, нахождение наименьшего общего кратного и наибольшего общего делителя, простота чисел и многое другое.

Связь натуральных чисел с другими множествами чисел

Существует связь натуральных чисел с другими множествами чисел, такими как целые, рациональные, действительные и комплексные числа.

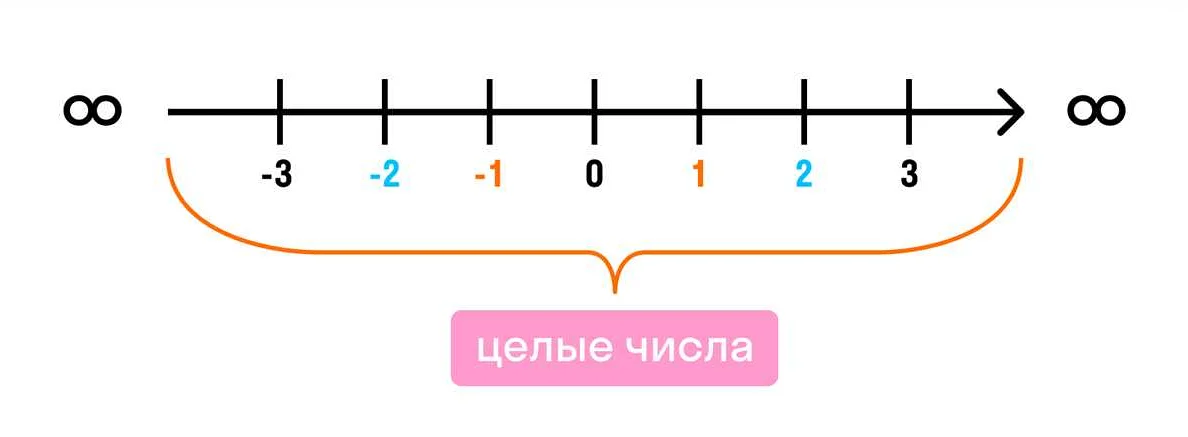
• Целые числа (обозначаются символом Z) включают в себя все натуральные числа, а также нуль и все отрицательные числа.
• Рациональные числа (обозначаются символом Q) включают все числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами.
• Действительные числа (обозначаются символом R) включают все числа на числовой прямой, включая рациональные числа и иррациональные числа, которые не могут быть представлены в виде дроби.
• Комплексные числа (обозначаются символом C) включают все числа, которые можно представить в виде a + bi, где a и b являются действительными числами, а i — мнимая единица.

Таким образом, натуральные числа являются одним из основных множеств чисел и являются частью более широких множеств чисел, таких как целые, рациональные, действительные и комплексные числа.

Практическое применение натуральных чисел

Натуральные числа играют важную роль в различных областях нашей жизни. Они используются для решения задач и описания количественных характеристик.

Одним из практических применений натуральных чисел является подсчет предметов или объектов. Например, при счете деталей на производстве или при оценке количества товаров на складе. Натуральные числа также используются для измерения времени, дат и возраста.

Натуральные числа играют значительную роль в математике и науке в целом. Они используются для построения математических моделей, решения уравнений и проведения различных исследований. Например, при моделировании распределения населения в городе или при анализе данных в экономике.

Кроме того, натуральные числа используются в информатике и программировании. Они используются для индексирования элементов в массивах, создания циклов и выполнения различных математических операций. Натуральные числа также широко применяются в алгоритмах и структурах данных.

В заключение, натуральные числа имеют множество практических применений в различных областях нашей жизни, начиная от счета предметов и измерения времени, и заканчивая математикой, наукой и информатикой. Они являются важным инструментом для описания и анализа количественных характеристик и решения различных задач.

Видео по теме:

Сколько всего натуральных чисел в математике?

В математике количество натуральных чисел бесконечно. Множество натуральных чисел обозначается символом N и состоит из чисел 1, 2, 3, 4, 5 и так далее до бесконечности.

Какие есть примеры натуральных чисел?

Примеры натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и так далее.

Какое множество чисел является бесконечным?

Множество натуральных чисел N является бесконечным, так как не имеет конечного верхнего предела.