Что такое смежные углы в математике

Смежные углы в математике — это пара углов, у которых вершина и одна сторона совпадают. Понимание понятия смежных углов важно для решения задач по геометрии и для понимания свойств угловых отношений. Узнайте больше о смежных углах и их применении в математике.

Смежные углы — это особый вид углов, которые имеют общую сторону и располагаются по одну и другую сторону этой стороны. Они часто встречаются в геометрии и играют важную роль в решении различных задач и построении фигур.

Основным свойством смежных углов является то, что их сумма равна 180 градусов. Это означает, что если мы знаем значение одного из смежных углов, мы можем найти значение другого угла, вычитая из 180 градусов известное значение. Это свойство позволяет использовать смежные углы для решения уравнений и нахождения неизвестных значений.

Например, если у нас есть два смежных угла, и мы знаем, что один угол равен 60 градусов, мы можем найти значение другого угла, вычитая 60 из 180. Таким образом, второй угол будет равен 120 градусам.

Смежные углы также могут быть вертикальными. Вертикальные смежные углы — это пары углов, которые образуются пересечением двух прямых линий. Они имеют общую вершину, но лежат по разные стороны от нее. Такие углы также имеют сумму, равную 180 градусов.

Изучение смежных углов помогает понять основные принципы и свойства геометрии, а также дает возможность применять их в практических задачах, связанных с архитектурой, инженерией и другими областями, где необходимо работать с геометрическими фигурами и их составляющими элементами.

Смежные углы: определение и основные свойства

При работе с смежными углами важно помнить следующие основные свойства:

1. Сумма смежных углов равна 180 градусам. Если у нас есть два смежных угла, то их сумма всегда будет равна 180 градусам.

2. Смежные углы образуют линейную пару. Линейная пара углов — это пара углов, которые лежат на одной прямой и в сумме дают 180 градусов. Смежные углы всегда являются линейной парой.

3. Смежные углы дополняют друг друга. Если у нас есть два смежных угла, то их сумма будет равна 180 градусам, следовательно, они будут дополнять друг друга.

4. Смежные углы могут быть как острыми, так и тупыми. Смежные углы могут находиться как по одну сторону от прямой, так и по противоположные стороны. Поэтому смежные углы могут быть как острыми, так и тупыми.

Знание определения и основных свойств смежных углов позволяет решать различные задачи в геометрии, а также применять их в повседневной жизни.

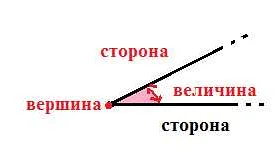
Смежные углы: геометрическое обозначение и измерение

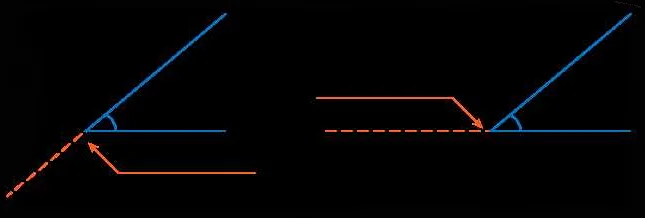
Измерение смежных углов производится с помощью градусной меры. Градус — это единица измерения угла, равная 1/360 полного оборота. Стандартное измерение угла обозначается числом, которое указывает количество градусов, на которое угол повернут относительно начальной стороны. Например, если угол повернут на 45 градусов, его измерение будет равно 45°.

Смежные углы могут быть как положительными, так и отрицательными. Положительные углы измеряются против часовой стрелки, а отрицательные — по часовой стрелке.

Важно отметить, что сумма измерений двух смежных углов всегда равна 180 градусам. Это свойство смежных углов называется линейной парой углов. Если известно измерение одного смежного угла, можно вычислить измерение другого угла, вычитая это значение из 180 градусов.

Примеры смежных углов можно встретить в различных геометрических фигурах, таких как треугольники, прямоугольники и параллелограммы. Зная свойства смежных углов, можно легко решать задачи по геометрии и находить значения углов в различных фигурах.

Таким образом, смежные углы имеют важное значение в геометрии, и их геометрическое обозначение и измерение позволяют точно определить и вычислить значения этих углов.

Смежные углы: связь с другими типами углов

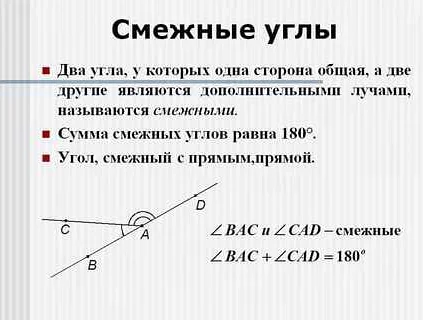
Первый тип углов, с которыми связаны смежные углы, это вертикальные углы. Вертикальные углы образуются при пересечении двух прямых линий и равны друг другу. Если два смежных угла являются вертикальными, то они также равны.

Второй тип углов, с которыми связаны смежные углы, это дополнительные углы. Дополнительные углы образуются двумя углами, сумма которых равна 180 градусов. Если два смежных угла являются дополнительными, то их сумма также равна 180 градусов.

Третий тип углов, с которыми связаны смежные углы, это смежно-внутренние углы. Смежно-внутренние углы образуются при пересечении двух прямых линий и лежат по одну сторону от пересекающейся прямой. Если два смежных угла являются смежно-внутренними, то их сумма равна 180 градусов.

Изучение связи смежных углов с другими типами углов помогает углубить понимание их свойств и использовать их в решении различных математических задач.

Смежные углы: примеры из реальной жизни

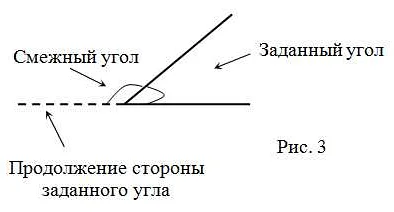
Понимание понятия смежных углов может быть полезно не только в математике, но и в повседневной жизни. Смежные углы можно встретить в различных ситуациях, например, при изучении геометрии зданий или при решении задач на планирование пространства.

Рассмотрим несколько примеров, где смежные углы играют важную роль:

1. Дизайн интерьера

В процессе планирования интерьера помещения важно учитывать углы между стенами, мебелью и другими элементами. Например, при размещении двух диванов под прямым углом, углы между спинками этих диванов будут смежными.

2. Архитектура

При проектировании зданий архитекторы часто используют смежные углы для создания гармоничных и эстетически приятных форм. Например, при построении многоугольного плана здания, углы между сторонами будут смежными.

3. Укладка плитки

При укладке плитки на пол или стены важно учитывать углы между плитками. Смежные углы могут помочь создать ровный и прочный покрытие. Например, углы между укладываемыми плитками в виде квадрата будут смежными.

Это лишь некоторые примеры, где знание смежных углов может быть полезным. В общем случае, понимание этого понятия может помочь в анализе и решении различных задач в повседневной жизни.

Смежные углы: приложения в геометрии

Первое применение смежных углов связано с параллельными линиями. Если две прямые линии пересекаются, то образовавшиеся смежные углы будут равными. Это свойство можно использовать для нахождения углов при решении задач на нахождение неизвестных углов в треугольниках, параллелограммах и других фигурах.

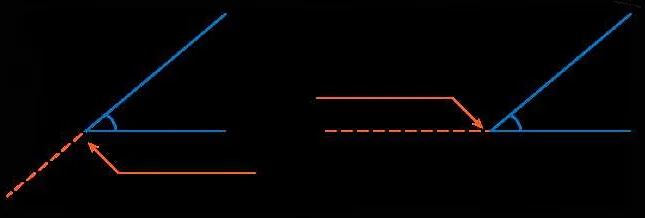
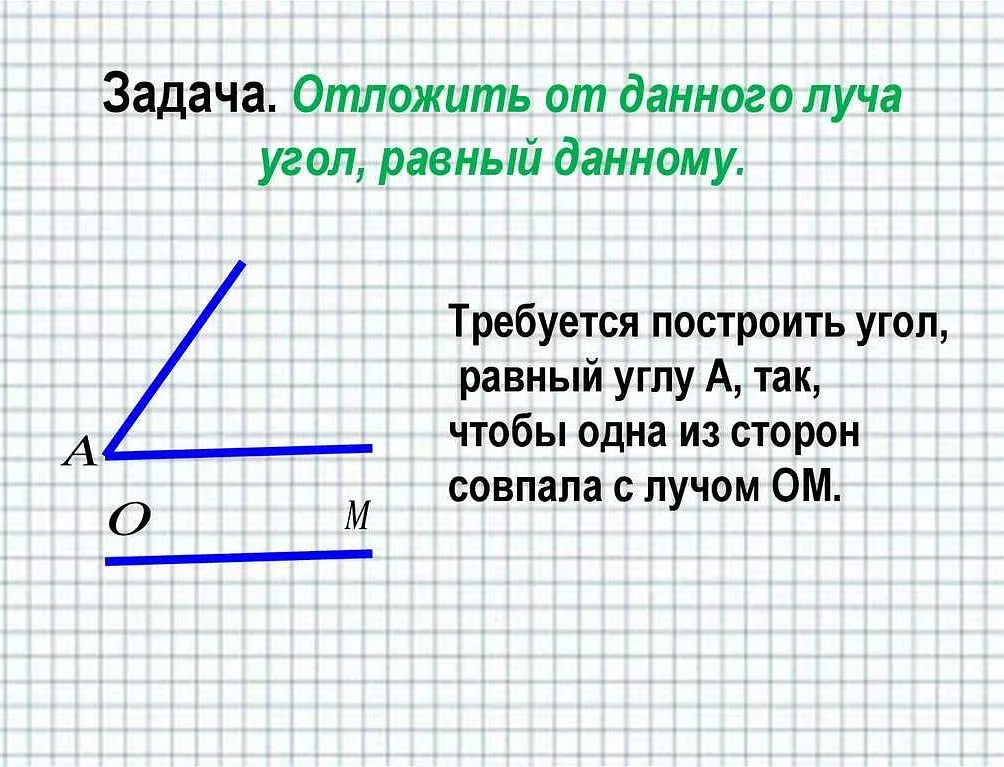
Второе применение смежных углов связано с конструкцией параллельных линий. Если известно, что две прямые линии пересекаются и образуют смежные углы, то можно построить параллельную прямую, проходящую через заданную точку. Для этого нужно найти равные смежные углы и построить прямую, проходящую через заданную точку и образующую те же углы с двумя пересекающимися прямыми.

Третье применение смежных углов связано с измерением углов. Смежные углы могут быть использованы для нахождения неизвестных углов при измерении с помощью угломера или гониометра. Если известен один из смежных углов, то можно найти значение другого угла, используя свойство равенства смежных углов.

В заключение, смежные углы являются важным инструментом в геометрии и находят широкое применение в решении задач на нахождение углов, построение параллельных линий и измерение углов. Понимание свойств и приложений смежных углов помогает улучшить навыки решения геометрических задач.

Вопрос-ответ:

Что такое смежные углы?

Смежные углы — это два угла, которые имеют общую сторону и общую вершину и лежат по разные стороны от общей стороны.

Какие свойства имеют смежные углы?

Смежные углы имеют несколько свойств. Во-первых, сумма смежных углов равна 180 градусам. Это значит, что если угол А и угол В являются смежными, то их сумма будет равна 180 градусам. Во-вторых, если угол А и угол В являются смежными, то угол А и угол В образуют линейную пару углов, то есть сумма их угловых величин равна 180 градусам.

Можно ли смежные углы назвать смежными вершинами?

Нет, нельзя. Смежные углы могут иметь общую вершину, но называть их смежными вершинами не правильно. Смежные углы — это углы, имеющие общую сторону и общую вершину, но смежные вершины — это вершины, лежащие на одной линии.

Какие примеры смежных углов можно привести?

Примерами смежных углов могут служить углы внутри треугольника. Например, если у нас есть треугольник АВС, то угол ВАС и угол ВСА будут смежными углами. Еще одним примером могут быть углы при пересечении двух прямых. Если две прямые пересекаются, то углы, образованные этим пересечением, будут смежными углами.

Смежные углы: использование в архитектуре

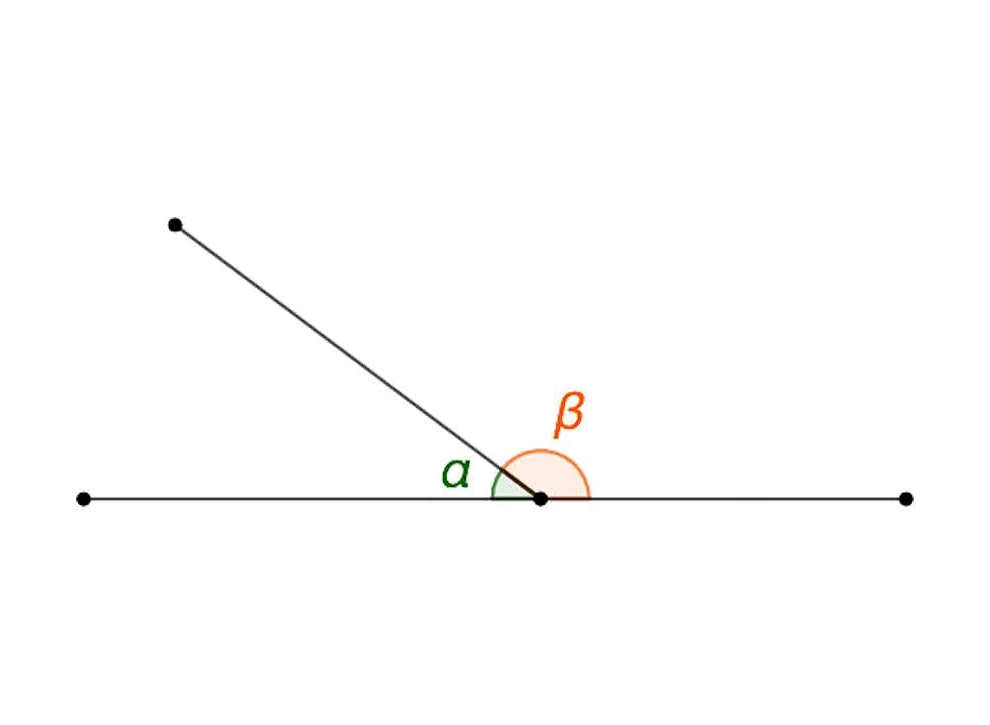
Одним из примеров использования смежных углов в архитектуре являются фасады зданий. Часто архитекторы используют смежные углы для создания симметричных и сбалансированных фасадов. Пары смежных углов могут быть использованы для создания интересных форм и композиций.

Кроме того, смежные углы могут быть использованы для создания объемных архитектурных элементов, таких как башни, колонны и арки. Эти элементы могут иметь сложные формы, состоящие из нескольких смежных углов, что придает им уникальный и запоминающийся вид.

Смежные углы также широко используются для создания переходов и соединений между различными частями зданий. Например, они могут быть использованы для создания закругленных углов зданий, что делает их более безопасными и эстетически приятными.

В целом, использование смежных углов в архитектуре позволяет создавать уникальные и привлекательные конструкции. Они способствуют созданию гармонии, симметрии и эстетической привлекательности зданий.

Видео по теме: