Что такое смежный угол в математике

Смежный угол в математике — это пара углов, имеющих общую сторону и вершину, расположенные по обе стороны общей стороны. Узнайте, как определить смежные углы, и как они используются в геометрии.

Смежный угол — это один из основных понятий в геометрии, которое широко используется при изучении углов и их свойств. Смежные углы могут быть найдены в различных фигурах и иметь разные значения, но их определение остается неизменным: это углы, которые имеют общую сторону и общую вершину.

Определение смежных углов можно привести на примере прямой, разделенной на две части. Таким образом, всегда будет существовать две пары смежных углов, где одна пара является суммой двух углов, равной 180°. Другая пара смежных углов будет дополнительной к первой паре и также равна 180°.

Например, рассмотрим прямую линию, которая разделена на две равные части. В этом случае каждая пара смежных углов будет состоять из двух углов, равных 90°. Таким образом, сумма каждой пары смежных углов будет равна 180°.

Смежные углы широко используются в геометрии для решения задач и доказательства различных теорем. Знание и понимание свойств смежных углов помогает анализировать и решать задачи, связанные с углами, и строить геометрические доказательства. Поэтому понимание определения и примеров смежных углов является важным элементом в освоении геометрии.

Что такое смежный угол в математике?

Смежные углы образуются, когда две прямые линии пересекаются. Они могут быть расположены как на плоскости, так и в трехмерном пространстве.

Смежные углы могут быть разного вида:

1. Смежные углы смежного угла. Это пара углов, которые находятся по разные стороны от общего угла. Они дополняют друг друга и сумма их мер равна 180 градусов.
2. Смежные углы вертикально-дополнительного угла. Это пара углов, которые находятся по разные стороны от общей стороны и образуют линию с вертикальным углом. Они равны и сумма их мер также равна 180 градусов.
3. Смежные углы дополняющего угла. Это пара углов, которые находятся по разные стороны от общей стороны и образуют линию с углом, дополняющим другой угол. Сумма их мер также равна 180 градусов.

Смежные углы играют важную роль в геометрии и могут быть использованы для решения различных задач, таких как вычисление неизвестных углов или нахождение параллельных линий.

Примеры смежных углов:

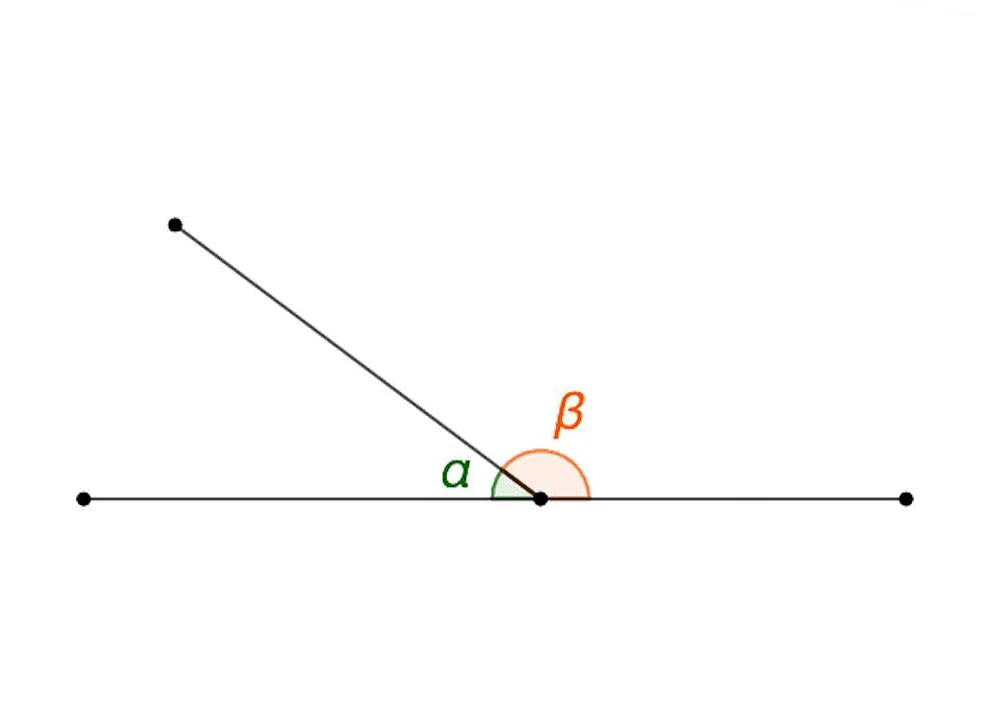
На рисунке ниже показан пример двух смежных углов. Угол AOB и угол BOC являются смежными углами, так как они имеют общую сторону OB и общую вершину O. Они находятся по разные стороны от общей стороны и не пересекаются.

Определение смежного угла

Смежные углы могут быть как прямыми, так и непрямыми. Прямые смежные углы составляют сумму 180 градусов, так как они являются смежными углами с дополнительным углом. Непрямые смежные углы составляют сумму 360 градусов, так как они являются смежными углами с обратным углом.

Смежные углы являются важным понятием в геометрии и используются для решения различных задач, таких как нахождение измерений углов, построение фигур и доказательство теорем.

Смежные углы: основные характеристики

Основные характеристики смежных углов:

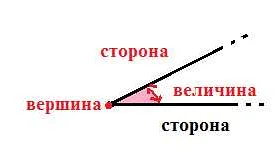
1. Смежные углы всегда имеют общую вершину. Вершина является точкой пересечения двух лучей, которые образуют угол.
2. Смежные углы имеют одну общую сторону. Сторона образует границу между двумя смежными углами.
3. Сумма смежных углов всегда равна 180 градусов. Если известна величина одного смежного угла, то второй угол можно найти, вычитая значение из 180.
4. Смежные углы обладают свойством, что если один из углов является прямым (равен 90 градусам), то второй угол также будет прямым.

Знание основных характеристик смежных углов помогает в решении задач по геометрии и облегчает понимание связей между углами в фигурах.

Примеры смежных углов

Смежные углы могут быть найдены в различных геометрических фигурах и конструкциях. Вот несколько примеров:

1. В прямоугольнике углы, которые расположены рядом и имеют общую сторону, являются смежными. Например, углы A и B на рисунке:

   A——B
   | |
   | |
   C——D

2. В параллелограмме противоположные углы также являются смежными. Например, углы A и B на рисунке:

   A——-B
   / \
   / \
   D————-C

3. В треугольнике смежные углы образуются при сопряжении двух сторон. Например, углы A и B на рисунке:

   A
   / \
   / \
   B——C

4. Вертикальные углы также являются смежными. Это углы, которые образуются при пересечении двух прямых линий. Например, углы 1 и 2 на рисунке:

   1————2
   | |
   | |
   3————4

Это лишь некоторые примеры смежных углов. В реальном мире вы можете найти множество других примеров, где смежные углы используются для решения задач и анализа геометрических объектов.

Смежный угол: свойства

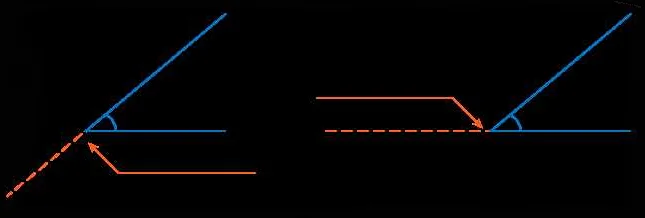
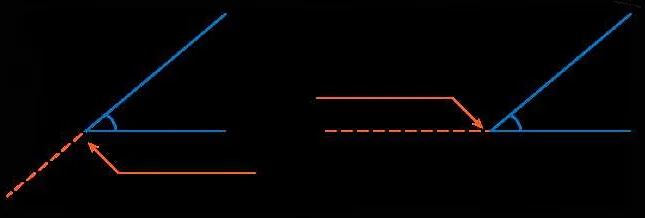
Свойства смежных углов:

1. Сумма смежных углов равна 180 градусам. Если углы А и В являются смежными, то А + В = 180°. Это свойство можно использовать для вычисления значения одного из углов, если известно значение другого.
2. Смежные углы могут быть смежными дополнительными. Дополнительные углы — это пара углов, сумма которых равна 180 градусам. Если углы А и В являются смежными дополнительными, то А + В = 180°. Это свойство позволяет находить один угол, зная значение другого.
3. Смежные углы могут быть вертикальными. Вертикальные углы — это пара углов, расположенных напротив друг друга при пересечении двух прямых линий. Если углы А и В являются вертикальными, то они равны между собой. Это свойство позволяет находить значения углов при решении геометрических задач.
4. Смежные углы могут быть смежными с понятием прямого угла. Прямой угол — это угол, равный 90 градусам. Если углы А и В являются смежными с прямым углом, то А + В = 90°. Это свойство позволяет находить значения углов, связанных с прямыми линиями и плоскостями.

Знание свойств смежных углов позволяет более эффективно работать с геометрическими задачами и делает вычисления более простыми и удобными.

Как определить смежные углы?

1. Убедитесь, что два угла имеют общую вершину. Вершина — это точка, в которой пересекаются две стороны угла.
2. Убедитесь, что два угла имеют общую сторону. Сторона — это линия, которая соединяет две вершины угла.
3. Убедитесь, что два угла не пересекаются и не имеют других общих точек, кроме вершины и стороны.

Если все эти условия выполняются, то два угла являются смежными. Смежные углы могут быть разных размеров и положений, но они всегда имеют общую вершину и общую сторону.

Применение смежных углов в реальной жизни

Понимание понятия смежных углов может быть полезно не только в математике, но и в реальной жизни. Знание этой концепции может помочь нам в решении различных задач и проблем в повседневной жизни.

Например, знание смежных углов может быть полезным при проведении строительных работ. Представим, что мы хотим построить прямой угол между двумя стенами в комнате. Зная, что сумма смежных углов равна 180 градусов, мы можем использовать эту информацию для правильной установки стен и получения точного угла.

Также, смежные углы могут быть полезными при решении задач в геодезии. Например, при измерении угловых отклонений между линиями или структурами на местности. Зная, что сумма смежных углов равна 180 градусов, мы можем использовать эту информацию для определения точного угла и выполнения точных измерений.

Кроме того, понимание смежных углов может быть полезным при решении головоломок и задач по логике. Зная свойства смежных углов, мы можем легко увидеть закономерности и сделать правильные выводы, что поможет нам в решении задачи.

Таким образом, понимание смежных углов имеет практическое применение в различных областях нашей жизни. Оно помогает нам решать задачи, проводить измерения и логические рассуждения, а также строить и ремонтировать различные объекты.

Видео по теме:

Что такое смежные углы?

Смежные углы — это два угла, которые имеют общую сторону и общую вершину. Они расположены на одной прямой и не пересекаются друг с другом.

Как можно определить смежные углы?

Для определения смежных углов нужно найти два угла, которые имеют одну общую сторону и общую вершину.

Можно ли найти смежные углы вне прямой?

Нет, смежные углы всегда находятся на одной прямой. Они не могут быть расположены вне прямой.

Что такое смежный угол?

Смежный угол — это два угла, которые имеют общую сторону и общую вершину. Они расположены рядом друг с другом, и их сумма равна 180 градусам.