Компьютерная математическая модель в информатике: что это и зачем нужно знать

Компьютерная математическая модель – это абстрактное описание объекта или процесса в виде математических формул и алгоритмов, реализованных на компьютере для получения прогнозов и исследований. Узнайте, как она применяется в информатике и как создать свою собственную математическую модель.

В информатике, компьютерная математическая модель является одним из важнейших инструментов, использующихся для создания и анализа программных систем, прогнозирования поведения и разработки алгоритмов. Она представляет собой математическое описание реального процесса или системы, которое позволяет оперировать данными и проводить эксперименты для получения новой информации.

Разработка компьютерных моделей позволяет проводить теоретические исследования без необходимости создания физических экспериментов, что позволяет существенно сократить затраты на проведение исследований и оптимизировать их результаты. Компьютерные модели используются для симуляции различных процессов и явлений, от экономических систем до биологических и физических процессов.

Кроме этого, компьютерные модели играют важную роль в научных и инженерных исследованиях в таких областях, как аэрокосмическое проектирование, медицинская и биологическая наука, климатология, энергетика, финансы и многие другие. Компьютерные модели также позволяют проводить испытания новых материалов, прогнозировать результаты экспериментов и анализировать различные системы в условиях, когда физические эксперименты просто невозможны или принципиально невыгодны.

Общие принципы компьютерной математической модели

Компьютерная математическая модель – это средство, которое позволяет создавать прогнозы, оценки и анализы процессов и явлений, происходящих в реальном мире. Ее основной целью является сокращение затрат и повышение точности решения задач. Кроме того, она позволяет производить серию испытаний, которые не всегда возможно выполнить в реальности.

Общие принципы компьютерной математической модели – это основа ее работы. Она строится на основе логически связанных систем и отношений между компонентами модели. Ее создание начинается с анализа задачи, которую необходимо решить, а затем описания процесса или явления на языке математических формул.

Компьютерная математическая модель строится на основе изучения и анализа данных. Она способна адекватно отображать поведение объектов, которые нужно моделировать, позволяет имитировать динамику процессов и воздействовать на них различными способами.

Одним из главных принципов компьютерной математической модели является ее верификация. Проверка моделирования должна быть проведена на основе сопоставления результатов работы модели с реальными наблюдениями. Кроме того, необходимо проверить работу модели на различных задачах и с разными начальными установками.

Компьютерная математическая модель – это важный инструмент для научных исследователей, инженеров и экономистов, который позволяет оптимизировать процессы и прогнозировать поведение объектов и систем в будущем.

Задачи, которые решает компьютерная математическая модель

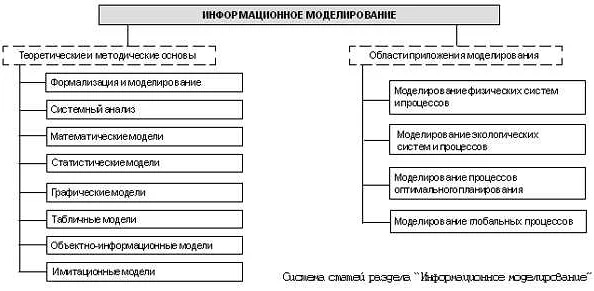
Компьютерная математическая модель – это очень мощный инструмент, который позволяет решать множество задач в различных областях науки и техники. Рассмотрим несколько примеров задач, которые может решать компьютерная математическая модель:

• Разработка новых технологий и технических решений. Компьютерная математическая модель позволяет исследовать и анализировать сложные технические системы, прогнозировать их поведение и оптимизировать параметры для улучшения характеристик.
• Медицинские исследования. Компьютерная математическая модель может помочь в разработке новых препаратов, проектировании медицинских устройств и оценке рисков в области здравоохранения.
• Экономические расчеты. Компьютерная математическая модель может применяться для анализа экономической ситуации, определения оптимальных стратегий инвестирования, прогнозирования инфляции и других важных факторов.
• Химические исследования. Компьютерная математическая модель может использоваться для моделирования новых химических реакций и материалов, определения их свойств и экологических последствий.

Это – лишь некоторые примеры задач, которые может решать компьютерная математическая модель. Его возможности весьма разнообразны и зависят от области применения и специфики задачи.

Виды компьютерной математической модели

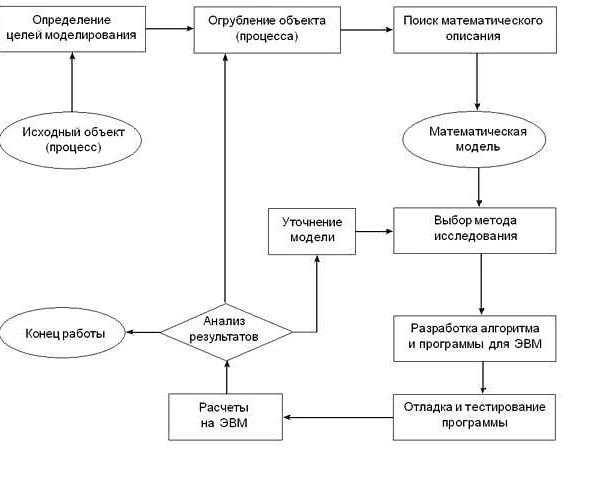
Существует несколько различных видов компьютерных математических моделей в информатике, каждая из которых обладает своими уникальными свойствами и сферами применения. Некоторые из наиболее распространенных типов моделей включают в себя следующие:

1. Статические модели — это модели, которые описывают систему или процесс в конкретный момент времени. Они могут использоваться для анализа и управления системами, которые не изменяются во времени.
2. Динамические модели — это модели, которые представляют собой систему или процесс, который меняется с течением времени. Они предназначены для анализа и оптимизации динамических процессов.
3. Дискретные модели — это модели, которые описывают систему или процесс, состоящий из конечного числа дискретных состояний или событий. Они широко используются в области симуляции и анализа систем массового обслуживания.
4. Непрерывные модели — это модели, которые представляют собой систему, которая изменяется непрерывно во времени. Они используются для анализа и моделирования физических систем, таких как электрические цепи и механические системы.
5. Аналитические модели — это модели, которые описывают систему или процесс с помощью уравнений и других математических методов. Они обычно используются для анализа и предсказания поведения системы.

Выбор подходящего типа модели зависит от конкретных требований и сферы применения. Однако, все модели имеют общую цель — помочь понять и оптимизировать сложные системы и процессы.

Процесс создания компьютерной математической модели

Создание компьютерной математической модели — это сложный и многоэтапный процесс, включающий в себя несколько основных этапов. Первый этап — это формулирование задачи, определение ее целей и параметров. Необходимо определить какие процессы и явления будут описываться моделью, какие параметры они будут иметь и какие результаты необходимо получить из моделирования.

На втором этапе эксперты должны выбрать математическую модель, которая наилучшим образом соответствует поставленной задаче. Эта модель определяет, какие законы и уравнения будут использоваться для описания конкретной ситуации или процесса.

Далее необходимо собрать данные, которые будут использоваться при построении модели. В зависимости от характера модели, это могут быть данные из экспериментов, измерений или опросов. Они используются для оценки параметров модели, подтверждения ее корректности и достоверности.

После сбора данных, специалисты приступают к построению модели. Этот процесс включает в себя определение начальных значений и уравнений, используемых компьютерной программой для имитации процесса.

Наконец, специалисты приступают к тестированию модели. Это происходит за счет сравнения результата, полученного с помощью моделирования, со значениями, полученными в реальности. Если модель соответствует реальности, она может быть использована для принятия решений, прогнозирования или анализа ситуаций.

Создание компьютерных математических моделей является кропотливым процессом, включающим в себя множество этапов и тщательную проверку. Однако разработка хорошей модели способна не только экономить время и увеличивать точность предсказаний, но и помогать принимать более обоснованные решения в условиях неопределенности и неизвестности.

Примеры использования компьютерной математической модели в информатике

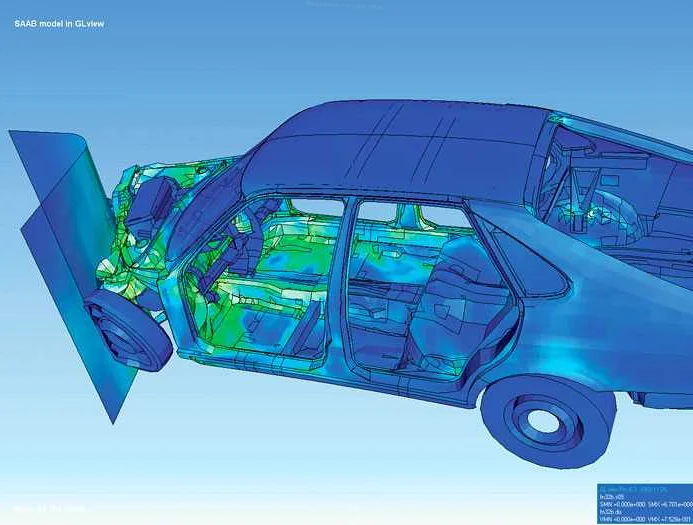
1. Моделирование сетей связи

Компьютерные математические модели могут использоваться для моделирования и анализа сетей связи. Это помогает инженерам и администраторам сети оптимизировать сетевую инфраструктуру, предотвращать сбои и улучшать скорость передачи данных.

2. Прогнозирование погоды

Компьютерные математические модели могут также использоваться для прогнозирования погоды. Они анализируют огромное количество данных о погоде с помощью сложных алгоритмов и формул, что позволяет предсказывать изменения в погодных условиях с высокой точностью.

3. Симуляция физических процессов

С помощью компьютерных математических моделей можно симулировать различные физические процессы, такие как динамика жидкостей, гравитация, электромагнитные поля и т.д. Это позволяет исследовать и предсказывать реакцию системы на различные воздействия и оптимизировать ее работу.

4. Моделирование финансовых рынков

Компьютерные математические модели могут использоваться для предсказания поведения финансовых рынков и построения оптимальных портфелей инвестиций. Это помогает инвесторам и финансистам принимать более обоснованные решения и уменьшать риски.

5. Анализ данных и машинное обучение

Компьютерные математические модели используются в анализе данных и машинном обучении для построения алгоритмов, которые могут классифицировать, распознавать и обрабатывать большой объем информации автоматически. Это облегчает рутинную работу и улучшает эффективность бизнес-процессов.

Преимущества и недостатки компьютерной математической модели

Преимущества:

• Позволяет проводить разнообразный анализ исходных данных;
• Ускоряет процесс принятия решений;
• Создает возможность проводить эксперименты в неопределенных ситуациях;
• Позволяет сократить затраты на организацию процессов;
• Увеличивает эффективность производства;
• Уменьшает риски ошибок при принятии решений в рискованных ситуациях.

Недостатки:

• Модель создает идеализированную картину реальности, и в реальности могут возникнуть явления непредвиденные моделью;
• Точность модели зависит от точности входных данных, которые могут быть неточными;
• Существует риск переоценки значимости параметров при построении модели;
• Моделирование является недешевым процессом, особенно при необходимости использования большого количества данных и вычислительных ресурсов.

В целом, компьютерная математическая модель является полезным инструментом для анализа и принятия решений в различных сферах деятельности, однако важно учитывать недостатки этого инструмента и аккуратно проводить анализ данных для получения максимально точной и полной информации.

Контроль качества и верификация компьютерной математической модели

В процессе разработки компьютерной математической модели необходимо провести контроль качества и верификацию, чтобы убедиться в ее правильности и соответствии заданным требованиям.

Контроль качества включает проверку программного кода на наличие ошибок, оптимизацию алгоритмов и устранение проблем с производительностью. Он также может включать различные виды тестирования модели, например, функциональное тестирование, тестирование нагрузки и тестирование безопасности.

Верификация модели означает проверку того, что она достаточно точно представляет реальный объект или процесс. Это может включать анализ и сравнение модели с фактическими данными, выполнение статистических тестов и оценку ее точности и надежности.

Важным аспектом контроля качества и верификации является создание документации, описывающей результаты тестирования и верификации модели, а также ее основные характеристики и ограничения. Это помогает обеспечить прозрачность процесса и повышение доверия к модели.

Инструменты для работы с компьютерной математической моделью

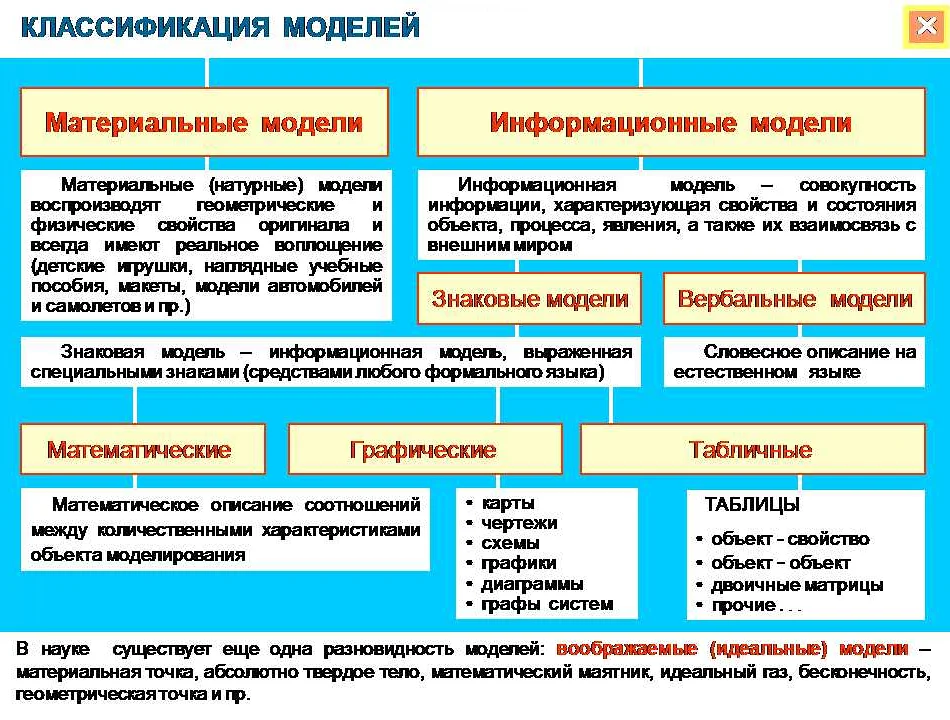
1. Различные языки программирования: Для создания компьютерных математических моделей специалистам необходимо владеть языками программирования. Наиболее распространенными языками программирования для моделирования являются: MATLAB, Mathematica, Python, R. Они предоставляют мощные инструменты для решения математических задач, включая методы оптимизации, статистический анализ и обработку данных.

2. Системы компьютерной алгебры: Системы компьютерной алгебры (КА) предназначены для выполнения математических операций символьно, включая производные, интегралы, уравнения и системы уравнений. Примеры таких систем включают Maple, Mathematica, Maxima и Sage. Системы КА могут помочь специалистам в процессе моделирования и анализа результатов.

3. Графические пакеты: Графические пакеты предназначены для создания визуальных представлений математических моделей и результатов их анализа. Наиболее распространенные графические пакеты включают Gnuplot, Matplotlib и Plotly. Они могут успешно применяться для визуализации данных и построении графиков.

4. Симуляторы: Симуляторы используются для имитации моделей и предсказаний поведения реальных систем. Серьезными примерами могут являться транспортные системы и экономические процессы. Примеры таких симуляторов включают AnyLogic, Arena и FlexSim. С их помощью можно предсказать результаты новых стратегий и планов их реализации.

Таким образом, широкий спектр инструментов доступен специалистам для создания, анализа и визуализации компьютерных математических моделей. Важно выбрать правильные инструменты в соответствии с задачами, которые необходимо решить.

Применение компьютерной математической модели в решении бизнес-задач

Современный бизнес невозможен без использования математических методов и моделей. Компьютерные математические модели (КММ) позволяют решать сложные задачи, оптимизировать бизнес-процессы и принимать взвешенные решения.

Одной из наиболее распространенных областей применения КММ в бизнесе является прогнозирование продаж. С помощью математических моделей можно определить, какие товары будут наиболее востребованы в будущем, что позволит оптимизировать производственную линию, складскую логистику и повысить эффективность маркетинговых кампаний.

КММ могут также помочь в решении задач кредитного скоринга и оценки рисков. Анализ данных по кредитной истории клиентов позволяет определить вероятность невозврата кредита и более точно оценить кредитоспособность заемщиков. Кроме того, КММ позволяют сократить время, затрачиваемое на обработку больших объемов информации и снизить риски финансовых потерь.

В области логистики КММ могут помочь оптимизировать маршруты доставки и управлять складскими запасами. Моделирование бизнес-процессов позволяет предприятиям находить сильные и слабые стороны своей деятельности и улучшать эффективность работы.

Таким образом, КММ играют важную роль в решении бизнес-задач и помогают предприятиям быть более эффективными и конкурентоспособными на рынке.

Будущее компьютерной математической модели в информатике

Современная информационная среда ставит перед компьютерными математическими моделями все более и более сложные задачи. Кроме того, технологии развиваются с огромной скоростью, поэтому модели должны быть гибкими и адаптивными.

Одним из направлений развития моделей является использование искусственного интеллекта и машинного обучения. Результаты исследований в этой области уже применяются в таких областях, как медицина, финансы, производство, наука.

Другим направлением является интеграция моделей в большие информационные системы. Модели должны стать частью крупных интернет-платформ и систем, чтобы обеспечивать более точный анализ и прогнозирование данных.

Важно отметить, что развитие моделей не может идти отдельно от технологического продвижения в целом. Продолжительная жизнеспособность моделей зависит от того, насколько они будут способны адаптироваться к новым вычислительным технологиям, языкам программирования и стандартам связи.

• Поэтому будущее компьютерных математических моделей связано с:
• развитием искусственного интеллекта и машинного обучения;
• интеграцией моделей в крупные информационные системы;
• адаптивностью к новым технологиям и стандартам связи.

Вопрос-ответ:

Что такое компьютерная математическая модель?

Компьютерная математическая модель — это модель, которая создается с помощью математического аппарата и предназначена для исследования реальных систем или процессов. Она позволяет провести эксперименты, не нанося ущерба окружающей среде и не требуя больших затрат времени и средств. Простыми словами, это такая модель, которую можно использовать на компьютере для моделирования процессов реального мира.

Какие задачи можно решить с помощью компьютерных математических моделей?

Компьютерные математические модели могут использоваться для решения различных задач: от простых математических вычислений до сложных исследований процессов в экономике, биологии, физике и т.д. Например, они могут помочь предсказать погоду, оценить эффективность медицинских препаратов, определить оптимальный маршрут для транспорта и многое другое.

Какие инструменты используются для создания компьютерных математических моделей?

Для создания компьютерных математических моделей часто используются языки программирования, такие как Python, MATLAB, C++, Java и другие. Также могут использоваться специальные программные обеспечения, предназначенные для моделирования, например, AnyLogic, Simulink.

Какова роль компьютерных математических моделей в информатике?

Компьютерные математические модели очень важны в информатике. Они позволяют оптимизировать процессы и создавать новые технологии. Например, моделирование процессов в телекоммуникациях позволяет увеличить скорость передачи данных и улучшить качество связи. Или моделирование работы компьютерных сетей может помочь обеспечить их стабильность и защиту от возможных угроз.

Каковы преимущества использования компьютерных математических моделей?

Основное преимущество использования компьютерных математических моделей заключается в том, что они позволяют экономить ресурсы при проведении исследований и экспериментов. Также они могут сократить время, необходимое для получения результатов. Кроме того, компьютерные математические модели позволяют исследовать процессы, которые не могут быть изучены в реальном мире, например, из-за опасности для здоровья или жизни людей.

Как создать математическую модель в информатике?

Для создания математической модели в информатике необходимо выполнить следующие шаги: определить цель моделирования, выбрать математические методы, разработать алгоритм моделирования, написать код модели на выбранном языке программирования, провести тестирование и анализ полученных результатов.

Какова роль компьютерных математических моделей в науке и исследованиях?

Компьютерные математические модели играют огромную роль в науке и исследованиях. Они позволяют исследовать сложные процессы и предсказывать их поведение в различных условиях. Например, они широко используются в биологии и медицине для изучения механизмов заболеваний и разработки новых лекарств. А также в физике, геологии и астрономии для изучения свойств материи и прогнозирования космических явлений.

Видео по теме: