Что такое тождество в математике 6 класс

В статье рассказывается о понятии тождества в математике для учащихся 6 класса. Описываются основные определения, приводятся примеры и объясняется, как использовать тождество в решении математических задач.

Тождество – это математическое равенство, которое выполняется для всех значений переменных. В других словах, тождество верно для любого значения переменной или выражения. Тождества в математике широко используются для доказательства различных утверждений и решения уравнений.

Тождество может быть записано в виде равенства с знаком тождества (=), где выражения справа и слева от знака равенства равны для всех значений переменных. Например, тождество а+б=б+а верно для любых значений переменных а и б.

Пример: для любого числа а тождество а+0=а верно, так как при сложении любого числа с нулем получается то же самое число.

Тождество в математике 6 класс очень важно для понимания и применения различных математических концепций. Умение работать с тождествами позволяет ученикам лучше разбираться в математических задачах и решать их более эффективно.

Что такое тождество в математике?

Тождество можно записать в виде равенства двух выражений, используя знак «=»: A = B, где A и B — выражения, которые являются равными друг другу для любых значений переменных.

Примеры тождеств:

ТождествоРавенствоЗначение переменных

а + b = b + a	2 + 3 = 3 + 2	a = 2, b = 3
а * (b + c) = a * b + a * c	2 * (3 + 4) = 2 * 3 + 2 * 4	a = 2, b = 3, c = 4

В примерах выше тождества выполняются для любых значений переменных, поэтому они истинны. Тождества являются важным понятием в математике и используются для доказательства других математических утверждений и преобразования выражений.

Основные свойства тождеств

Вот некоторые основные свойства тождеств:

1. Свойство рефлексивности: для любого числа a справедливо тождество a = a.
2. Свойство симметричности: если a = b, то также и b = a.
3. Свойство транзитивности: если a = b и b = c, то также и a = c.
4. Свойство замены: если a = b, то a можно заменить на b в любом выражении.
5. Свойство тождественности: если a = b, то a можно заменить на b в любом уравнении.
6. Свойство обратимости: если a = b, то также и -a = -b и 1/a = 1/b (при условии, что a и b не равны нулю).
7. Свойство дистрибутивности: a * (b + c) = a * b + a * c.

Эти свойства позволяют упростить и преобразовать уравнения, а также упростить выражения, делая их более понятными и легкими для решения.

Как доказывать тождества в математике?

1. Аксиомы и определения: Перед тем, как приступить к доказательству тождества, необходимо внимательно изучить аксиомы и определения, которые формируют основу математической теории. Они помогут понять, какие операции и правила можно применять при доказательстве тождества.

2. Использование свойств операций: Для доказательства тождества можно применять свойства операций, такие как коммутативность, ассоциативность, дистрибутивность и др. Например, для доказательства тождества (a + b) + c = a + (b + c), можно воспользоваться ассоциативностью сложения.

3. Приведение выражений к одному виду: В некоторых случаях требуется привести выражения, стоящие в левой и правой частях тождества, к одному виду. Для этого можно использовать свойства операций и алгебраические преобразования. Например, для доказательства тождества (a + b)^2 = a^2 + 2ab + b^2, можно раскрыть скобки в левой части и привести подобные слагаемые.

4. Использование равенств: Для доказательства тождества часто используются известные равенства и свойства чисел. Например, чтобы доказать тождество a(b + c) = ab + ac, можно воспользоваться распределительным законом умножения относительно сложения.

5. Использование математической индукции: В некоторых случаях доказательство тождества может быть проведено с использованием метода математической индукции. Этот метод основан на проверке истинности утверждения для базового случая (обычно для n = 1) и переходе от одного случая к другому.

6. Запись доказательства: После проведения доказательства тождества важно записать его таким образом, чтобы было понятно, какие операции и правила были использованы. Это поможет другим людям и вам самим лучше понять и запомнить процесс доказательства.

Доказательство тождеств в математике требует внимания к деталям и логическому мышлению. С опытом и практикой вы сможете лучше разбираться в математических операциях и правилах, что поможет вам успешно доказывать тождества и решать сложные задачи.

Примеры простых тождеств

Пример 1: Тождество умножения на единицу.

Для любого числа a выполняется равенство:

a * 1 = a

Это тождество говорит нам, что умножение числа на единицу не меняет его значение.

Пример 2: Тождество сложения нуля.

Для любого числа a выполняется равенство:

a + 0 = a

Это тождество говорит нам, что сложение числа с нулем не меняет его значение.

Пример 3: Тождество коммутативности сложения.

Для любых чисел a и b выполняется равенство:

a + b = b + a

Это тождество говорит нам, что порядок слагаемых в сумме не влияет на ее значение.

Это лишь несколько примеров простых тождеств, которые очень полезны при решении математических задач. При изучении тождеств важно понимать, что они являются утверждениями, которые верны для всех значений переменных, участвующих в них.

Тождества с использованием алгебраических операций

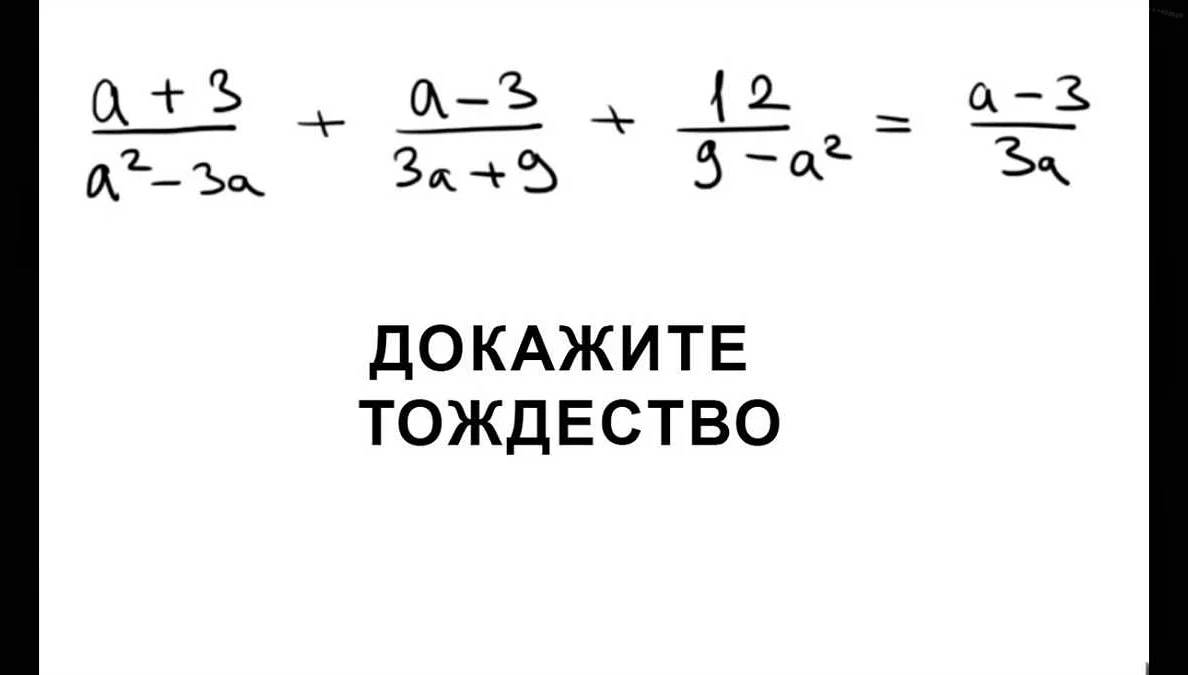
Примером тождества с использованием алгебраических операций может служить тождество для сложения:

a + b = b + a

Это тождество гласит, что результат сложения двух чисел не зависит от порядка, в котором эти числа указаны. Также существуют тождества для других алгебраических операций:

ОперацияТождество

Сложение	a + (b + c) = (a + b) + c
Умножение	a * (b * c) = (a * b) * c
Вычитание	a — (b — c) = (a — b) + c
Деление	a / (b / c) = (a / b) * c

Эти тождества подтверждают, что результаты данных операций не зависят от порядка, в котором они выполняются. Они позволяют упростить вычисления и упорядочить данные в выражениях.

Тождества с использованием геометрических фигур

Одним из известных тождеств с использованием геометрических фигур является формула Пифагора. Она утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Это тождество можно представить следующим образом:

а^2 + b^2 = c^2

где а и b — длины катетов, а c — длина гипотенузы треугольника.

Еще одним примером тождества с использованием геометрических фигур является формула для площади прямоугольника. Она утверждает, что площадь прямоугольника равна произведению длин его сторон. Это тождество можно записать следующим образом:

S = a * b

где S — площадь прямоугольника, а и b — длины его сторон.

Таким образом, тождества с использованием геометрических фигур являются важными математическими утверждениями, которые позволяют решать различные задачи и доказывать другие теоремы.

Решение задач с использованием тождеств

Для решения задач с использованием тождеств можно использовать следующие шаги:

1. Определить, какое тождество подходит для данной задачи.
2. Применить выбранное тождество к исходному выражению.
3. Упростить полученное выражение, используя свойства тождеств.
4. Подставить значения переменных и вычислить решение.

Рассмотрим пример задачи:

ЗадачаРешение

Упростить выражение: 4x + 2x — 5x

1. Выберем тождество a + b + c = a + (b + c). 2. Применим выбранное тождество: 4x + 2x — 5x = 4x + (2x — 5x). 3. Упростим полученное выражение, используя свойства тождеств: 4x + (2x — 5x) = 4x — 3x = x. 4. Подставим значения переменных, например, x = 2: 2. Ответ: x = 2.

Таким образом, использование тождеств позволяет упростить выражения и решить задачи более эффективно.

Видео по теме:

Что такое тождество в математике?

Тождество в математике — это утверждение, которое верно для любых значений переменных, входящих в это утверждение. Оно не зависит от конкретных численных значений, а является верным для всех.

Как доказать, что утверждение является тождеством?

Чтобы доказать, что утверждение является тождеством, необходимо показать, что оно верно для любых значений переменных, входящих в это утверждение. Для этого можно использовать алгебраические преобразования, свойства операций и другие методы решения математических задач.

Зачем нужны тождества в математике?

Тождества в математике играют важную роль, так как они позволяют упростить вычисления и решение математических задач. Они помогают понять основные свойства операций и оперировать с числами и выражениями, не зависимо от их конкретных значений. Тождества также являются основой для дальнейшего изучения алгебры и других разделов математики.