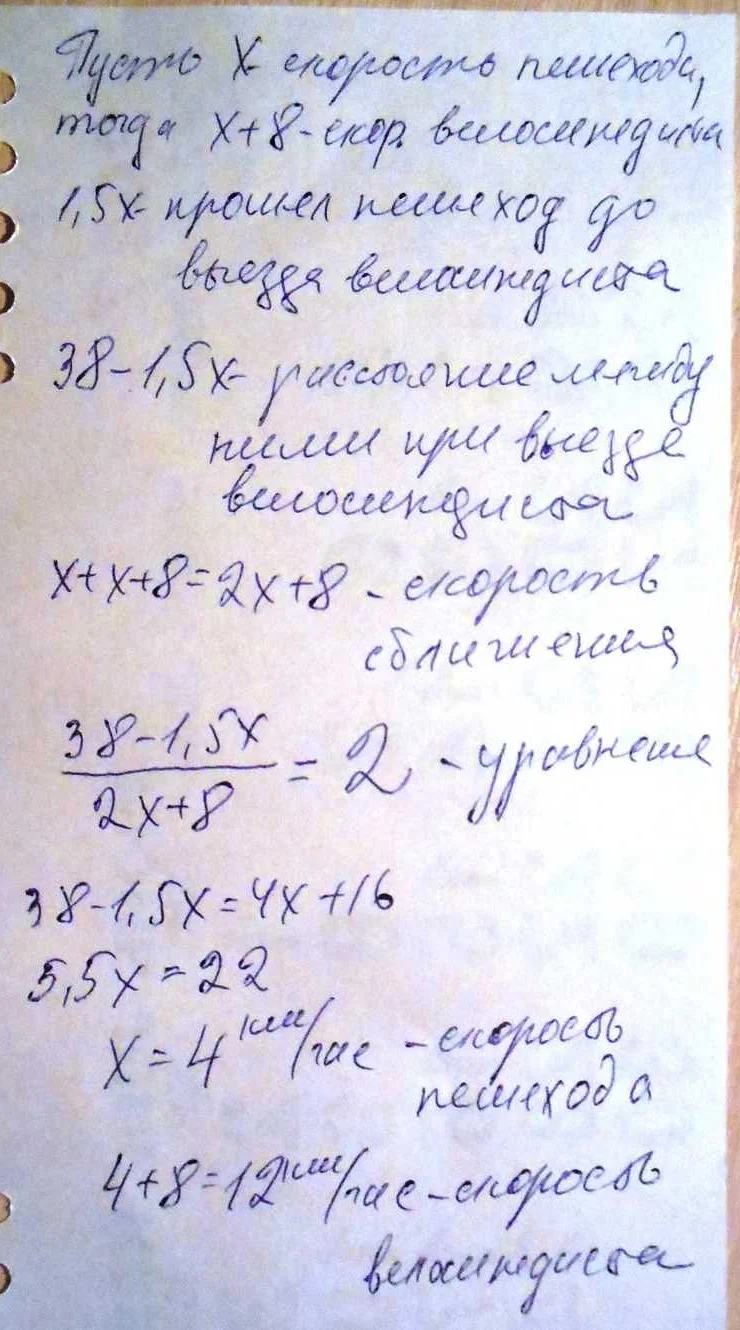Что такое три этапа математического моделирования

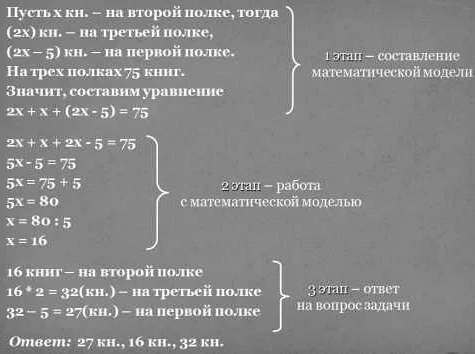
Три этапа математического моделирования — это процесс построения и анализа моделей, использующих математические методы и инструменты. Они включают в себя формулировку проблемы, разработку математической модели и решение полученных уравнений. Узнайте, как эти этапы взаимодействуют и важность каждого из них для успешного моделирования.

Математическое моделирование – это процесс создания и исследования абстрактных моделей, которые представляют объекты и явления реального мира. Оно является неотъемлемой частью современной науки и техники, а также находит широкое применение в различных областях, начиная от физики и экономики, и заканчивая биологией и социологией.

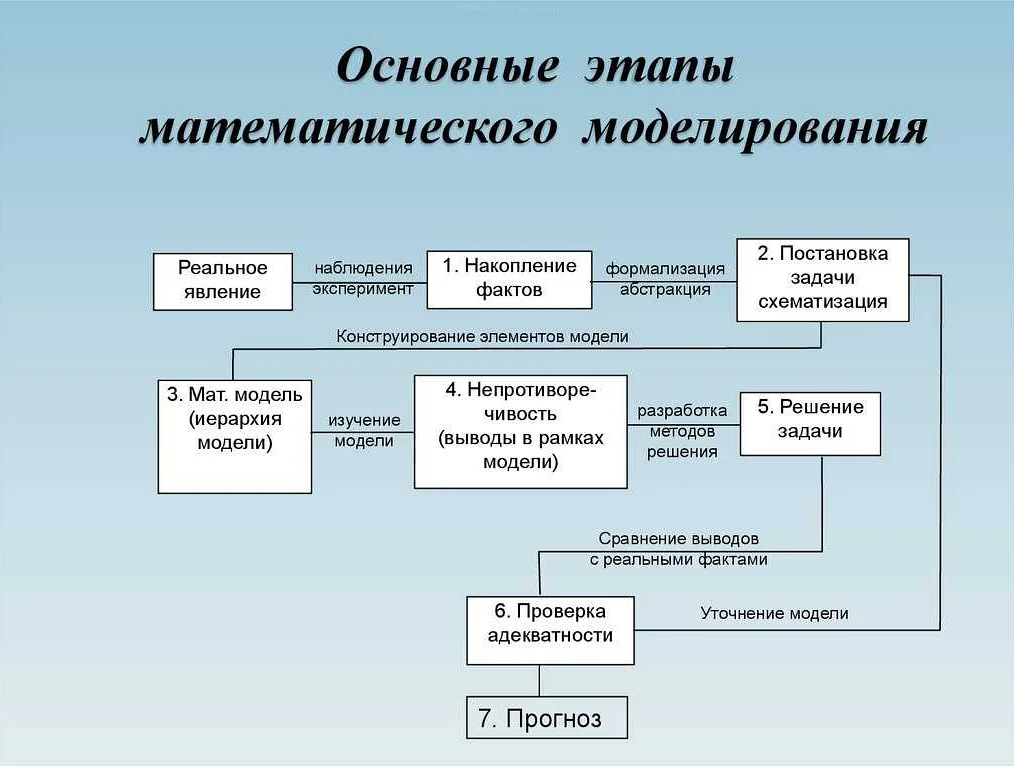
Математическое моделирование обычно проходит через три основных этапа: понятие, методы и применение. На первом этапе, ученые формулируют понятие модели и определяют основные характеристики и свойства объекта или явления, которые они хотят изучить. Затем на втором этапе применяются различные методы, такие как дифференциальные уравнения, статистика и оптимизация, для построения математической модели.

Математическое моделирование построено на использовании различных математических инструментов и теорий. Иногда для создания точной модели требуется разработка новых методов и подходов. На третьем этапе, модель применяется для анализа различных сценариев и предсказания поведения объекта или явления в реальном мире. Это помогает исследователям принимать обоснованные решения и предлагать оптимальные стратегии в различных сферах деятельности.

Математическое моделирование имеет важное значение в современном мире, поскольку позволяет нам лучше понять сложные системы и предсказать их будущее поведение. Оно играет ключевую роль в разработке новых технологий, оптимизации процессов, прогнозировании рисков и принятии обоснованных решений. Понимание трех этапов математического моделирования – понятие, методы и применение – помогает нам строить более точные и эффективные модели, которые в свою очередь способствуют прогрессу и развитию науки и техники.

Понятие математического моделирования

С помощью математического моделирования мы можем изучать сложные системы, предсказывать их поведение и принимать обоснованные решения. Математические модели широко применяются в науке, технике, экономике, физике, биологии и других областях.

Математические модели могут быть различной сложности и уровня абстракции. Одни модели учитывают все детали и особенности системы, включая случайные факторы и неопределенности. Другие модели являются упрощенными и исключают некоторые аспекты системы, чтобы сделать анализ более удобным.

При создании математической модели необходимо учитывать следующие основные принципы:

• Выбор релевантных переменных и параметров, которые описывают систему.
• Формулировка математических уравнений, которые описывают взаимодействия и зависимости между переменными.
• Валидация модели путем сравнения ее результатов с экспериментальными данными.
• Использование модели для проведения анализа, прогнозирования и принятия решений.

Математическое моделирование играет важную роль в науке и практике, позволяя нам лучше понимать и контролировать сложные системы. Оно помогает нам оптимизировать процессы, прогнозировать будущие события и принимать обоснованные решения на основе количественного анализа.

Определение и основные понятия

Основные понятия, связанные с математическим моделированием:

• Модель — упрощенное представление реальной системы или явления при помощи математических символов и отношений.
• Переменные — символы, которые представляют измеримые или наблюдаемые характеристики системы.
• Параметры — числовые значения, которые определяют свойства или особенности моделируемой системы.
• Уравнения — математические соотношения, которые описывают зависимости между переменными и параметрами.
• Методы анализа — математические техники и инструменты, которые используются для исследования модели и получения результатов.
• Валидация — проверка корректности модели путем сравнения ее результатов с экспериментальными данными или другими надежными источниками.
• Прогнозирование — использование модели для предсказания поведения системы в условиях, которые не были исследованы экспериментально.
• Оптимизация — поиск оптимальных значений переменных или параметров модели с целью достижения наилучших результатов или решения задачи.

Математическое моделирование широко применяется во многих областях науки и техники, таких как физика, биология, экономика, социология и другие. Оно позволяет углубить понимание и развить теоретическую базу в этих областях, а также принимать обоснованные решения и предсказывать результаты в различных ситуациях.

Роль математического моделирования в науке и технике

Одной из основных задач математического моделирования является аппроксимация сложных систем и явлений с помощью математических уравнений и формул. Моделирование позволяет упростить сложные процессы, установить связи между различными факторами и предсказать результаты экспериментов или действий. Благодаря математическим моделям можно проводить виртуальные эксперименты, оптимизировать процессы, прогнозировать изменения и разрабатывать новые технологии и продукты.

Математическое моделирование также позволяет проводить исследования, которые могут быть невозможны или нежелательны с физической точки зрения. Например, моделирование позволяет изучать взаимодействия на молекулярном или атомном уровне, проводить эксперименты в опасных условиях или с большими объемами данных. Оно также позволяет быстро и эффективно проводить широкомасштабные исследования, оценивать различные варианты решений и прогнозировать их последствия.

Таким образом, математическое моделирование играет важную роль в развитии науки и техники, позволяя улучшать наши знания о мире, создавать новые технологии и продукты, а также принимать обоснованные решения в сложных ситуациях. Оно является мощным инструментом, который позволяет ученым и инженерам исследовать и понимать различные явления и процессы, а также предсказывать их поведение и эффекты.

Методы математического моделирования

Существует несколько основных методов математического моделирования, которые широко применяются в различных областях науки и техники:

1. Аналитическое моделирование. Этот метод основан на использовании математического аппарата для вывода аналитических формул, описывающих систему. Он позволяет получить точное решение математической модели, но требует высокой математической подготовки и может быть применен только в определенных случаях, когда система имеет простую структуру и известные законы.
2. Численное моделирование. Этот метод основан на использовании численных методов решения математических уравнений, таких как метод конечных разностей или метод конечных элементов. Он позволяет аппроксимировать решение системы с помощью дискретных значений и проводить вычисления на компьютере. Численное моделирование является более гибким и универсальным методом, который позволяет решать сложные системы, но требует больших вычислительных ресурсов.
3. Статистическое моделирование. Этот метод основан на использовании статистических методов и данных для построения модели системы и анализа её свойств. Он позволяет описать вероятностные закономерности в системе и проводить статистические выводы на основе имеющихся данных. Статистическое моделирование широко применяется в экономике, биологии, социологии и других областях, где данные о системе являются случайными.

Выбор метода математического моделирования зависит от характера системы, доступных данных, целей моделирования и ресурсов, которые можно выделить для проведения вычислений. В большинстве случаев используются комбинации различных методов для получения наиболее точных и адекватных результатов.

Аналитические методы

Основными аналитическими методами являются:

МетодОписание

Аналитическое решение дифференциального уравнения	Позволяет выразить решение дифференциального уравнения в явной форме с использованием математических операций.
Аналитическое решение системы линейных уравнений	Позволяет выразить решение системы линейных уравнений в явной форме с использованием методов линейной алгебры.
Аналитическое решение оптимизационной задачи	Позволяет выразить оптимальное решение задачи оптимизации в явной форме с использованием методов математического анализа.

Аналитические методы имеют ряд преимуществ, таких как возможность точного выражения зависимостей между переменными, высокая скорость выполнения и простота интерпретации результатов. Однако, они не всегда применимы для сложных задач, требующих численных методов или аппроксимации.

Численные методы

Численные методы позволяют найти приближенное решение, используя арифметические операции, итерационные процессы и аппроксимации. Они основаны на различных математических алгоритмах и аппроксимациях, которые позволяют получить результат с требуемой точностью.

Существует множество численных методов, включая методы решения уравнений, интерполяции и аппроксимации функций, численное интегрирование и дифференцирование, численное решение дифференциальных уравнений и многое другое.

Численные методы находят применение во многих областях науки и инженерии, таких как физика, экономика, биология, компьютерная графика и т.д. Они позволяют моделировать и анализировать сложные системы, расчеты которых невозможны или неэффективны с использованием аналитических методов.

Использование численных методов требует хорошего понимания математических основ и алгоритмов, а также умения программировать и работать с компьютером. Эти методы являются неотъемлемой частью современного математического моделирования и позволяют решать сложные задачи более эффективно и точно.

Применение математического моделирования

Одним из основных применений математического моделирования является нахождение оптимальных решений в сложных системах. Например, в экономике моделирование позволяет оптимизировать распределение ресурсов и прогнозировать результаты различных экономических политик. В физике математическое моделирование позволяет предсказывать движение тел, взаимодействие частиц и проводить эксперименты в виртуальной среде.

Математическое моделирование также широко применяется в медицине и биологии. На основе математических моделей и компьютерных симуляций ученые могут изучать динамику распространения заболеваний, разрабатывать новые лекарства и оптимизировать терапевтические стратегии. В экологии моделирование помогает прогнозировать влияние различных факторов на экосистемы и принимать меры по их сохранению и восстановлению.

Математическое моделирование также находит применение в социальных науках, позволяя изучать социальные процессы, такие как распространение информации, поведение людей и принятие решений в сложных ситуациях. Моделирование позволяет анализировать социальные сети, прогнозировать социальные тренды и разрабатывать стратегии социального воздействия.

Таким образом, математическое моделирование является неотъемлемой частью современной науки и техники. Оно позволяет ученым и инженерам получать новые знания, оптимизировать процессы и принимать обоснованные решения в сложных системах.

Математическое моделирование в физике

Математическое моделирование в физике проходит через три основных этапа: понятие, методы и применение.

На этапе понятия ученые определяют цель моделирования и формулируют основные понятия и законы физики, которые будут использоваться в модели. Это включает в себя выбор соответствующих математических уравнений и граничных условий.

На этапе методов ученые разрабатывают математические методы и алгоритмы, которые позволяют решать уравнения и проводить численные эксперименты. Это может включать методы численного интегрирования, методы конечных элементов и другие методы численного анализа.

На этапе применения ученые используют разработанные модели и методы для решения конкретных физических задач. Это может быть моделирование движения тела под воздействием силы тяжести, моделирование электромагнитных полей или моделирование распространения звука в среде.

Математическое моделирование в физике играет важную роль в научных исследованиях и разработке новых технологий. Оно позволяет ученым лучше понять физические явления, предсказывать их поведение и оптимизировать процессы. Благодаря математическому моделированию в физике мы можем создавать новые материалы, разрабатывать новые устройства и улучшать существующие технологии.

Математическое моделирование в экономике

Математическое моделирование играет важную роль в экономике, позволяя исследовать и предсказывать различные экономические процессы и явления. С помощью математических моделей экономисты могут анализировать взаимосвязи между различными экономическими переменными, прогнозировать будущие тенденции и оценивать эффективность различных политических и экономических мероприятий.

Одним из основных методов математического моделирования в экономике является построение эконометрических моделей. Эконометрическая модель представляет собой математическое описание взаимосвязей между экономическими переменными на основе статистических данных. С помощью таких моделей можно оценить влияние различных факторов на экономические показатели и провести анализ причинно-следственных связей.

Еще одним важным методом математического моделирования в экономике является оптимизационное моделирование. Оптимизационные модели позволяют находить оптимальные решения для различных экономических задач, таких как определение оптимального распределения ресурсов или планирование производства. С помощью таких моделей экономисты могут максимизировать прибыль, минимизировать затраты или достигать других целей в рамках ограничений и условий задачи.

Математическое моделирование также активно используется в финансовой экономике для прогнозирования цен на акции, определения рисков и разработки стратегий инвестирования. С помощью финансовых моделей можно анализировать динамику финансовых инструментов, оценивать и управлять рисками и принимать решения на основе математических моделей.

• Математическое моделирование позволяет исследовать и предсказывать экономические процессы.
• Эконометрические модели позволяют анализировать взаимосвязи между экономическими переменными.
• Оптимизационные модели помогают находить оптимальные решения для экономических задач.
• Финансовые модели используются для анализа динамики финансовых инструментов и разработки стратегий инвестирования.

Вопрос-ответ:

Какие этапы включает математическое моделирование?

Математическое моделирование включает три основных этапа: формулирование модели, решение модели и интерпретация результатов.

Что такое формулирование модели?

Формулирование модели — это процесс создания математического описания реальной системы или процесса, с использованием уравнений и других математических символов.

Какими методами можно решить математическую модель?

Для решения математической модели используются различные методы, включая аналитические методы, численные методы и методы компьютерного моделирования. Выбор метода зависит от сложности модели и доступных вычислительных ресурсов.

Какие результаты можно получить в результате математического моделирования?

Результаты математического моделирования могут быть различными, включая численные значения переменных модели, графики зависимостей, прогнозы и выводы о поведении системы или процесса.

В каких областях применяется математическое моделирование?

Математическое моделирование применяется во многих областях, включая физику, экономику, биологию, инженерию и социальные науки. Оно используется для изучения сложных систем, прогнозирования результатов экспериментов и оптимизации процессов.

Видео по теме: