Что такое троичная система счисления в математике 7 класс

Троичная система счисления в математике 7 класс. Узнайте, что это такое и как использовать троичную систему для записи чисел и решения математических задач.

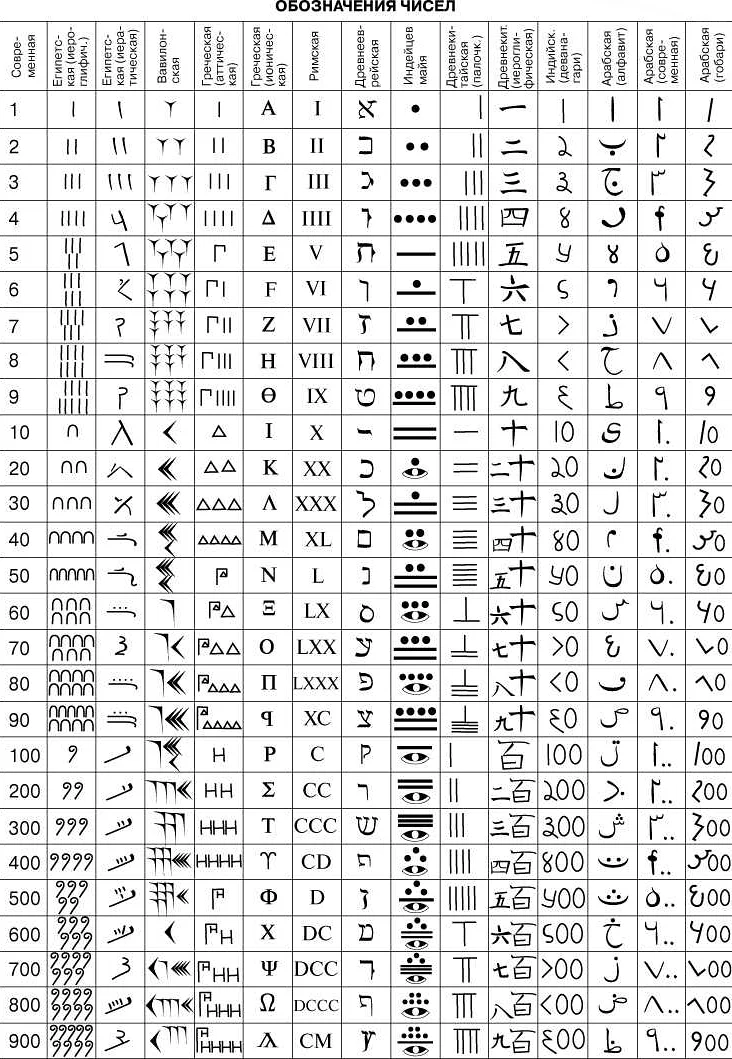
В математике одной из наиболее распространенных систем счисления является десятичная система, основанная на позиционном принципе. Однако, существуют и другие системы счисления, которые встречаются в различных областях науки и техники. Одной из таких систем является троичная система счисления.

Троичная система счисления, как и десятичная, основана на позиционном принципе. В ней используются три цифры: 0, 1 и 2. Это означает, что любое число можно представить в троичной системе, используя только эти три цифры.

При работе с троичной системой счисления необходимо учитывать основные правила. Одно из таких правил — умножение троичных чисел. Для этого нужно умножить старший разряд первого числа на второе число, затем умножить следующий разряд на второе число и так далее. После этого нужно сложить полученные произведения и записать результат.

Например, умножим числа 102 и 21 в троичной системе. В первом числе старший разряд равен 1, поэтому умножим его на 2. Получаем 2. Следующий разряд равен 0, поэтому его можно не учитывать. Младший разряд равен 2, поэтому его нужно умножить на 1. Получаем 2. Теперь сложим полученные произведения: 2 + 2 = 11. Таким образом, результат умножения чисел 102 и 21 в троичной системе равен 11.

Троичная система счисления может быть полезной в различных областях, например, в информационных технологиях при кодировании информации или при решении математических задач. Понимание основных понятий и правил троичной системы счисления поможет ученикам 7 класса развить свои навыки работы с числами и решать задачи более эффективно.

Что такое троичная система счисления?

В троичной системе счисления используется позиционное представление чисел, где каждая позиция представляет определенный разряд. Первая позиция представляет единицы, вторая — тройки, третья — девятки, четвертая — двадцатки и так далее. Значение числа определяется суммой произведений цифр на соответствующие степени тройки.

Троичная система счисления может использоваться для представления чисел в различных областях, таких как информатика, криптография, логика и других. Она также может быть полезна при решении математических задач и упрощении некоторых вычислений.

Видео по теме:

Зачем изучать троичную систему счисления?

Во-первых, изучение троичной системы счисления помогает развить логическое мышление и способность абстрактного мышления учащихся. Познавая новую систему счисления, дети учатся видеть закономерности и понимать, как могут быть представлены числа в другой системе.

Во-вторых, знание троичной системы счисления может быть полезным при изучении других областей науки, таких как информатика и электротехника. В этих областях троичная система счисления широко используется для представления данных и выполнения различных операций.

Наконец, изучение троичной системы счисления помогает учащимся более глубоко понять основы математики. В процессе изучения троичной системы счисления ученики сталкиваются с новыми понятиями, такими как разряды и позиционная система счисления, что помогает им лучше понять работу десятичной системы счисления.

В целом, изучение троичной системы счисления является важной частью математического образования, которая развивает способности учащихся и открывает новые возможности в изучении других областей науки.

Основные понятия

Троичное число – число, записанное в троичной системе счисления. Оно состоит из троичных разрядов, каждый из которых имеет свою степень числа 3.

Троичный разряд – позиция в троичном числе, которая определяет вес этого разряда. Первый разряд имеет вес 3^0 = 1, второй разряд – вес 3^1 = 3, третий разряд – вес 3^2 = 9 и т.д.

Троичное разложение – представление числа в виде суммы произведений троичных разрядов на их веса. Например, троичное число 102 в троичное разложение преобразуется как 1 * 3^2 + 0 * 3^1 + 2 * 3^0 = 9 + 0 + 2 = 11.

Троичная арифметика – операции сложения, вычитания, умножения и деления в троичной системе счисления. Основные правила троичной арифметики аналогичны правилам десятичной арифметики, но используются только цифры 0, 1 и 2.

Вопрос-ответ:

Для чего нужна троичная система счисления?

Троичная система счисления используется для представления чисел, использующих только три различных символа — 0, 1 и 2. Она может быть полезна при решении определенных задач, например, в информатике или в криптографии. Также она может помочь в понимании основных понятий и правил работы с системами счисления в целом.

Как перевести число из троичной системы счисления в десятичную?

Для перевода числа из троичной системы счисления в десятичную нужно умножить каждую цифру числа на соответствующую степень тройки и сложить полученные произведения. Например, число 201 в троичной системе счисления переводится в десятичную следующим образом: 2 * 3^2 + 0 * 3^1 + 1 * 3^0 = 18 + 0 + 1 = 19.

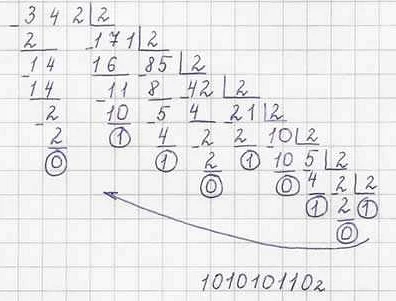
Как перевести число из десятичной системы счисления в троичную?

Для перевода числа из десятичной системы счисления в троичную нужно последовательно делить число на 3 и записывать остатки от деления в обратном порядке. Например, число 19 в десятичной системе счисления переводится в троичную следующим образом: 19 / 3 = 6 (остаток 1), 6 / 3 = 2 (остаток 0), 2 / 3 = 0 (остаток 2). Остатки записываются в обратном порядке, получаем число 201 в троичной системе счисления.

Как складывать и вычитать числа в троичной системе счисления?

Сложение и вычитание чисел в троичной системе счисления производится по тем же правилам, что и в десятичной системе счисления. При сложении чисел столбиком необходимо сложить соответствующие цифры чисел и, если сумма больше трех, запомнить единицу и прибавить ее к следующему разряду. При вычитании чисел столбиком необходимо вычесть соответствующие цифры чисел и, если разность меньше нуля, запомнить «заем» и добавить его к следующему разряду. Затем можно выполнять дополнительные операции, если это необходимо, и записать результат.

Цифры в троичной системе счисления

Цифра 0 в троичной системе счисления обозначает отсутствие единиц в данном разряде числа. Цифра 1 обозначает наличие одной единицы, а цифра 2 обозначает наличие двух единиц.

Например, число 10 в троичной системе счисления обозначает 1*3^1 + 0*3^0 = 3, а число 202 обозначает 2*3^2 + 0*3^1 + 2*3^0 = 18.

Цифры в троичной системе счисления используются для записи чисел, а также для выполнения арифметических операций, таких как сложение, вычитание, умножение и деление.

Основные правила использования цифр в троичной системе счисления:

• Максимальная цифра — 2, поэтому цифры больше 2 не используются.
• Следующее число после 2 — 10, где 1 обозначает 1*3 и 0 обозначает 0 единиц.
• Аналогично десятичной системе счисления, в троичной системе счисления число 10 обозначает 1*3^1 + 0*3^0 = 3.

Троичная система счисления может быть использована в различных областях, таких как компьютерные науки, криптография и теория информации. Например, в компьютерных системах троичная система счисления может использоваться для представления данных в виде триад (наборов из трех битов) или для уменьшения количества проводов при передаче информации.

Разряды в троичной системе счисления

Троичная система счисления основана на использовании трех цифр: 0, 1 и 2. В ней каждая цифра имеет свой разряд, который определяет ее весовое значение.

Первый разряд в троичной системе называется единицами. В нем записываются все цифры, которые не имеют разряда. Например, число 102 в троичной системе будет представлено как 002, где 2 — цифра в разряде единиц.

Второй разряд в троичной системе называется тройками. В нем записываются все цифры, которые имеют весовое значение, равное степени тройки. Например, число 102 в троичной системе будет представлено как 010, где 1 — цифра в разряде троек.

Третий разряд в троичной системе называется девятками. В нем записываются все цифры, которые имеют весовое значение, равное степени тройки второй степени. Например, число 102 в троичной системе будет представлено как 100, где 1 — цифра в разряде девяток.

Таким образом, каждый разряд в троичной системе счисления определяет весовое значение цифры, записанной в нем, и влияет на общее значение числа.

Правила

В троичной системе счисления используются три цифры: 0, 1 и 2. Чтобы записать числа, мы используем соответствующие цифры в разрядах чисел. Каждая цифра в разряде имеет определенный вес:

• 0 — вес 0
• 1 — вес 1
• 2 — вес 2

Для записи чисел в троичной системе счисления применяются следующие правила:

1. Порядок следования цифр: Цифры записываются последовательно, начиная с самого младшего разряда (справа налево).

2. Переход к следующему разряду: Когда число достигает своего максимального значения в данном разряде, следующая цифра увеличивается на 1, а текущая цифра становится равной 0.

3. Вычитание: Когда требуется выполнить вычитание, необходимо занимать 1 из следующего разряда. Если следующий разряд равен 0, то нужно занять 2 из разряда, стоящего за ним.

4. Дополнение: Чтобы записать отрицательное число в троичной системе счисления, необходимо сначала записать его положительное значение, а затем изменить знаки всех цифр (0 на 2, 1 на 1 и 2 на 0), а также добавить 1 к полученному числу.

Соблюдение этих правил позволяет корректно записывать и выполнять операции с числами в троичной системе счисления.

Как записывать числа в троичной системе счисления?

Троичная система счисления основана на том, что в числах можно использовать только три символа: 0, 1 и 2. Это отличается от десятичной системы счисления, где используются десять символов (от 0 до 9).

Для записи чисел в троичной системе счисления используется аналогичный принцип, как и в десятичной системе. Каждая позиция числа имеет свой вес, который определяется степенью числа 3. Первая позиция считается справа и имеет вес 3^0 (равен 1), вторая позиция имеет вес 3^1 (равен 3), третья позиция имеет вес 3^2 (равен 9) и так далее.

Например, число 201 в троичной системе счисления можно разложить следующим образом:

Позиция3^23^13^0

Значение

2

0

1

Чтобы записать число 201 в троичной системе, нужно умножить каждую цифру числа на соответствующий вес и сложить полученные произведения. В данном случае это будет: (2 * 3^2) + (0 * 3^1) + (1 * 3^0) = 18 + 0 + 1 = 19.

Таким образом, число 201 в троичной системе счисления записывается как 19.

Как складывать числа в троичной системе счисления?

Для сложения чисел в троичной системе счисления следует придерживаться следующих правил:

1. Сложение выполняется поколоночно, начиная справа, как в десятичной системе.

2. Если сумма цифр в одной позиции равна 0 или 1, результат заносится в соответствующую позицию суммы.

3. Если сумма цифр в одной позиции равна 2, результат заносится в соответствующую позицию суммы, а 1 переносится на следующую позицию слева.

4. Если после выполнения сложения в самой левой позиции возникает перенос, он также учитывается.

Пример:

Сложить числа 101 и 110 в троичной системе счисления.

1 0 1

+ 1 1 0

________

1 0 1 1

Таким образом, сумма чисел 101 и 110 в троичной системе счисления равна 1011.

Как вычитать числа в троичной системе счисления?

Для вычитания чисел в троичной системе счисления необходимо следовать определенным правилам. В троичной системе используются всего три цифры: 0, 1 и 2. Для выполнения вычитания, необходимо вычитаемое записать под уменьшаемым так, чтобы цифры стояли друг под другом.

Правила вычитания чисел в троичной системе счисления:

1. Если цифра уменьшаемого больше цифры вычитаемого, то разность записывается прямо под уменьшаемым.
2. Если цифра уменьшаемого меньше цифры вычитаемого, то необходимо занять единицу из следующего разряда и уменьшить эту единицу на единицу в текущем разряде.
3. Если цифра уменьшаемого равна цифре вычитаемого, то разность равна нулю и записывается прямо под уменьшаемым.

Пример:

• Вычитание числа 102 из числа 210:
  2

  1

  0

  —  1

  ————

  10

  ————

  Результат вычитания: 10 (в троичной системе счисления)

Используя эти правила, можно выполнять вычитание чисел в троичной системе счисления. Важно помнить, что результат вычитания также будет представлен в троичной системе счисления.

Как умножать числа в троичной системе счисления?

Умножение чисел в троичной системе счисления осуществляется по аналогии с умножением чисел в десятичной системе счисления. Для этого необходимо выполнить следующие шаги:

1. Разместите первое число (множимое) в верхней строке и второе число (множитель) под ним.
2. Умножайте каждую цифру во втором числе на каждую цифру в первом числе, начиная справа.
3. Запишите результаты промежуточных умножений в столбцы, начиная справа.
4. Просуммируйте результаты промежуточных умножений для получения итогового произведения.

Приведем пример умножения числа 213 на число 123:

		2	1
	×	1	2
		2	1
+	2	1

В данном примере результат умножения равен 2213.

Таким образом, умножение чисел в троичной системе счисления осуществляется путем умножения каждой цифры одного числа на каждую цифру другого числа и последующего сложения результатов.