Что значит величина угла в математике

Угол в математике — это мера поворота между двумя лучами, указывающими на область пространства. Величина угла измеряется в градусах или радианах и используется для определения геометрических форм, а также в различных научных и инженерных областях. Углы имеют важное значение в тригонометрии и геометрии, а также в алгебре и физике. Понимание величины угла помогает анализировать и решать различные математические задачи и проблемы.

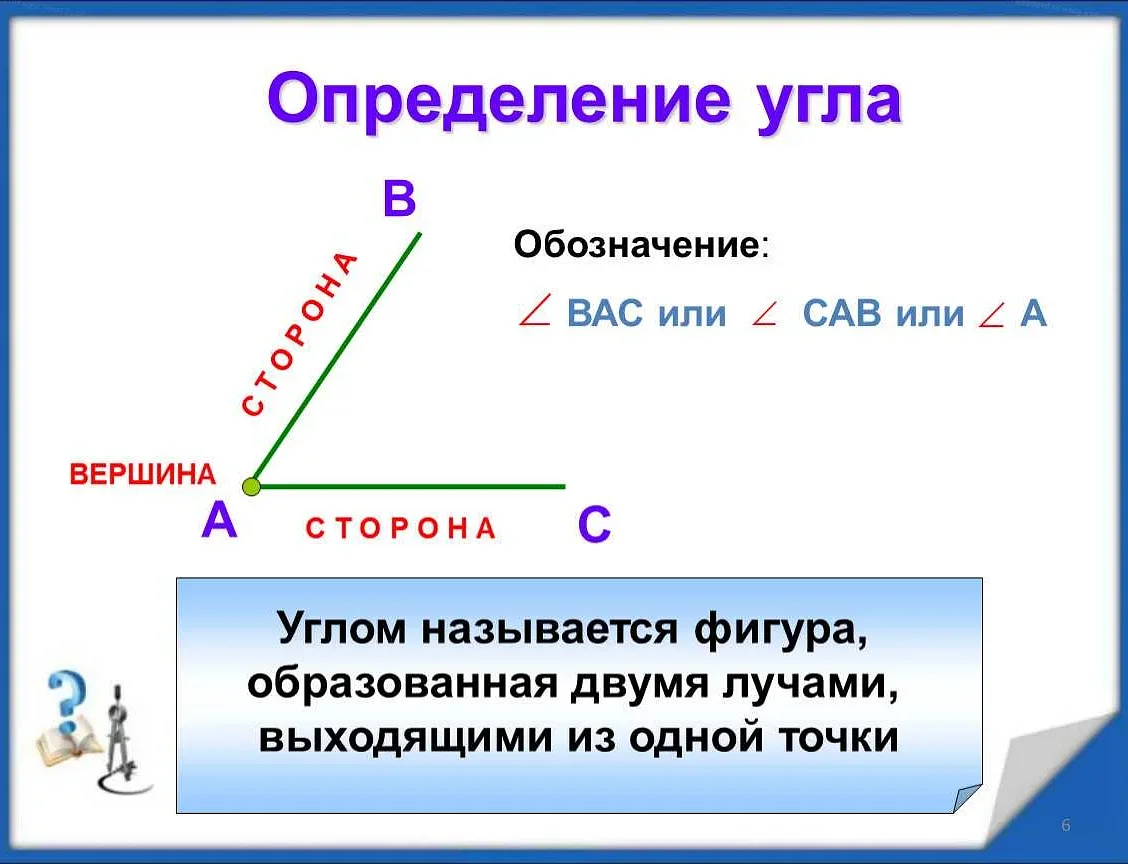
Угол — одна из основных геометрических фигур, широко используемая в математике. Это фигура, образованная двумя лучами, исходящими из одной точки, называемой вершиной угла. Угол измеряется в градусах, минутах и секундах, и его значение определяется мерой поворота одного из лучей вокруг вершины.

Значение угла имеет большое значение в математике и его применение находится в разных областях науки и техники. Например, в геометрии углы используются для измерения форм и размеров фигур, а также для решения задач по построению. В физике углы играют важную роль при расчетах траекторий и скоростей движения тел. А в астрономии углы позволяют определить положение небесных тел и предсказать их движение.

Знание понятия угла и умение работать с ним являются важными навыками для различных профессий, связанных с точными науками. Например, инженеры, архитекторы, пилоты и навигаторы регулярно сталкиваются с задачами, требующими измерения и расчета углов. Они используют специальные инструменты, такие как гониометр, для точного измерения углов и выполнения необходимых расчетов.

В заключение, понятие угла имеет большое значение в математике и его применение широко распространено в различных областях науки и техники. Знание углов и умение работать с ними является неотъемлемой частью математической грамотности и может быть полезно в повседневной жизни и профессиональной деятельности.

Угол в математике: определение и свойства

Основные характеристики угла включают его меру и тип. Мера угла измеряется в градусах, минутах и секундах, причем полный угол составляет 360 градусов. Тип угла зависит от его меры и может быть остроугольным (меньше 90 градусов), прямым (равен 90 градусам), тупоугольным (больше 90 градусов) или полным (равен 360 градусам).

Углы могут быть также смежными, вертикальными, суплементарными и комлементарными. Смежные углы — это два угла, которые имеют общую сторону и вершину. Вертикальные углы — это пара углов, которые находятся на противоположных сторонах пересекающихся прямых и равны между собой. Суплементарные углы — это два угла, сумма которых равна 180 градусов. Комлементарные углы — это два угла, сумма которых равна 90 градусов.

Углы в математике играют важную роль при решении геометрических задач, а также в других областях, таких как физика, инженерия и архитектура. Понимание определения угла и его свойств поможет в анализе и решении различных математических проблем.

Видео по теме:

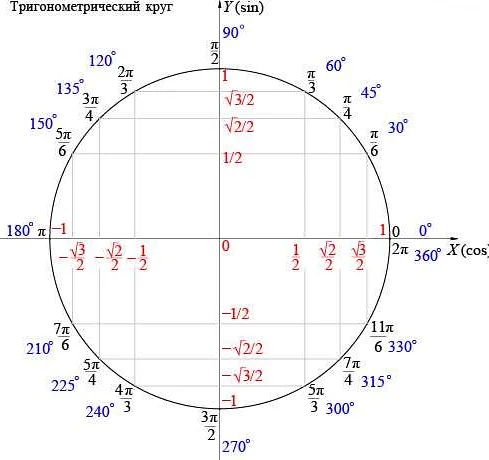
Меры углов: радианы, градусы и грады

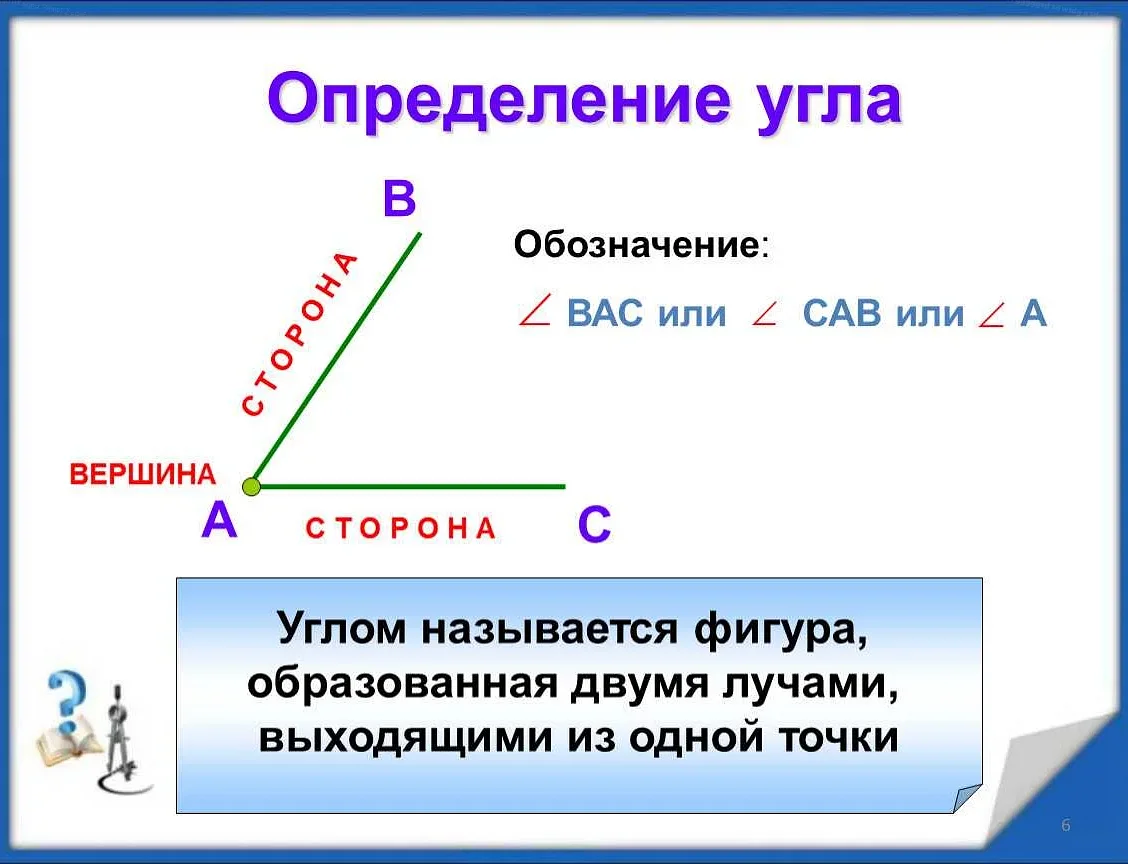
Наиболее распространенными мерами углов являются радианы, градусы и грады.

Радиан – это единица измерения угла, которая основана на соотношении длины дуги окружности к радиусу этой окружности. В радианах угол измеряется как отношение длины дуги к радиусу.

Градус – это единица измерения угла, которая основана на делении окружности на 360 равных частей. Градус обозначается символом °.

Град – это единица измерения угла, которая основана на делении окружности на 400 равных частей. Град обозначается символом г.

Часто в математических расчетах используется градусная мера углов, однако в некоторых областях науки и инженерии применяются радианы или грады.

Радианы обычно используются в тригонометрии и анализе, поскольку имеют простую связь с длиной дуги окружности. Грады в основном используются в геодезии и навигации, так как деление окружности на 400 частей позволяет более точно измерять углы направления.

Зная соотношение между разными единицами измерения углов, можно производить преобразования между ними.

Например, 180 градусов равны π радианам и 200 градам, так как 180° = π рад = 200 г.

Таким образом, понимание мер углов – важный аспект математики, который находит применение в различных областях науки и техники.

Различные типы углов: острые, прямые, тупые и рефлексные

• Острый угол — это угол, чья величина меньше 90 градусов. Он размещается между двумя лучами, которые сходятся внутри круга.
• Прямой угол — это угол, равный 90 градусам. Он образуется двумя перпендикулярными лучами и напоминает букву «L».
• Тупой угол — это угол, чья величина больше 90 градусов, но меньше 180 градусов. Такой угол размещается между двумя лучами, которые сходятся внутри круга, и его открытая сторона направлена внутрь круга.
• Рефлексный угол — это угол, чья величина больше 180 градусов, но меньше 360 градусов. Он образуется двумя лучами, которые сходятся внутри круга, и его открытая сторона направлена наружу круга.

Знание различных типов углов важно для изучения геометрии и решения задач, связанных с измерением и сравнением углов. Понимание этих типов углов помогает определить их свойства и использовать их в различных математических вычислениях.

Вопрос-ответ:

Какое значение имеет угол в математике?

Угол в математике является понятием, определяющим отношение между двумя линиями или плоскостями. Он измеряется в градусах и используется для описания поворота, наклона и ориентации объектов.

Какое значение имеет угол в геометрии?

В геометрии угол используется для измерения отклонения или поворота между двумя линиями или плоскостями. Он позволяет определить геометрические свойства фигур, такие как треугольники, прямоугольники и круги, и решать различные задачи связанные с конструкцией и измерением.

Какую роль играют углы в тригонометрии?

Углы играют важную роль в тригонометрии, которая изучает связи между углами и сторонами треугольника. Тригонометрические функции, такие как синус, косинус и тангенс, используются для вычисления значений углов и сторон треугольников и применяются в различных областях науки и техники.

Каким образом углы используются в физике?

В физике углы используются для описания направления и ориентации объектов, а также для измерения вращения и векторных величин. Например, угол может быть использован для определения направления силы, момента силы, скорости или вектора смещения. Углы также играют важную роль в оптике, механике и электромагнетизме.

Углы в геометрии: треугольники и многоугольники

В геометрии угол представляет собой фигуру, образованную двумя лучами, которые имеют общую точку начала, называемую вершиной угла. Углы могут быть различных типов и классифицируются по их величине.

В треугольниках и многоугольниках углы играют важную роль. В треугольнике каждый угол может быть описан с помощью трех точек вершин и каждый угол имеет свою меру. Сумма углов в треугольнике всегда равна 180 градусов.

В многоугольниках, углы между сторонами также имеют свои меры и сумма всех углов зависит от количества сторон фигуры. Например, в четырехугольнике сумма углов равна 360 градусов, в пятиугольнике — 540 градусов и так далее.

Знание углов в геометрии позволяет решать различные задачи, связанные с построением и измерением фигур. Например, зная величину одного угла треугольника, можно найти меры остальных углов. Также углы помогают определить форму многоугольника и классифицировать его.

Вся геометрия тесно связана с понятием угла и его измерениями. Поэтому понимание углов в геометрии является необходимым для успешного решения задач и построения фигур.

Тригонометрические функции углов

Тригонометрические функции углов определяются с помощью отношений между сторонами прямоугольного треугольника. Основными тригонометрическими функциями углов являются синус, косинус и тангенс.

Синус угла определяется как отношение противолежащего катета к гипотенузе треугольника. Он обозначается символом sin.

Косинус угла определяется как отношение прилежащего катета к гипотенузе треугольника. Он обозначается символом cos.

Тангенс угла определяется как отношение противолежащего катета к прилежащему катету треугольника. Он обозначается символом tan.

Тригонометрические функции углов имеют множество свойств и связей между собой. Они используются для расчета различных параметров и решения задач в геометрии, физике, инженерии, астрономии и других областях науки и техники.

Важно отметить, что тригонометрические функции углов имеют периодические свойства и принимают значения в пределах от -1 до 1. Это связано с тем, что синус, косинус и тангенс угла зависят от соотношений между сторонами треугольника и углом.

Изучение тригонометрических функций углов помогает понять и описать различные явления и процессы в природе и в научных исследованиях. Они являются неотъемлемой частью математического аппарата и находят широкое применение в различных областях знания.

Углы в физике: векторы и силы

В физике углы играют важную роль при рассмотрении векторов и сил. Угол между двумя векторами определяет направление и силу взаимодействия между ними.

Угол между двумя векторами можно вычислить с помощью скалярного произведения векторов. Зная значения координат векторов, можно определить косинус угла между ними и выразить его через скалярное произведение. Это позволяет установить величину и направление силы взаимодействия между векторами.

Углы также используются при анализе сил. При рассмотрении системы сил, углы между силами позволяют определить, как они будут взаимодействовать между собой. Угол между силами может определять их суммарную силу и направление движения тела под действием этих сил.

В физике углы также используются для определения момента силы. Момент силы зависит от величины силы и ее расположения относительно точки вращения. При анализе системы сил, углы между силами и точкой вращения позволяют определить момент силы и его влияние на вращение тела.

Применение углов в инженерии и архитектуре

В инженерии углы используются для определения направления и наклона строительных элементов, таких как стены, столбы и балки. Кроме того, углы помогают инженерам разрабатывать эффективные и безопасные маршруты для дорог и железных дорог, а также для планирования размещения городской инфраструктуры.

В архитектуре углы используются для создания эстетических и симметричных форм зданий. Архитекторы используют углы для определения геометрической структуры и пропорций здания, а также для создания привлекательных фасадов и интерьеров.

Кроме того, углы используются в измерениях и планировании. Инженеры и архитекторы часто используют инструменты, такие как геодезические инструменты и компьютерные программы, чтобы измерить углы и создавать точные планы и чертежи.

В целом, понимание и применение углов является неотъемлемой частью работы инженеров и архитекторов, помогая им создавать безопасные, эффективные и привлекательные конструкции и здания.

Роль углов в информационных технологиях

В компьютерной графике углы используются для определения направления объектов, их вращения и ориентации. Знание углов позволяет создавать трехмерные модели, анимацию и спецэффекты. Например, при разработке компьютерных игр углы используются для определения движения персонажей и объектов, а также для создания эффектов освещения и теней.

В информационных технологиях углы также имеют прямое применение в обработке изображений и видео. Например, при сжатии изображений используется алгоритм дискретного косинусного преобразования (DCT), который основывается на представлении изображения в виде суммы синусоидальных функций с различными углами. Углы позволяют представить информацию о частотах изменения яркости пикселей и эффективно сжать изображение без существенной потери качества.

Кроме того, углы используются в криптографии, где они играют важную роль в алгоритмах шифрования и проверки целостности данных. Углы могут использоваться для генерации случайных чисел и создания криптографических ключей.

Таким образом, углы являются неотъемлемой частью информационных технологий и играют важную роль в обработке данных, компьютерной графике и криптографии.