Что такое вероятность в математике

Вероятность в математике – это числовая характеристика, отражающая степень возможности наступления события. Она позволяет оценить, насколько вероятно наступление того или иного исхода в эксперименте или случайном событии. Вероятность выражается числом от 0 до 1, где 0 означает невозможность, а 1 – полную достоверность наступления события.

Вероятность — это понятие, широко используемое в математике, позволяющее оценить степень возможности наступления какого-либо события. Она играет важную роль во многих областях науки, таких как статистика, теория игр, физика и другие. Вероятность является одной из основных концепций вероятностного исчисления и позволяет предсказать возможные исходы различных ситуаций.

Основные принципы вероятности:

1. Принцип суммы вероятностей — вероятность наступления одного из несовместных событий равна сумме их вероятностей. Например, вероятность выпадения герба или решки при подбрасывании монеты равна 1.
2. Принцип умножения вероятностей — вероятность наступления нескольких независимых событий равна произведению их вероятностей. Например, вероятность выпадения герба при подбрасывании двух монет равна 0.5 * 0.5 = 0.25.
3. Принцип дополнения — вероятность наступления события A равна единице минус вероятность наступления противоположного ему события. Например, вероятность получить орла при подбрасывании монеты равна 1 — вероятность получить решку.

Примеры применения вероятности:

1. Вероятность выигрыша в лотерее.

2. Вероятность выпадения нужной карты в колоде.

3. Вероятность попадания в цель при стрельбе.

4. Вероятность наступления определенного заболевания.

Изучение и применение вероятности позволяет более точно предсказывать и оценивать различные события, что является важным инструментом в решении реальных задач и принятии решений.

Что такое вероятность в математике

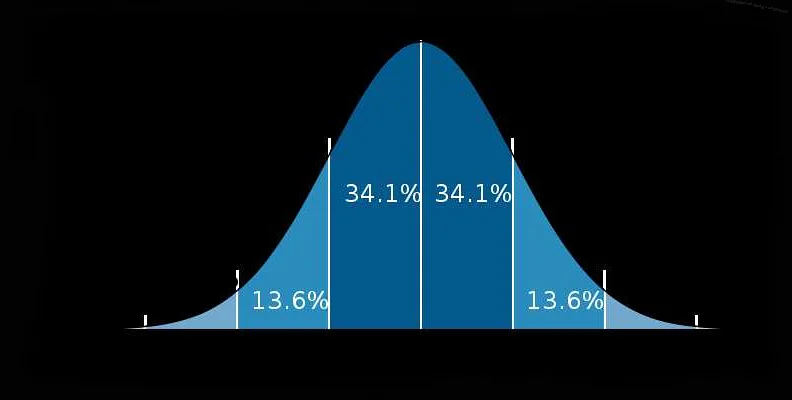
Вероятность измеряется числом от 0 до 1, где 0 означает полную невозможность наступления события, а 1 – абсолютную уверенность в его наступлении. Промежуточные значения указывают на степень возможности события.

Например:

Если подбросить правильную монету, то вероятность выпадения орла равна 0,5, так как вероятность выпадения орла и решки одинакова.

Вероятность может быть вычислена с помощью математических формул и методов. Для этого используются теория вероятностей и статистика. Они помогают предсказать, какие события могут произойти в определенных условиях.

Важно отметить, что вероятность – это не гарантия наступления или ненаступления события. Она лишь оценивает, насколько вероятно это событие.

Вероятность имеет множество применений в реальной жизни, таких как прогноз погоды, экономические прогнозы, шансы в играх и многое другое. Понимание и использование вероятности позволяет принимать более осознанные решения и делать предсказания.

Видео по теме:

Основные принципы вероятности

Основные принципы вероятности включают:

1. Принцип равной вероятности	События, которые имеют одинаковые возможности наступления, считаются равновероятными. Например, при подбрасывании честной монеты, вероятность выпадения орла или решки равна 0.5.
2. Принцип суммы вероятностей	Сумма вероятностей всех возможных исходов события равна 1. Например, если при подбрасывании монеты есть только два возможных исхода — орел и решка, то вероятность выпадения орла и решки в сумме равна 1.
3. Принцип умножения вероятностей	Вероятность наступления двух независимых событий, происходящих одновременно, равна произведению их вероятностей. Например, вероятность выпадения орла и решки при двух подбрасываниях монеты будет равна 0.5 * 0.5 = 0.25.

Эти основные принципы вероятности являются основой для дальнейших вычислений и применений теории вероятностей.

Классическое определение вероятности

Пусть имеется некоторый испытательный эксперимент, который может иметь N различных исходов. Если каждый исход эксперимента имеет равную вероятность произойти, то вероятность события A, которое может произойти в результате этого эксперимента, определяется следующим образом:

P(A) = (число исходов, благоприятствующих событию A) / (общее число возможных исходов эксперимента)

Таким образом, вероятность события A – это отношение числа исходов, благоприятствующих событию A, к общему числу исходов эксперимента.

Классическое определение вероятности подходит для экспериментов, в которых все исходы равновероятны. Оно применим, например, к бросанию обычной игральной кости или выбору карты из колоды без возвращения. Однако, в реальных ситуациях часто возникают эксперименты, в которых исходы не равновероятны. В таких случаях применяются другие определения вероятности, такие как статистическое или субъективное определение.

Статистическое определение вероятности

Статистическое определение вероятности основано на идеи проведения серии экспериментов и подсчете относительной частоты наступления события. Вероятность события определяется как отношение числа благоприятных исходов (наступления события) к общему числу возможных исходов.

Для проведения статистического определения вероятности необходимо иметь достаточно большое количество наблюдений. Чем больше экспериментов проведено, тем более точным будет определение вероятности.

Примером статистического определения вероятности может служить подсчет вероятности выпадения определенной стороны монеты. Для этого необходимо провести серию бросков монеты и подсчитать, как часто она выпадает на ту или иную сторону. Вероятность выпадения одной стороны монеты будет равна отношению числа выпадений этой стороны к общему числу бросков.

Статистическое определение вероятности широко применяется в различных областях, включая экономику, медицину, социологию и другие. Оно позволяет оценивать вероятность наступления событий на основе наблюдений и анализа статистических данных.

Аксиоматическое определение вероятности

Согласно аксиоматическому определению, вероятность — это числовая мера, которая присваивается событиям и удовлетворяет определенным аксиомам.

Основные аксиомы аксиоматического определения вероятности:

1. Вероятность события всегда неотрицательна и не превышает единицу: 0 ≤ P(A) ≤ 1.
2. Вероятность достоверного события равна единице: P(S) = 1, где S — пространство элементарных исходов.
3. Если события A и B несовместны (не могут произойти одновременно), то вероятность их объединения равна сумме вероятностей каждого из них: P(A ∪ B) = P(A) + P(B).

Аксиоматическое определение вероятности позволяет строить математическую модель для анализа случайных событий и предсказания их возможных исходов. Это позволяет решать множество задач в таких областях, как статистика, теория игр, финансы и другие.

Примеры применения вероятности в реальной жизни

ПримерОписание

1	Прогнозирование погоды
2	Оценка риска в страховании
3	Разработка стратегии в играх
4	Оценка эффективности медицинских тестов
5	Построение финансовых моделей

Прогнозирование погоды — одно из самых популярных применений вероятности в реальной жизни. С использованием статистических данных и моделей, вероятность того, что определенные погодные условия будут иметь место, может быть предсказана с определенной степенью точности. Это позволяет людям принимать соответствующие меры, например, взять зонт с собой или запланировать пикник в зависимости от ожидаемой погоды.

В страховании вероятность также играет важную роль. Страховые компании используют вероятность для оценки риска и определения страховых премий. Например, при страховании автомобиля, вероятность дорожно-транспортного происшествия может быть учтена при расчете стоимости страховки.

Вероятность также может быть полезна при разработке стратегии в играх. Например, в шахматах игроки могут использовать вероятность для прогнозирования возможных ходов и выбора наиболее оптимального варианта. Вероятность также может быть применена в карточных играх и азартных играх для оценки шансов на выигрыш.

В медицине вероятность используется для оценки эффективности медицинских тестов. Например, вероятность того, что тест на определенное заболевание даст правильный результат, может быть определена с использованием статистических методов. Это позволяет врачам принимать информированные решения и рекомендации по лечению.

Наконец, вероятность играет важную роль в построении финансовых моделей. Финансовые аналитики используют вероятность для моделирования рыночных условий и прогнозирования изменений цен на акции, валюты и другие финансовые инструменты. Это помогает инвесторам принимать решения о своих инвестициях на основе ожидаемых доходов и рисков.

Это лишь некоторые примеры применения вероятности в реальной жизни. Вероятность используется во многих других областях, включая логистику, транспорт, экологию и многое другое. Понимание и применение вероятности позволяет нам лучше понять и предсказать различные события и принимать обоснованные решения.

Математические модели и вероятность

Математическая модель — это упрощенное представление реального мира, которое позволяет анализировать и изучать различные явления. Математические модели позволяют формализовать ситуации и процессы, выделить основные факторы и переменные, исследовать различные варианты развития событий.

Вероятность в математических моделях вычисляется с использованием базовых принципов вероятности, таких как принцип равномерного распределения, принцип суммы, принцип произведения и другие.

Примером математической модели, в которой используется вероятность, может быть модель случайного блуждания. В этой модели предполагается, что объект может двигаться случайно в разных направлениях с определенными вероятностями. Используя вероятность, можно предсказать, сколько времени объект проведет в определенных точках или как долго ему потребуется, чтобы достичь определенной цели.

Математические модели и вероятность широко применяются в различных областях науки и техники. Они используются в физике, экономике, социологии, биологии и других дисциплинах для анализа и прогнозирования различных явлений и процессов. Использование математических моделей и вероятности позволяет сделать более точные прогнозы, принять обоснованные решения и оптимизировать различные системы и процессы.

Вопрос-ответ:

Что такое вероятность в математике?

Вероятность в математике — это числовая характеристика, показывающая, насколько вероятно наступление определенного события. Она измеряется от 0 до 1, где 0 означает невозможность события, а 1 — его полную достоверность.

Какие основные принципы вероятности существуют?

Основные принципы вероятности включают в себя: принцип сложения, принцип умножения и принцип дополнения. Принцип сложения гласит, что вероятность наступления хотя бы одного из несовместных событий равна сумме их вероятностей. Принцип умножения утверждает, что вероятность наступления двух независимых событий равна произведению их вероятностей. Принцип дополнения говорит о том, что вероятность наступления события, дополняющего некоторое другое событие до полной группы, равна единице минус вероятность первого события.

Какие примеры можно привести для объяснения вероятности?

Примерами для объяснения вероятности могут служить игра в кости или подбрасывание монеты. Например, при подбрасывании честной монеты вероятность выпадения орла равна 0,5, а вероятность выпадения решки также равна 0,5. В игре в кости вероятность выпадения любого из шести чисел равна 1/6.

Как вероятность связана с математической статистикой?

Вероятность и математическая статистика тесно связаны между собой. Вероятность является одним из основных понятий математической статистики и используется для описания случайных явлений и событий. Она позволяет оценить вероятность наступления определенного события и применяется для построения статистических моделей и выводов на основе наблюдений и экспериментов.