Когда проходят матрицу в математике
Содержимое
- 1 Когда проходят матрицу в математике
- 1.1 Определение матрицы в математике
- 1.2 Важность решения матрицы в практических задачах
- 1.3 Факторы, влияющие на время решения матрицы
- 1.4 Сложность матрицы и время решения
- 1.5 Влияние размерности матрицы на время решения
- 1.6 Методы решения матрицы и их влияние на время
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Какое время обычно занимает решение матрицы в математике?
- 1.8.0.2 Есть ли способы ускорить процесс решения матрицы?
- 1.8.0.3 Как влияет размер матрицы на время ее решения?
- 1.8.0.4 Можно ли сократить время решения матрицы, используя компьютер?
- 1.8.0.5 Какие еще факторы могут влиять на время решения матрицы?
- 1.9 Применение компьютерных программ для решения матрицы
- 1.10 Советы по оптимизации времени решения матрицы
Матрица в математике применяется для решения систем линейных уравнений и различных операций над векторами. Узнайте, когда и как изучают и проходят матрицу в школьной и высшей математике.
Матрицы — это важная часть математики, которая находит применение во многих областях, включая физику, экономику и компьютерные науки. Однако, решение сложных матричных задач может занять много времени, особенно если матрица имеет большой размер или используется сложный алгоритм решения.
Определить время прохождения матрицы в математике можно с помощью анализа алгоритма решения. Некоторые алгоритмы имеют сложность O(n^3), где n — размер матрицы. Это означает, что время решения задачи увеличивается в кубической зависимости от размера матрицы. Таким образом, чем больше размер матрицы, тем дольше будет занимать решение.
Например, решение системы линейных уравнений с использованием метода Гаусса-Жордана требует приведения матрицы к ступенчатому виду, что требует O(n^3) операций. Таким образом, для матрицы размером 100×100 понадобится около 1 миллиона операций, а для матрицы 1000×1000 — уже 1 миллиард операций.
Существуют также алгоритмы с более эффективной сложностью, например, алгоритм Штрассена, который позволяет умножать матрицы за время O(n^log2(7)). Однако, такие алгоритмы требуют более сложной реализации и не всегда оправдывают свою эффективность.
Таким образом, время прохождения матрицы в математике зависит от размера матрицы и выбранного алгоритма решения. Если вам необходимо решить задачу, связанную с матрицами, важно учитывать время, которое может потребоваться на решение, особенно если матрица имеет большой размер или используется сложный алгоритм.
Определение матрицы в математике
Обычно элементы матрицы обозначаются символами и располагаются в виде прямоугольной таблицы, где каждое число находится в определенной ячейке. Например, матрица размером 2×3 будет иметь 2 строки и 3 столбца.
Матрицы широко используются в различных областях математики и ее приложений. Они играют важную роль в линейной алгебре, теории вероятности, теории графов, компьютерной графике и других дисциплинах. Матрицы также являются основой для решения систем линейных уравнений и для проведения линейных преобразований.
Матрицы могут быть различных типов, например, квадратные, прямоугольные, диагональные, верхнетреугольные, нижнетреугольные и др. Каждый тип матрицы имеет свои особенности и свойства, которые определяются расположением и значениями ее элементов.
Определение матрицы является важным шагом в изучении и понимании ее свойств и применений. Понимание основных понятий и терминов, связанных с матрицами, позволяет эффективно работать с ними и использовать их для решения различных задач.
Важность решения матрицы в практических задачах
Одной из важных областей, где матрицы играют ключевую роль, является компьютерная графика. В компьютерной графике матрицы используются для преобразования объектов, а также для определения их положения, ориентации и размеров. Например, матрицы трансформации позволяют перемещать, масштабировать и вращать графические объекты на экране.
Матрицы также широко применяются в статистике и экономике. В статистике, матрицы используются для обработки и анализа данных, решения систем уравнений и построения прогнозов. В экономике, матрицы используются для моделирования экономических процессов, анализа международной торговли и определения равновесия в экономике.
Область примененияПримеры задач
| Физика | Матрицы используются для моделирования физических систем, решения уравнений движения и определения сил и энергии. |
| Инженерия | Матрицы применяются для решения задач в области электротехники, механики, строительства и других инженерных дисциплин. |
| Криптография | Матрицы используются для шифрования и дешифрования сообщений, а также для обеспечения безопасности информации. |
Таким образом, решение матрицы является неотъемлемой частью решения множества практических задач. Умение работать с матрицами и применять их в различных областях науки и техники является важным навыком для специалистов во многих областях деятельности.
Факторы, влияющие на время решения матрицы
Время, затрачиваемое на решение матрицы в математике, зависит от нескольких факторов. Ниже перечислены основные из них:
- Размер матрицы: Чем больше размер матрицы, тем больше вычислений требуется для её решения, и, следовательно, тем больше времени потребуется.
- Структура матрицы: Некоторые структуры матрицы могут обладать свойствами, которые позволяют снизить время решения. Например, если матрица является разреженной, то есть содержит много нулевых элементов, то можно использовать специальные алгоритмы для оптимизации вычислений.
- Выбор метода решения: Существует несколько методов решения матрицы, таких как метод Гаусса, метод Якоби и метод простых итераций. Каждый из них имеет свои особенности и может потребовать разное количество времени для решения.
- Аппаратное обеспечение: Компьютер, на котором происходит решение матрицы, также оказывает влияние на время выполнения. Более мощное аппаратное обеспечение может обрабатывать вычисления быстрее и, следовательно, сокращать время решения.
Учитывая данные факторы, можно оптимизировать процесс решения матрицы и сократить время, затрачиваемое на вычисления.
Сложность матрицы и время решения
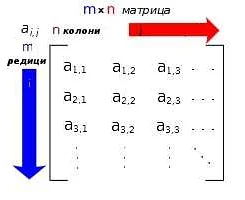
Размер матрицы определяется количеством строк и столбцов. Чем больше размер матрицы, тем сложнее ее решение. Использование больших матриц может привести к значительному увеличению времени, необходимого для выполнения вычислений.
Структура матрицы также влияет на ее сложность. Некоторые матрицы имеют специальные свойства, которые можно использовать для оптимизации вычислений. Например, симметричные матрицы имеют равные элементы относительно главной диагонали и могут быть более эффективно решены с использованием соответствующих алгоритмов.
Время решения матрицы зависит от сложности матрицы и используемого алгоритма. Некоторые матрицы можно решить с помощью простых методов, таких как метод Гаусса или метод простой итерации. Однако, для более сложных матриц может потребоваться применение более сложных алгоритмов, таких как метод LU-разложения или метод Холецкого.
Также важно учитывать вычислительные ресурсы, доступные для решения матрицы. На скорость решения матрицы может влиять процессор компьютера, объем оперативной памяти и другие факторы.
В итоге, сложность матрицы и время решения тесно связаны. Более сложные матрицы требуют больше времени для решения, а использование оптимизированных алгоритмов и вычислительных ресурсов может сократить время выполнения вычислений.
Влияние размерности матрицы на время решения
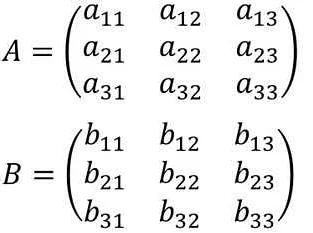
Время решения матрицы в математике зависит от ее размерности. Чем больше размерность матрицы, тем больше времени требуется для ее решения. Это связано с тем, что при увеличении размерности увеличивается количество элементов, которые необходимо обработать.
Решение матрицы включает в себя выполнение различных операций, таких как сложение, вычитание, умножение и деление элементов матрицы. Чем больше элементов в матрице, тем больше операций требуется для ее решения, и, соответственно, больше времени занимает выполнение этих операций.
Однако время решения матрицы не зависит только от ее размерности. Влияние на время решения также оказывают другие факторы, такие как алгоритм, используемый для решения матрицы, и характеристики аппаратного обеспечения, на котором выполняется вычисление. Некоторые алгоритмы могут быть более эффективными для решения матриц большой размерности, чем другие.
Важно учитывать размерность матрицы при планировании решения математических задач. Если размерность матрицы большая, то время, необходимое для ее решения, может быть значительным. В таких случаях может быть полезно применить оптимизационные методы или рассмотреть альтернативные подходы к решению задачи.
Таким образом, размерность матрицы имеет существенное влияние на время ее решения в математике. Чем больше размерность матрицы, тем больше времени требуется для ее решения. При планировании решения математических задач необходимо учитывать этот фактор и применять соответствующие оптимизационные методы, чтобы сократить время выполнения задачи.
Методы решения матрицы и их влияние на время
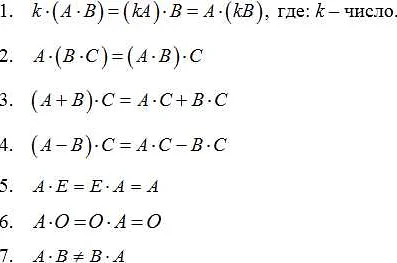
Одним из наиболее распространенных методов является метод Гаусса. Он основан на последовательном преобразовании исходной матрицы с помощью элементарных операций: сложение строк, умножение строки на число и перестановка строк. Метод Гаусса позволяет привести матрицу к треугольному виду и последовательно решить систему уравнений, начиная с последнего уравнения. Время решения матрицы с помощью метода Гаусса зависит от размерности матрицы и количества неизвестных переменных.
Другим известным методом решения матрицы является метод Жордана-Гаусса. Он является модификацией метода Гаусса и позволяет в процессе преобразования матрицы получить единичную матрицу на месте исходной. Этот метод обладает тем преимуществом, что позволяет найти обратную матрицу для исходной матрицы и решить систему уравнений сразу для нескольких значений вектора правой части. Однако, метод Жордана-Гаусса может быть более вычислительно затратным по времени, чем метод Гаусса, особенно при большом количестве неизвестных переменных.
Еще одним методом решения матрицы является метод Крамера. Он основан на вычислении определителей подматриц исходной матрицы. Метод Крамера позволяет найти численные значения неизвестных переменных, используя отношение определителей. Время решения матрицы с помощью метода Крамера может быть вычислительно затратным, особенно при большом размере матрицы и большом количестве неизвестных переменных.
Все перечисленные методы имеют свои достоинства и недостатки, и выбор оптимального метода решения матрицы зависит от конкретной задачи и требуемой точности результата. При выборе метода также следует учитывать ограничения по времени, так как время решения матрицы может значительно варьироваться в зависимости от выбранного метода и размерности матрицы.
Видео по теме:
Вопрос-ответ:
Какое время обычно занимает решение матрицы в математике?
Время, которое требуется для решения матрицы в математике, зависит от ее размеров и сложности. Обычно для матриц размером до 3×3 решение может занимать несколько секунд или даже меньше. Но с увеличением размеров матрицы время решения может значительно увеличиваться. Например, для матриц размером 1000×1000 или больше может потребоваться несколько минут или даже часов.
Есть ли способы ускорить процесс решения матрицы?
Да, существуют различные методы и алгоритмы, которые позволяют ускорить процесс решения матрицы. Например, метод Гаусса позволяет привести матрицу к ступенчатому виду и решить систему линейных уравнений более эффективно. Также можно использовать параллельные вычисления или специализированное аппаратное обеспечение, такое как графические процессоры (GPU), чтобы ускорить вычисления.
Как влияет размер матрицы на время ее решения?
Размер матрицы напрямую влияет на время ее решения. Чем больше размер матрицы, тем больше операций нужно выполнить для ее решения, и, соответственно, тем больше времени это займет. Например, для матриц размером 3×3 решение может занять всего несколько секунд, а для матриц размером 1000×1000 или больше — несколько минут или даже часов.
Можно ли сократить время решения матрицы, используя компьютер?
Да, использование компьютера может значительно сократить время решения матрицы. Компьютер может выполнить сложные вычисления гораздо быстрее, чем человек, и может использовать параллельные вычисления или специализированное аппаратное обеспечение для ускорения процесса. Также существуют специализированные программы и библиотеки для решения матриц, которые оптимизированы для быстрого выполнения вычислений.
Какие еще факторы могут влиять на время решения матрицы?
Кроме размера матрицы, время решения может зависеть от других факторов, таких как специфика задачи, наличие специальных структур в матрице (например, разреженности), выбранный метод решения, используемое аппаратное и программное обеспечение, а также качество и оптимизация реализации алгоритма. Все эти факторы могут влиять на производительность и время решения матрицы в математике.
Применение компьютерных программ для решения матрицы
В современном мире компьютерные программы стали неотъемлемой частью математических вычислений, в том числе и решения матриц. Программное обеспечение предоставляет мощные инструменты для работы с матрицами, которые позволяют эффективно и быстро находить решения.
Одним из самых популярных программных инструментов для работы с матрицами является язык программирования Python с его библиотекой numpy. Numpy предоставляет множество функций и методов для выполнения различных операций над матрицами, включая решение систем линейных уравнений с помощью метода Гаусса или LU-разложения.
Другой популярной программой для решения матриц является MATLAB, который обладает мощной функциональностью для работы с математическими вычислениями. MATLAB предоставляет широкий набор функций для операций над матрицами, включая решение систем линейных уравнений с помощью метода прогонки или QR-разложения.
Существуют также специализированные программы для решения матриц, например, Wolfram Mathematica или Maple. Они предоставляют широкие возможности для работы с матрицами и выполнения различных математических операций.
Применение компьютерных программ значительно упрощает решение матричных задач и позволяет экономить время. Благодаря возможностям программного обеспечения можно быстро выполнить сложные операции над матрицами и получить точное решение.
Однако, необходимо помнить, что выбор программы для решения матрицы зависит от конкретной задачи и требований пользователя. Кроме того, для эффективной работы с матрицами в программе необходимо иметь достаточные знания и навыки в области математики и программирования.
В итоге, применение компьютерных программ для решения матрицы является важным инструментом в современных математических расчетах и позволяет существенно ускорить и упростить процесс получения решений.
Советы по оптимизации времени решения матрицы
При работе с матрицей в математике существуют несколько полезных советов, которые помогут оптимизировать время ее решения:
| 1. Используйте эффективные алгоритмы: Выберите подходящий алгоритм для решения матрицы. Некоторые алгоритмы могут иметь лучшую временную сложность, что позволит вам решать матрицу быстрее. |
| 2. Оптимизируйте операции с матрицами: Избегайте лишних операций с матрицами. Перед выполнением операций проверьте, существуют ли более оптимальные способы выполнить задачу. |
| 3. Используйте параллельные вычисления: При наличии возможности используйте параллельные вычисления, чтобы ускорить процесс решения матрицы. Распределение работы между несколькими ядрами или процессами может значительно сократить время выполнения. |
| 4. Выбирайте подходящий формат хранения данных: Выберите наиболее подходящий формат хранения данных для матрицы. Некоторые форматы могут обеспечить более эффективное использование памяти и более быстрый доступ к элементам матрицы. |
| 5. Проверяйте возможность использования специализированных библиотек: Использование специализированных математических библиотек может значительно ускорить процесс решения матрицы. Эти библиотеки обычно содержат оптимизированные алгоритмы и функции для работы с матрицами. |
Применение этих советов поможет вам сократить время решения матрицы и повысить эффективность вашего математического моделирования.
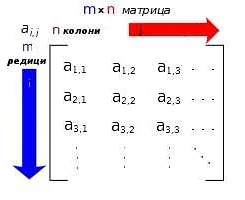


Очень интересная статья! Время прохождения матрицы в математике — это важный аспект, который необходимо учесть при решении задач. Часто ученики и студенты сталкиваются с тем, что у них не хватает времени на выполнение всех вычислений. Поэтому, знание эффективных методов и стратегий решения матрицы может значительно облегчить задачу. Я считаю, что такие статьи очень полезны, так как помогают найти оптимальные способы решения задач и сэкономить время. Буду ждать продолжения темы и новых советов!