Что значит маленькая 3 в математике

Маленькая 3 в математике может иметь несколько значений. Она может означать число три или быть обозначением для переменной или коэффициента. Узнайте, какие значения может иметь маленькая 3 в математике и как она используется в различных контекстах.

Число 3, хотя и кажется самым обычным и простым числом, имеет особое значение в математике. Оно встречается повсеместно и используется в различных математических концепциях, теориях и формулах.

Во-первых, число 3 является первым простым нечетным числом. Оно не делится на любое другое число, кроме 1 и самого себя. Благодаря этому свойству 3 играет важную роль в теории чисел и алгебре. Оно является основой для доказательства многих математических теорем и формул.

Кроме того, число 3 имеет свое значение в геометрии. Оно является числом сторон у треугольника – одной из самых фундаментальных геометрических фигур. Треугольники встречаются повсюду: от зданий и мостов до природных образований. Они имеют особые свойства и применяются в различных областях, таких как компьютерная графика, архитектура и физика.

Также число 3 играет важную роль в математической логике. Оно является основой для формулы триады, которая позволяет решать логические задачи и строить логические доказательства. Формула триады состоит из трех элементов: гипотезы, заключения и промежуточного утверждения. Она позволяет устанавливать логическую связь между различными утверждениями и делать выводы на основе заданных предпосылок.

В заключение, число 3 является одним из самых простых и одновременно важных чисел в математике. Оно имеет множество применений и играет ключевую роль в различных математических теориях и концепциях. Благодаря своим особенностям и свойствам, число 3 позволяет нам лучше понять и описать мир вокруг нас.

Начало и основы

В математике число 3 играет важную роль во многих областях. Оно используется в различных операциях, таких как сложение, вычитание, умножение и деление. Более того, оно является основой для создания других чисел и концепций.

Тройка также имеет множество уникальных свойств и характеристик. Например, она является первым нечётным простым числом и является основой для формирования других простых чисел. Она также является первым числом, образующим треугольник, и имеет связь с геометрическими фигурами, такими как треугольники и пирамиды.

В дополнение к этим математическим свойствам, число 3 имеет и другие значения и символические ассоциации. Оно используется в различных культурах и религиях как символ святой троицы, симметрии и гармонии. Тройка также часто ассоциируется с удачей, полнотой и совершенством.

Таким образом, число 3 играет важную роль в математике и имеет широкий спектр значений и свойств. Оно является началом и основой для многих математических концепций и операций, а также имеет глубокие символические значения.

Тройка в геометрии: симметрия и структура

Треугольник состоит из трех сторон и трех углов, которые образуются между этими сторонами. Он является самой простой фигурой, но при этом обладает множеством свойств и особенностей, которые играют важную роль в геометрии.

Треугольник обладает симметрией относительно своих сторон и углов. Он может быть равносторонним, когда его все стороны равны, или разносторонним, когда стороны разной длины. Треугольник также может быть равнобедренным, когда две его стороны равны, или разносторонним, когда все три стороны различны. Кроме того, треугольник может быть прямоугольным, когда один из его углов равен 90 градусам, или непрямоугольным, когда все его углы различны.

Треугольник также используется в геометрии для построения других фигур и определения их свойств. Например, при помощи треугольника можно построить прямоугольник, квадрат, ромб, пятиугольник и так далее. Кроме того, треугольник играет важную роль в теореме Пифагора и других фундаментальных теоремах геометрии.

Типы треугольниковСвойства

Равносторонний треугольник	Все стороны равны
Разносторонний треугольник	Все стороны разные
Равнобедренный треугольник	Две стороны равны
Прямоугольный треугольник	Один угол равен 90 градусам
Непрямоугольный треугольник	Все углы разные

Таким образом, тройка играет важную роль в геометрии, символизируя симметрию и структуру. Она является основой для изучения различных фигур и определения их свойств.

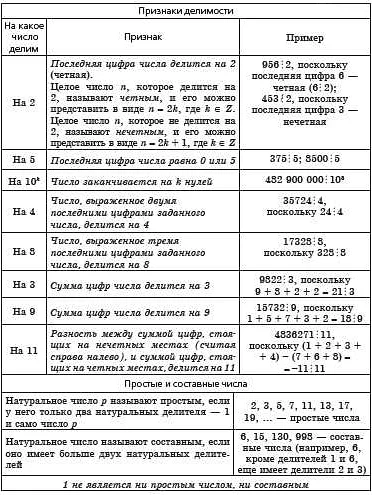
Три в арифметике: деление и доли

Когда мы говорим о делении, число 3 является одним из основных делителей многих чисел. Оно подразумевает равное распределение целого числа на три равные части. Например, если у нас есть 9 яблок, мы можем разделить их на 3 группы по 3 яблока в каждой.

Также число 3 часто используется в понятии доли или долях. Доля представляет собой часть от целого числа, и число 3 может быть использовано для обозначения одной из этих долей. Например, если мы говорим о трети от пирога, то мы имеем в виду одну из трех равных частей пирога.

Более того, число 3 имеет особенное значение в десятичной системе. Оно является одной из базовых цифр, которые составляют все остальные числа. Вместе с цифрами 0-9, число 3 играет важную роль в представлении и выполнении математических операций.

В заключение, число 3 имеет значительное значение в арифметике, особенно в отношении деления и долей. Оно является одним из основных делителей и может быть использовано для обозначения доли от целого числа. Кроме того, число 3 является базовой цифрой в десятичной системе, что делает его важным элементом в математических вычислениях.

Тройка в комбинаторике: возможности и варианты

В математике число 3 играет важную роль, особенно в комбинаторике. Комбинаторика изучает различные варианты и перестановки объектов, и тройка дает нам множество интересных возможностей.

Первая и самая простая возможность — это комбинация из трех элементов. Мы можем выбрать любые три элемента из заданного множества и создать комбинацию, которая будет уникальной и не повторяющейся.

Тройка также может представлять собой последовательность действий или событий. Например, мы можем представить трехэтапный процесс или трехшаговый алгоритм.

Кроме того, тройка может быть использована для задания трехмерных координат в пространстве. В трехмерной геометрии, тройка чисел может определить положение точки в пространстве.

Тройка также является основой для многих других математических понятий и концепций. Например, в теории вероятности мы можем говорить о трех вариантах исхода события — вероятность наступления, вероятность ненаступления и вероятность их объединения.

Таким образом, тройка в комбинаторике предоставляет нам множество возможностей и вариантов, которые можно использовать для решения различных математических задач и проблем.

Три в статистике: медиана и среднее значение

Число 3 играет важную роль в статистике, особенно при вычислении мер центральной тенденции, таких как медиана и среднее значение.

Медиана — это значение, которое делит упорядоченный набор данных на две равные части. Если в наборе данных есть нечетное количество чисел, то медиана будет просто центральным числом. Например, в наборе данных {1, 2, 3, 4, 5} медиана будет равна 3. Если в наборе данных четное количество чисел, то медиана будет равна среднему арифметическому двух центральных чисел. Например, в наборе данных {1, 2, 3, 4, 5, 6} медиана будет равна (3 + 4) / 2 = 3.5.

Среднее значение — это сумма всех чисел в наборе данных, разделенная на их общее количество. Например, для набора данных {1, 2, 3, 4, 5} среднее значение будет равно (1 + 2 + 3 + 4 + 5) / 5 = 3.

Интересно, что число 3 встречается в обеих мерах центральной тенденции — медиане и среднем значении. Это связано с тем, что число 3 является центральным числом в наборе данных {1, 2, 3, 4, 5}, а также является равным среднему значению всех чисел в этом наборе данных.

Тройственность в логике и философии

В математике число 3 играет важную роль, однако его значение не ограничивается только этой областью. Троечность также находит свое применение в логике и философии.

В логике тройственность означает наличие трех возможных значений для логического выражения: истина, ложь и непринадлежность. Это означает, что высказывание может быть не только истинным или ложным, но также может быть неопределенным или не принадлежащим ни одному из двух классов. Тройственность позволяет учесть сложность реального мира, где некоторые вопросы могут оставаться открытыми и не иметь однозначного ответа.

В философии тройственность часто ассоциируется с понятием трех миров. Согласно этому учению, мир можно разделить на три составляющие: мир разума, мир духа и мир материи. Такая тройственность позволяет лучше понять природу реальности и ее разнообразие.

Тройственность в логике и философии демонстрирует, что число 3 имеет глубокий смысл и широкое применение в различных областях знания. Оно позволяет учесть сложность и многообразие мира, а также раскрыть новые аспекты истины.

Третий разряд: системы счисления и числа

В десятичной системе счисления третий разряд является разрядом сотен. Это значит, что цифра, стоящая в третьем разряде, определяет количество сотен в числе. Например, если третий разряд числа равен 3, то это означает, что в числе содержится 3 сотни.

Однако третий разряд имеет значение и в других системах счисления. Например, в двоичной системе счисления третий разряд является разрядом четвертой степени двойки. Таким образом, цифра, стоящая в третьем разряде, определяет значение четвертой степени двойки в числе.

Также третий разряд имеет значение в системе счисления с основанием 3. В этой системе третий разряд является разрядом девятой степени тройки. Таким образом, цифра, стоящая в третьем разряде, определяет значение девятой степени тройки в числе.

Третий разряд в системах счисления является одним из основных элементов, определяющих значение числа. Он влияет на позиционный вес цифры в числе и позволяет определить, сколько раз определенная цифра повторяется в числе. Именно поэтому третий разряд имеет такое большое значение в математике и системах счисления.

Завершение: символика и значение

Во-первых, число 3 является самым маленьким простым числом. Оно не делится нацело ни на одно другое число, кроме единицы и самого себя. Это делает число 3 особенным и уникальным.

Во-вторых, число 3 является числом треугольника. Треугольник — это геометрическая фигура, которая имеет три стороны и три угла. Таким образом, число 3 символизирует гармонию и баланс в геометрии.

Кроме того, число 3 часто используется в различных аспектах жизни. Например, у нас есть три измерения пространства (длина, ширина и высота), три временные измерения (прошлое, настоящее и будущее) и три основных цвета (красный, желтый и синий).

В заключение, число 3 играет важную роль в математике и символизирует уникальность, баланс и гармонию. Оно является одним из фундаментальных чисел, которые лежат в основе многих математических концепций и теорий. Поэтому нельзя недооценивать значение и важность числа 3 в математике.

Вопрос-ответ:

Зачем в математике нужна цифра 3?

Цифра 3 имеет большое значение в математике, так как она является одной из основных цифр, символизирующих количество и порядок. Она используется в различных арифметических операциях, в тригонометрии, в числовых системах и во многих других математических концепциях.

Какую роль играет число 3 в геометрии?

Число 3 играет важную роль в геометрии, так как оно соответствует числу углов в треугольнике. Треугольник является одним из основных геометрических объектов и его свойства исследуются во многих областях математики.

Какое значение имеет число 3 в теории вероятности?

В теории вероятности число 3 играет роль количества возможных исходов в некоторых ситуациях. Например, при броске обычного кубика с числами от 1 до 6, вероятность выпадения числа 3 равна 1/6. Также число 3 может использоваться для представления количества событий в некоторых случайных экспериментах или в задачах с дискретным распределением.

Почему третья степень числа имеет особое значение в математике?

Третья степень числа имеет особое значение в математике, потому что она является первой нечетной степенью и имеет свои уникальные свойства. Например, возведение числа в третью степень является операцией кубирования и используется для нахождения объема кубических фигур. Кроме того, третья степень может быть использована для решения некоторых уравнений и задач, связанных с трехмерным пространством.

Как число 3 связано с разложением чисел на простые множители?

Число 3 имеет важное значение в разложении чисел на простые множители. Если число делится на 3 без остатка, то 3 является одним из простых множителей этого числа. Например, число 9 можно разложить на простые множители в виде 3 * 3. Также число 3 играет роль в определении того, является ли число простым или составным, так как оно является одним из первых простых чисел.

Зачем в математике используется число 3?

Число 3 является одним из основных чисел в математике и имеет множество применений. Оно используется для обозначения количества элементов в некоторых множествах, например, трехугольников или трехмерных фигур. Также число 3 используется во многих математических формулах и уравнениях, включая тригонометрические функции, геометрию и алгебру. Кроме того, число 3 имеет символическое значение в различных контекстах, так как оно образует базис для многих других чисел, таких как 30, 300, 3000 и т.д.

Какое значение имеет число 3 в геометрии?

В геометрии число 3 имеет особое значение, так как оно обозначает количество сторон в треугольнике. Треугольник является одной из основных фигур в геометрии, и его свойства и формулы тесно связаны с числом 3. Кроме того, число 3 также используется для обозначения трехмерных фигур, таких как куб или пирамида, которые имеют по три ребра, вершины и грани. Таким образом, число 3 является ключевым элементом в геометрии и позволяет нам понять и анализировать различные геометрические объекты.

Видео по теме: