Объяснение понятия кратных чисел в математике для пятого класса
Содержимое
- 1 Объяснение понятия кратных чисел в математике для пятого класса
- 1.1 Кратные числа: основные понятия и примеры
- 1.2 Видео по теме:
- 1.3 Что такое кратные числа в математике
- 1.4 Понятие кратности чисел и свойства кратных чисел
- 1.5 Вопрос-ответ:
- 1.5.0.1 Как определить, является ли число кратным другому числу?
- 1.5.0.2 Как найти все кратные числа для данного числа?
- 1.5.0.3 Как найти минимальное общее кратное двух чисел?
- 1.5.0.4 Как связаны кратные числа и делители?
- 1.5.0.5 Как использовать знание о кратных числах в повседневной жизни?
- 1.5.0.6 Что такое кратные числа?
- 1.6 Как определить, является ли число кратным
- 1.7 Примеры кратных чисел и их свойств
- 1.8 Как найти все кратные числа для заданного числа
- 1.9 Значение кратных чисел в решении задач
- 1.10 Интересные факты о кратных числах
Кратные числа в математике 5 — это числа, которые делятся на другое число без остатка. Узнайте, как определить кратность числа и как это применяется в различных задачах и уравнениях. Познакомьтесь с правилами и примерами для понимания кратности чисел в пятом классе математики.
Кратные числа — это числа, которые делятся на другое число без остатка. В математике кратные числа являются важной темой, которая помогает нам понять основы деления и множества чисел.
Когда одно число делится на другое без остатка, это означает, что первое число является кратным второго числа. Например, число 10 является кратным числа 5, потому что оно делится на 5 без остатка.
Знание кратных чисел помогает нам решать задачи в математике, такие как нахождение наименьшего общего кратного (НОК) или определение кратности чисел в последовательностях. Кратные числа также используются в различных областях науки и техники, например, в электричестве и физике.
Важно отметить, что кратные числа всегда положительные. Например, -10 и -5 также являются кратными числа 5, но они отрицательны.
Чтобы определить, является ли одно число кратным другого, можно просто проверить, делится ли оно на другое число без остатка. Если делится, то первое число является кратным второго числа, в противном случае они не являются кратными.
Кратные числа: основные понятия и примеры
Для определения, является ли число кратным другому числу, используется понятие деления с остатком. Если при делении одного числа на другое остаток равен нулю, то число является кратным.
Например:
- Число 10 кратно числу 2, так как 10 делится на 2 без остатка.
- Число 15 кратно числу 3, так как 15 делится на 3 без остатка.
- Число 21 кратно числу 7, так как 21 делится на 7 без остатка.
Кратные числа имеют ряд интересных свойств. Например, если число a кратно числу b, то числа a и b имеют общий делитель – число b.
Знание понятия кратных чисел полезно в математике для работы с дробями, нахождения наименьшего общего кратного и других задач.
Видео по теме:
Что такое кратные числа в математике
Кратными числами называются числа, которые делятся на другое число без остатка. В математике этот процесс называется делением с остатком. Если одно число делится на другое без остатка, то первое число называется кратным второму числу.
Простым примером кратных чисел являются часы. Если часы показывают 12, то это означает, что текущее время кратно 12. Аналогично, если минутная стрелка указывает на 30, это означает, что прошло 30 минут, то есть время кратно 30 минутам.
Для того чтобы проверить, является ли одно число кратным другому, можно воспользоваться делением с остатком. Если при делении одного числа на другое получается 0 в остатке, то первое число является кратным второму числу. Например, число 15 является кратным числу 3, так как 15 / 3 = 5 без остатка.
Кратные числа широко применяются в различных областях математики и науки. Они позволяют упростить вычисления и анализировать различные паттерны и связи между числами.
Примеры кратных чисел:
- Число 10 кратно числу 2, так как 10 / 2 = 5 без остатка.
- Число 20 кратно числу 4, так как 20 / 4 = 5 без остатка.
- Число 36 кратно числу 6, так как 36 / 6 = 6 без остатка.
Знание о кратных числах поможет вам лучше понимать и использовать математические концепции и решать различные задачи.
Понятие кратности чисел и свойства кратных чисел
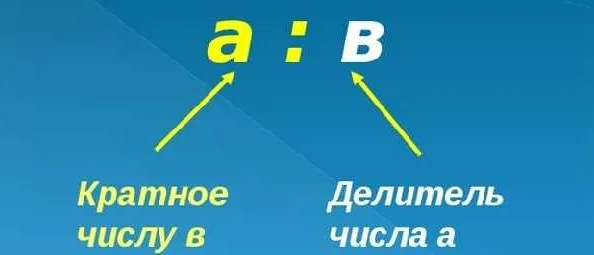
Например, число 10 является кратным числом числа 5, так как оно делится на 5 без остатка. В этом случае число 5 является множителем числа 10.
Свойства кратных чисел также играют важную роль в математике. Некоторые из них включают:
СвойствоОписание
| 1 | Любое число является кратным самого себя. |
| 2 | Если число делится на другое число, а другое число делится на третье число, то первое число также делится на третье число. |
| 3 | Если число делится на другое число, а другое число делится на это же число, то первое число также делится на это же число. |
| 4 | Если число делится на два числа, то оно также делится на их наименьшее общее кратное (НОК). |
| 5 | Если число делится на два числа, то оно также делится на их наибольший общий делитель (НОД). |
Понимание понятия кратности чисел и свойств кратных чисел играет важную роль в решении различных математических задач и применении в реальном мире.
Вопрос-ответ:
Как определить, является ли число кратным другому числу?
Чтобы определить, является ли число кратным другому числу, нужно проверить, делится ли оно на это число без остатка. Если делится без остатка, то число является кратным.
Как найти все кратные числа для данного числа?
Чтобы найти все кратные числа для данного числа, нужно последовательно умножать его на натуральные числа. Например, для числа 4 все кратные числа будут: 4, 8, 12, 16, и т.д.
Как найти минимальное общее кратное двух чисел?
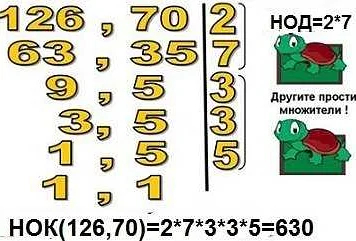
Чтобы найти минимальное общее кратное двух чисел, нужно найти их наименьшее общее кратное (НОК). Это можно сделать с помощью алгоритма Евклида или с помощью разложения чисел на простые множители.
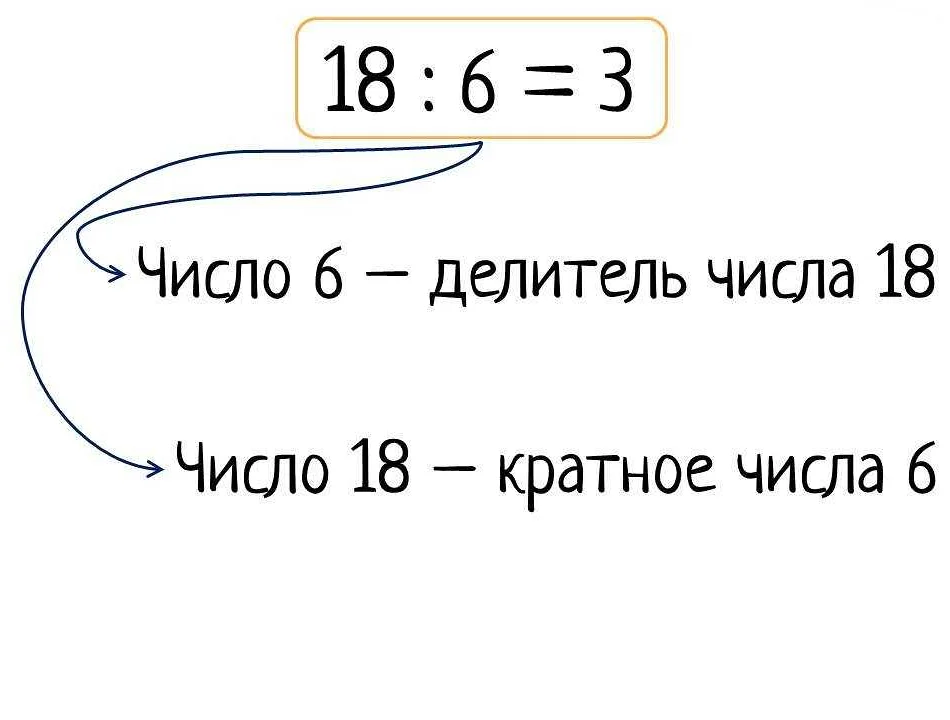
Как связаны кратные числа и делители?
Кратные числа являются результатом умножения числа на его делители. Если число делится на другое число без остатка, то оно является кратным этому числу.
Как использовать знание о кратных числах в повседневной жизни?
Знание о кратных числах может быть полезным во многих ситуациях. Например, оно может помочь в расчете времени, скорости, размещении предметов в пространстве и т.д. Также знание о кратных числах может быть полезным при работе с денежными суммами, ведь некоторые купюры имеют номиналы, являющиеся кратными другим номиналам.
Что такое кратные числа?
Кратные числа — это числа, которые делятся на данное число без остатка.
Как определить, является ли число кратным
Например, 10 делится на 5 без остатка, так как 10 ÷ 5 = 2. Поэтому число 10 является кратным числу 5. Если бы результат деления был не целым числом, например, 10 ÷ 3 = 3.3333, то число 10 не являлось бы кратным числу 3.
Обычно используются такие математические обозначения: если число а делится на число b без остатка, то говорят, что а является кратным числа b. Это обозначается следующим образом: а ≡ 0 (mod b), где знак «≡» означает «равно» и «mod» – это аббревиатура от английского слова «modulo», что означает «по модулю».
Таким образом, если при делении числа а на число b остаток равен нулю, то можно с уверенностью сказать, что а является кратным числа b.
Примеры кратных чисел и их свойств
Пример 1: Число 4 является кратным числом числа 2, так как 2 умноженное на 2 дает 4.
Пример 2: Число 15 является кратным числом числа 3, так как 3 умноженное на 5 дает 15.
Пример 3: Число 100 является кратным числом числа 10, так как 10 умноженное на 10 дает 100.
Свойства кратных чисел:
Свойство 1: Если число a кратно числу b, то любое кратное числа a также будет кратно числу b.
Свойство 2: Если число a кратно числу b и число b кратно числу c, то число a также будет кратно числу c.
Свойство 3: Если число a кратно числу b, то число b также является делителем числа a.
Использование кратных чисел позволяет упростить многие математические задачи и вычисления. Они активно применяются в алгебре, арифметике, физике и других науках.
Как найти все кратные числа для заданного числа
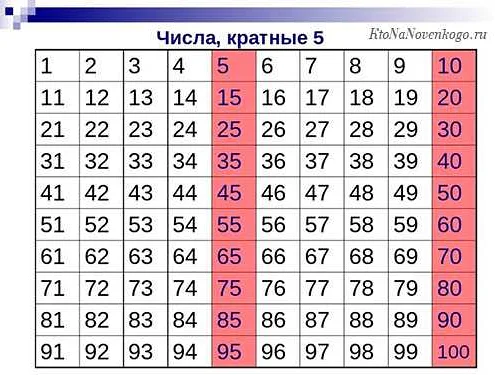
Для начала, выберите число для которого вы хотите найти кратные числа. Затем можно последовательно увеличивать числа и проверять их на кратность выбранному числу.
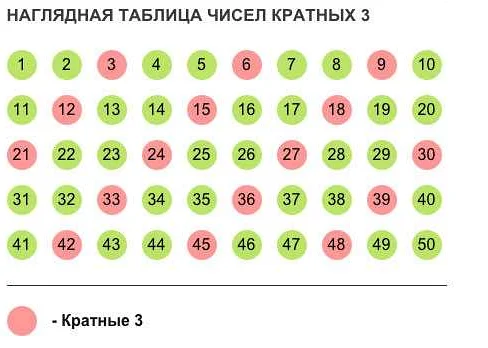
Пример: Пусть мы хотим найти все кратные числа для числа 3. Мы начинаем с 0 и последовательно увеличиваем число на 1. Проверяем каждое число на кратность 3. Если число делится на 3 без остатка, то оно является кратным числом для числа 3.
Таким образом, все кратные числа для числа 3 будут следующими:
- 0
- 3
- 6
- 9
- 12
- 15
- …
При необходимости можно ограничить поиск кратных чисел до определенного интервала или задать другие условия для поиска.
Найденные кратные числа могут быть использованы для решения различных задач и применений в математике и других науках.
Значение кратных чисел в решении задач

Кратные числа играют важную роль в решении различных математических задач. Кратность числа позволяет нам определить, делится ли одно число на другое без остатка.
Значение кратных чисел особенно полезно при решении задач, связанных с распределением и делением предметов или объектов. Например, если нам нужно разделить 12 яблок поровну между 4 детьми, мы можем использовать понятие кратности, чтобы определить, сколько яблок получит каждый ребенок.
Для этого мы можем проверить, является ли число 12 кратным числу 4. Если да, то мы можем разделить яблоки поровну между детьми, каждому достанется по 3 яблока. Если число не является кратным, то неравномерное распределение будет означать, что каждый ребенок получит разное количество яблок.
Кратные числа также могут быть полезны при решении задач, связанных с нахождением наименьшего общего кратного (НОК) или наибольшего общего делителя (НОД) двух или нескольких чисел. Эти понятия можно использовать для упрощения вычислений и нахождения оптимальных решений.
Интересные факты о кратных числах

Вот несколько интересных фактов о кратных числах:
1. Сумма двух кратных чисел также является кратной числом.
Если a и b являются кратными числами для числа c, то их сумма a + b также будет кратной числом c. Например, если 6 и 9 являются кратными числами для числа 3, то их сумма 6 + 9 = 15 также будет кратной числу 3.
2. Произведение двух кратных чисел также является кратным числом.
Если a и b являются кратными числами для числа c, то их произведение a * b также будет кратным числом c. Например, если 4 и 5 являются кратными числами для числа 2, то их произведение 4 * 5 = 20 также будет кратным числу 2.
3. Кратные числа могут использоваться для определения цикличности.
Кратные числа часто используются для определения цикличности некоторых явлений. Например, если мы наблюдаем, что событие повторяется каждые 6 дней, то мы можем заключить, что оно является кратным числом 6.
4. Нуль является кратным числом для любого числа.
Нуль является кратным числом для любого натурального числа. Это означает, что любое число можно разделить на ноль без остатка.
Изучение кратных чисел помогает нам понять и анализировать различные математические и физические явления. Они широко используются в различных областях науки и техники для моделирования и предсказания различных процессов.
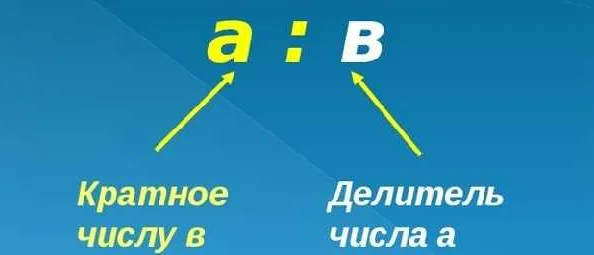

Кратные числа в математике — это числа, которые делятся на другое число без остатка. Например, если число делится на 5 без остатка, то оно является кратным числом для числа 5. Также можно сказать, что кратное число умножено на другое число даёт исходное число. Например, 5 умножить на 3 равно 15, а это значит, что 15 является кратным числом для 5. Кратные числа широко используются в математике для решения различных задач и упрощения вычислений. Понимание этого понятия поможет вам лучше понять и применять математические операции в повседневной жизни.
Кратные числа – это такие числа, которые делятся на другое число без остатка. Например, если мы рассматриваем кратные числа 5, то это будут числа, которые делятся на 5 без остатка: 5, 10, 15, 20 и так далее. Кратные числа можно найти, умножив число, на которое они кратны, на любое целое число. Например, если мы хотим найти кратные числа 5, мы можем умножить 5 на 1, получим 5, умножить на 2, получим 10 и так далее. Кратные числа широко используются в математике и имеют важное значение в различных областях, включая алгебру и арифметику. Они помогают нам понять и изучать закономерности чисел и решать различные задачи.
Очень интересная статья! Я всегда задавалась вопросом, что такое кратные числа. Чтение этой статьи помогло мне разобраться в этом понятии. Кратные числа — это числа, которые делятся на другое число без остатка. Например, если число A делится на число B без остатка, то A будет кратным числом B. Например, 10 кратно 2, так как 10 делится на 2 без остатка. Это понятие очень полезно в математике, так как позволяет нам находить общие закономерности и упрощать вычисления. Спасибо за статью, теперь я лучше понимаю, что такое кратные числа и как их использовать в задачах.
Кратные числа в математике — это числа, которые делятся на другое число без остатка. Например, если мы рассматриваем число 5, то его кратными будут числа 10, 15, 20 и так далее. Важно отметить, что кратные числа всегда больше или равны числу, на которое они кратны. Кратные числа имеют свои особенности и приложения в разных областях науки и техники. Например, в физике они используются для вычисления периодических явлений и колебаний. Знание кратных чисел полезно не только в математике, но и в повседневной жизни. Оно помогает нам понять, как устроен мир вокруг нас и решать различные задачи, связанные с количеством и порядком.