Угловые скобки в математике что означают

Угловые скобки в математике являются символами, которые используются для обозначения различных математических операций и выражений. Узнайте, какие значения могут иметь угловые скобки и как они используются в различных областях математики.

Угловые скобки – это один из основных символов, используемых в математике. Они имеют важное значение и используются для обозначения различных математических операций и конструкций.

Одним из основных использований угловых скобок является обозначение углов. Угол обычно обозначается тремя точками и помещается между угловыми скобками. Например, 〈ABC〉 – обозначение угла ABC.

Также угловые скобки используются для обозначения векторов. Вектор – это направленный отрезок, который имеет длину и направление. Обозначение вектора часто осуществляется с помощью угловых скобок. Например, 〈a, b, c〉 – обозначение вектора ABC, где a, b и c – координаты вектора в трехмерном пространстве.

Кроме того, угловые скобки используются для обозначения множеств. Множество – это совокупность элементов, объединенных общим свойством. Обозначение множества также осуществляется с помощью угловых скобок. Например, 〈1, 2, 3〉 – обозначение множества, содержащего элементы 1, 2, 3.

Таким образом, угловые скобки в математике имеют различные значения и используются для обозначения углов, векторов и множеств. Корректное использование угловых скобок позволяет более точно и ясно записывать и передавать математические выражения и конструкции.

Роль угловых скобок в математических выражениях

Угловые скобки в математике имеют большое значение и используются для различных целей. Они могут быть использованы для обозначения углов, но чаще всего встречаются в качестве математических символов.

В математических выражениях угловые скобки обычно используются для группировки операций и указания порядка выполнения действий. Они помогают определить, какие операции должны быть выполнены первыми.

Например, в выражении (3 + 5) * 2 угловые скобки вокруг суммы 3 + 5 указывают, что эта операция должна быть выполнена перед умножением на 2. Без скобок это выражение будет означать умножение 5 на 2, а затем сложение с 3, что даст неверный результат.

Угловые скобки также могут использоваться для обозначения интервалов или множеств. Например, (0, 1) обозначает интервал чисел от 0 до 1, не включая граничные значения.

Кроме того, угловые скобки могут использоваться для указания значений параметров функций. Например, в функции f(x) угловые скобки вокруг x обозначают, что x является параметром функции.

Все эти примеры показывают, что угловые скобки играют важную роль в математических выражениях, позволяя определить порядок выполнения операций, обозначить интервалы и множества, а также указать параметры функций.

Видео по теме:

Перечень арифметических операций, где используются угловые скобки

Угловые скобки в математике могут использоваться в различных арифметических операциях. Вот несколько примеров:

1. Неравенство: Угловые скобки применяются для указания неравенства между двумя числами или выражениями. Например, выражение a < b означает, что число a меньше числа b.

2. Математическое выражение: Угловые скобки могут использоваться для обозначения математического выражения. Например, выражение <x + 2y> обозначает сумму чисел x и 2y.

3. Угловые скобки в векторах: Векторы в математике могут быть обозначены с помощью угловых скобок. Например, вектор <a, b, c> состоит из трех элементов a, b и c.

4. Угловые скобки в матрицах: Матрицы в математике также могут быть представлены с использованием угловых скобок. Например, матрица <1, 2, 3> может быть представлена в виде строки из трех элементов или как матрица размером 1×3.

Угловые скобки в математике имеют различные значения и используются в различных контекстах. Важно правильно интерпретировать их в каждом конкретном случае для понимания математических операций и выражений.

Угловые скобки в геометрии и тригонометрии

Угловые скобки также широко используются в геометрии и тригонометрии для обозначения углов и тригонометрических функций.

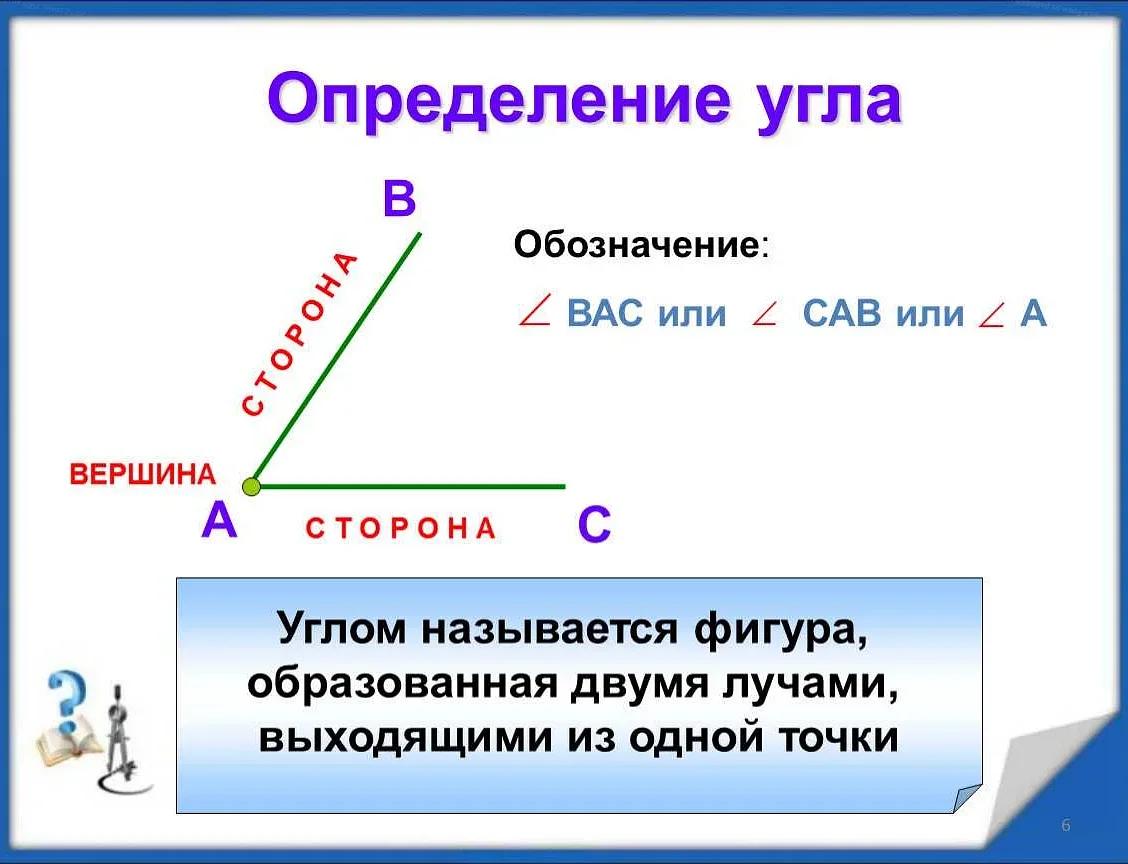
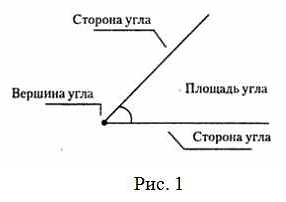
В геометрии угловые скобки используются для обозначения углов. Угол состоит из двух лучей, называемых сторонами угла, и начальной точки, называемой вершиной угла. Угловые скобки ставятся между сторонами угла и указывают на его меру. Например, 〈ABC обозначает угол ABC.

В тригонометрии угловые скобки используются для обозначения тригонометрических функций. Тригонометрические функции связаны с углами и используются для решения различных задач в геометрии и физике. Угловые скобки ставятся перед аргументом функции. Например, 〈sin(x) обозначает синус угла x.

Угловые скобки в геометрии и тригонометрии играют важную роль в обозначении углов и тригонометрических функций. Они помогают нам точно указать, о каком угле или функции идет речь и упрощают запись математических выражений.

Вопрос-ответ:

Какое значение имеют угловые скобки в математике?

Угловые скобки в математике используются для обозначения углов и интервалов, а также для обозначения операций и выражений.

Какие операции могут быть обозначены с помощью угловых скобок?

Угловые скобки могут обозначать операции, такие как сумма (символ ∑), произведение (символ ∑), скалярное произведение (символ ⋅), и многие другие.

Какие значения могут быть записаны в угловых скобках?

В угловых скобках могут быть записаны углы (в градусах или радианах), числа, выражения, функции и многие другие значения. Значение зависит от контекста использования угловых скобок.

Какие интервалы могут быть обозначены с помощью угловых скобок?

Угловые скобки могут обозначать открытые и замкнутые интервалы, например (a, b) или [a, b]. Открытый интервал не включает конечные точки, а замкнутый интервал включает их.

Можно ли использовать угловые скобки в выражениях для обозначения приоритета операций?

Да, угловые скобки могут использоваться в выражениях для обозначения приоритета операций. Выражение, заключенное в угловые скобки, будет вычислено в первую очередь.

Какое значение имеют угловые скобки в математике?

Угловые скобки в математике обычно используются для обозначения углов, но они также имеют другие значения и применения.

В каких случаях угловые скобки используются в математике?

Угловые скобки в математике используются для обозначения углов, для обозначения множеств, для обозначения операций с векторами, для обозначения скалярного произведения и других математических операций.

Алгебраические выражения с угловыми скобками

Угловые скобки в математике используются для оформления алгебраических выражений, обозначающих операции или группы операций, которые нужно выполнить в первую очередь.

В алгебраических выражениях угловые скобки могут быть использованы, чтобы выделить часть выражения и сделать ее более явной. Например, выражение (a + b) * c означает, что сначала нужно выполнить операцию сложения a + b, а затем результат умножить на число c. Без скобок это выражение может быть неправильно интерпретировано как a + (b * c), что даст другой результат.

Угловые скобки также могут быть использованы для оформления выражений с переменными. Например, выражение x < 10 означает, что переменная x должна быть меньше числа 10.

Кроме того, угловые скобки могут использоваться в математических функциях и операциях. Например, функция округления числа round() может быть записана как <round>(x).

Использование угловых скобок в алгебраических выражениях позволяет упростить и улучшить читаемость математических формул и выражений, а также избежать путаницы и неправильного их толкования.

Использование угловых скобок в логических операциях

В математике угловые скобки (<>) имеют особое значение и часто используются для обозначения интервалов или диапазонов чисел. Однако, они также могут быть использованы в логических операциях для задания условий и проверки истинности выражений.

В логических операциях угловые скобки могут быть использованы для обозначения операторов сравнения. Например, выражение x < y означает, что значение переменной x меньше значения переменной y. В этом случае, угловые скобки используются для обозначения оператора «меньше» (<) и указывают на то, что значение переменной x должно быть меньше значения переменной y.

Также, угловые скобки можно использовать для обозначения операторов «больше» (>), «меньше или равно» (<=) и «больше или равно» (>=). Например, выражение x >= 10 означает, что значение переменной x должно быть больше или равно 10.

Угловые скобки также могут быть использованы в комбинации с другими логическими операторами, такими как «и» (&&) и «или» (||). Например, выражение (x > 0) && (y < 10) означает, что значение переменной x должно быть больше 0 и значение переменной y должно быть меньше 10.

Использование угловых скобок в логических операциях позволяет создавать сложные условия, которые могут быть использованы для принятия решений в программировании или в других областях, где требуется логическое мышление.

Матрицы и угловые скобки

Матрицы обычно записываются с использованием угловых скобок. Например, матрица размером 2×2 может быть записана следующим образом:

A = [ a11 a12 ]

[ a21 a22 ]

Здесь каждый элемент матрицы обозначается как aij, где i — номер строки, а j — номер столбца. Для обозначения элементов матрицы иногда также используются круглые скобки или квадратные скобки, но угловые скобки являются наиболее распространенным обозначением.

Угловые скобки также используются в некоторых случаях для обозначения операций над матрицами. Например, если A и B — матрицы одинакового размера, то их сумма может быть записана как:

A + B = [ a11 + b11 a12 + b12 ]

[ a21 + b21 a22 + b22 ]

Здесь каждый элемент суммы обозначается как сумма соответствующих элементов матриц A и B.

Таким образом, угловые скобки в математике играют важную роль в обозначении и операциях с матрицами. Они помогают упростить запись и понимание матричных операций, а также являются удобным инструментом при работе с линейными уравнениями и линейными отображениями.

Угловые скобки в программировании

В HTML и XML, угловые скобки используются для обозначения тегов. Например:

ПримерОписание

<p>Текст</p>	Открывающий и закрывающий теги параграфа
<a href=»https://example.com»>Ссылка</a>	Открывающий и закрывающий теги гиперссылки с атрибутом href

В языках программирования, таких как C++, Java, C#, угловые скобки используются для обозначения шаблонов (generics). Например:

ПримерОписание

std::vector<int> numbers;	Создание вектора чисел с использованием шаблона int
List<String> strings = new List<>();	Создание списка строк с использованием шаблона String

Угловые скобки также могут использоваться в математических выражениях или в операциях сравнения во многих языках программирования. Например:

ПримерОписание

if (x < y)	Сравнение значений переменных x и y
int result = (a + b) * c;	Вычисление значения выражения (a + b) * c

Важно помнить, что в разных языках программирования синтаксис и использование угловых скобок могут незначительно отличаться. Поэтому важно ознакомиться с документацией конкретного языка программирования для более детальной информации о том, как использовать угловые скобки в определенном контексте.