Что такое золотая середина в математике

Золотая середина в математике – это концепция, описывающая оптимальное соотношение между двумя крайностями. В математике, золотая середина может быть применена к различным аспектам, таким как оптимизация функций, нахождение баланса между точностью и простотой, и т.д. Узнайте больше о золотой середине в математике и ее применении в данной статье.

Золотая середина в математике — это принцип, основанный на нахождении оптимального баланса между двумя крайностями. В математике это означает, что для достижения наилучших результатов необходимо выбрать оптимальное значение из множества возможных. Этот принцип широко используется в различных областях математики, включая геометрию, алгебру и статистику.

Одним из примеров золотой середины является поиск оптимального значения функции. Если значение функции слишком мало, это может указывать на недостаточную точность или неполное представление данных. С другой стороны, если значение функции слишком большое, это может указывать на избыточность данных или неправильное моделирование. Поэтому необходимо найти такое значение функции, которое находится в золотой середине между этими двумя крайностями.

Например, при решении задачи оптимизации, важно найти такое значение переменной, которое минимизирует или максимизирует целевую функцию. Если выбрать слишком маленькое значение, то решение будет недостаточно точным, а слишком большое значение может привести к неправильным результатам. Поэтому необходимо найти золотую середину, где значение переменной оптимально для достижения наилучших результатов.

Золотая середина также применяется в математической моделировании, чтобы найти баланс между точностью и вычислительной сложностью. Если модель слишком простая, она может упускать некоторые важные детали и давать неточные результаты. С другой стороны, слишком сложная модель может быть трудной для вычисления и требовать больших вычислительных ресурсов. Поэтому необходимо найти золотую середину, где модель достаточно точна, но при этом не слишком сложна для вычисления.

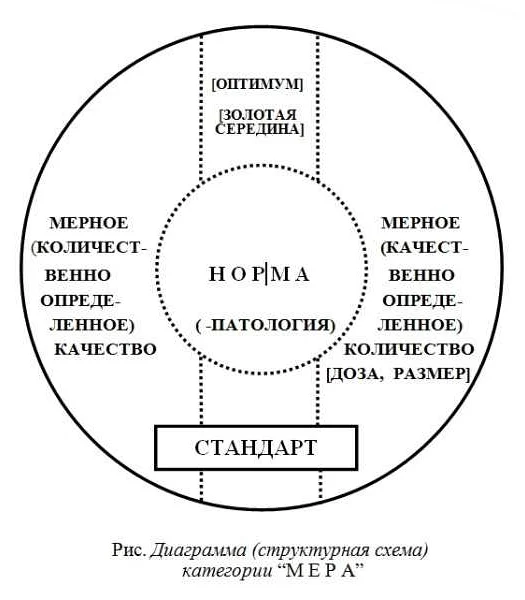
Что такое золотая середина в математике?

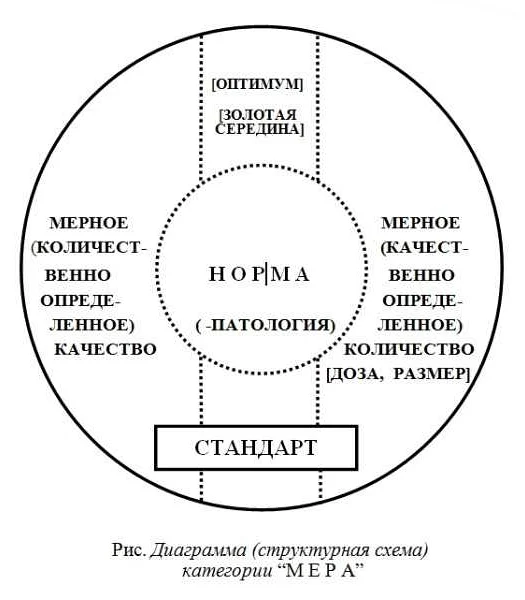
Когда применяется золотая середина, находится точка или значение, которое наиболее близко к центру между двумя экстремальными значениями. Это значение может быть определено посредством различных методов, таких как формулы, алгоритмы или даже эмпирический анализ.

Принцип золотой середины часто используется в различных областях математики, таких как оптимизация, теория вероятностей, статистика и другие. Он помогает найти оптимальное решение, которое в некотором смысле «находится посередине» между двумя крайностями.

Примерами применения золотой середины в математике могут быть поиск оптимальной точки на графике функции, разделение отрезка на две равные части, определение среднего значения из набора чисел и многое другое. В каждом случае золотая середина позволяет найти оптимальное или балансирующее значение.

Видео по теме:

Определение и примеры

Примерами применения золотой середины в математике могут служить следующие ситуации:

ПримерОписание

Определение оптимального размера	При выборе размера объекта, например, шрифта или изображения, необходимо найти такой размер, который не будет слишком маленьким, чтобы стать нечитаемым или незаметным, и не будет слишком большим, чтобы занимать слишком много места или привлекать слишком много внимания.
Определение оптимального времени	При планировании задач или распределении времени, необходимо найти такое время, которое не будет слишком коротким, чтобы не успеть выполнить работу, и не будет слишком длинным, чтобы не тратить ресурсы на незначительные задачи.
Определение оптимального значения	При нахождении оптимального значения в функции или уравнении, необходимо найти такое значение переменной, которое будет близким как к минимальному, так и к максимальному значению, чтобы достичь оптимального результата.

Применение золотой середины в математике позволяет достичь баланса и оптимальности в различных ситуациях, где требуется выбрать оптимальное значение или решение.

Принцип золотой середины в математике

В контексте оптимизации функций, принцип золотой середины заключается в нахождении такого значения переменной, при котором функция достигает минимума или максимума. Для этого проводится серия итераций, в течение которых выбираются две точки и вычисляется значение функции в этих точках. Затем выбирается новый интервал, содержащий «золотую середину» первого интервала, и процесс повторяется до достижения оптимального значения.

Примером использования принципа золотой середины может быть задача о нахождении минимальной или максимальной точки на графике функции. Для этого используется идея деления интервала на две части в определенной пропорции, где «золотая середина» является оптимальным значением.

Принцип золотой середины является одним из методов оптимизации, который широко применяется в математике и других науках. Он позволяет найти оптимальное значение в заданных рамках и достичь баланса между двумя крайностями.

Вопрос-ответ:

Что такое «золотая середина» в математике?

В математике «золотая середина» — это понятие, которое описывает ситуацию, когда есть определенное значение или диапазон значений, которые являются оптимальными или наиболее эффективными с точки зрения достижения желаемого результата.

Какие примеры есть «золотой середины» в математике?

Примеры «золотой середины» в математике включают в себя такие понятия, как оптимальная скорость при движении на автомобиле, оптимальное количество учебных часов для достижения максимальной успеваемости, оптимальное количество ресурсов для достижения максимальной производительности и т.д.

Как можно найти «золотую середину» в математике?

Для нахождения «золотой середины» в математике необходимо проанализировать цель или задачу и определить, какие значения или диапазоны значений будут оптимальными или наиболее эффективными. Это может включать в себя использование математических моделей, экспериментов или статистического анализа.

Какие факторы нужно учитывать при поиске «золотой середины» в математике?

При поиске «золотой середины» в математике нужно учитывать цель или задачу, ограничения, ресурсы, условия и другие факторы, которые могут влиять на оптимальные значения или диапазоны значений. Также важно учитывать, что «золотая середина» может быть относительной и может различаться в зависимости от контекста и конкретной ситуации.

Примеры применения золотой середины в математике

ПримерОбласть применения

Оптимизация функций	Метод золотого сечения широко используется для оптимизации функций в численных методах. Он позволяет находить экстремумы функций, минимизируя количество итераций.
Построение фракталов	Золотое сечение применяется при создании фракталов, таких как фрактал Фибоначчи или фракталы Жюлиа. Оно используется для определения пропорций и размеров фрактальных элементов.
Ряды Фибоначчи	Золотая середина связана с рядами Фибоначчи, где каждое число является суммой двух предыдущих чисел. Отношение двух последовательных чисел в ряде Фибоначчи приближается к золотому сечению.

Это лишь некоторые примеры применения золотой середины в математике. Она является мощным инструментом, который позволяет находить баланс и оптимальные значения в различных задачах и областях.

Золотая середина в математике и гармоническое среднее

Одним из примеров использования золотой середины в математике является определение гармонического среднего. Гармоническое среднее двух положительных чисел a и b определяется как обратное арифметическому среднему их обратных величин:

$$H = \frac{2}{\frac{1}{a} + \frac{1}{b}}$$

Гармоническое среднее используется, когда требуется найти среднее значение, учитывающее пропорциональное влияние обоих чисел. Оно часто применяется в задачах, связанных с обработкой данных и статистикой.

Например, если нужно найти среднюю скорость движения объекта, проведя два различных измерения, гармоническое среднее позволяет учесть их пропорциональное влияние. Таким образом, гармоническое среднее позволяет найти более точное среднее значение, учитывая особенности исходных данных.

Использование концепции золотой середины и гармонического среднего в математике позволяет находить оптимальные значения и принимать более точные решения в различных областях науки и техники.

Применение золотой середины в оптимизации функций

Применение золотой середины в оптимизации функций позволяет найти минимум или максимум функции на заданном интервале. Метод заключается в последовательном делении интервала на две части и выборе нового интервала в соответствии с золотым сечением. Процесс повторяется до достижения заданной точности или заданного числа итераций.

Преимуществом использования золотой середины в оптимизации функций является его эффективность и точность. Метод позволяет быстро находить оптимальное значение функции, особенно при работе с функциями, которые имеют один ярко выраженный экстремум.

Примером применения золотой середины может быть оптимизация функции в задачах поиска экстремумов в математическом моделировании или в задачах оптимизации в экономике. Например, при определении оптимального объема производства или при оптимизации распределения ресурсов.

Золотое сечение в геометрии и примеры его использования

В геометрии золотое сечение проявляется в специальных пропорциях, которые считаются эстетически приятными и гармоничными. Одно из наиболее известных применений золотого сечения в геометрии — это золотой прямоугольник, который имеет следующие свойства:

• Отношение длины большей стороны к меньшей стороне равно золотому сечению.
• Если отрезать квадрат, равный меньшей стороне, от данного прямоугольника, то оставшаяся фигура будет иметь такое же пропорциональное отношение сторон.
• Если продолжить деление на квадраты, то полученные фигуры будут иметь аналогичные пропорции.

Еще один пример использования золотого сечения в геометрии — это золотой треугольник. Он имеет следующие свойства:

• Отношение длины большей стороны к меньшей стороне равно золотому сечению.
• Если провести отрезок, соединяющий вершину треугольника с серединой противоположной стороны, он будет делиться в соответствии с золотым сечением.
• Также, если провести диагонали треугольника, они будут делиться в соответствии с золотым сечением.

Золотое сечение в геометрии используется для создания эстетических и гармоничных форм, а также для создания баланса и пропорций в различных изображениях, архитектуре и дизайне.

Золотое сечение в числовых рядах и его значения

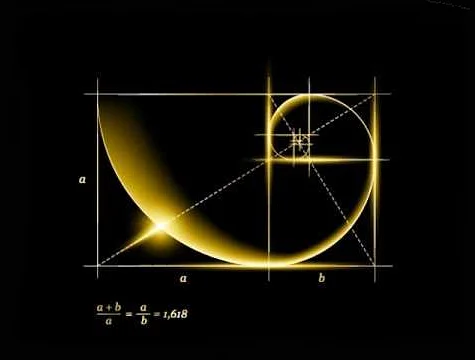
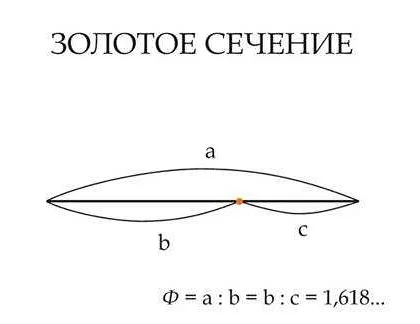
Золотое сечение в числовых рядах возникает при делении отрезка на две неравные части таким образом, что отношение длины всего отрезка к большей части равно отношению большей части к меньшей части. То есть, если обозначить длину всего отрезка как a и длину большей части как b, то выполняется следующее равенство: a/b = (a+b)/a = φ.

Золотое сечение имеет множество интересных свойств и применений. Оно встречается в фракталах, гармоническом ряде, ряде Фибоначчи и многих других числовых рядах. Значения золотого сечения используются в архитектуре, живописи, музыке и дизайне, чтобы создать гармоничные и пропорциональные формы и композиции.

Примеры числовых рядов, содержащих золотое сечение, включают следующие:

Числовой рядЗначение золотого сечения

Ряд Фибоначчи	1.6180339887
Ряд гармонических чисел	1.6180339887
Ряд Люкаса	1.6180339887

Эти примеры демонстрируют, что золотое сечение является универсальной константой, которая повторяется в различных числовых рядах. Это позволяет использовать его для исследования и анализа различных математических и физических явлений, а также для создания красивых и гармоничных произведений искусства.