Золотое число в математике: что это такое и как оно применяется

Золотое число — это математическая константа, которая является решением квадратного уравнения. Оно имеет множество интересных свойств и широкое применение в науке и искусстве. Узнайте, как определить золотое число и как оно связано с золотым сечением.

В математике есть множество интересных констант и число φ, или золотое число, является одним из наиболее загадочных и уникальных.

Золотое число обычно обозначается буквой φ и равно примерно 1.61803398875. Оно было открыто в древности греками и связано с пропорцией золотого сечения. Эта пропорция проявляется во многих важных аспектах жизни, включая искусство, архитектуру и дизайн, а также в научных открытиях и технологиях.

Узнать золотое число можно с помощью формулы: φ = (1 + √5) / 2. Одной из забавных особенностей φ является то, что оно является иррациональным числом, которое не может быть выражено в виде обыкновенной дроби, что делает его бессмысленным для округления.

Золотое число имеет широкий спектр применения в науке и технологиях, таких как компьютерное моделирование, финансовая аналитика, анализ изображений и обработка данных, а также в криптографии и методах защиты информации.

Золотое число в математике

Золотое число — это особое число, которое обозначается символом φ (фи). Оно является иррациональным числом и равно примерно 1,6180339887…

Золотое число имеет свойства, которые делают его интересным в математике и в других областях науки и искусства. Например, если разделить линию на две части таким образом, чтобы отношение длины большей части к меньшей было равно φ, то такое деление называется «золотым разрезом» и считается особенно эстетичным.

Формула для вычисления золотого числа выглядит так:

φ = (1 + √5) / 2

Золотое число широко используется в финансовой математике, геометрии, в науке о материалах и в других областях. Оно также встречается во многих произведениях искусства, от архитектуры до живописи.

• Применение золотого числа в архитектуре: многие здания, от древних греческих храмов до современных небоскребов, были построены с применением золотого разреза
• Применение золотого числа в искусстве: золотой разрез может использоваться для создания «золотых сечений» на картинах или в фотографии
• Применение золотого числа в музыке: некоторые музыканты используют золотое число для создания музыкальных пропорций и гармоний

Видео по теме:

Определение золотого числа

Золотое число (фи) в математике является пропорцией между двумя отрезками, такими, что более длинный отрезок делится пропорционально наибольшему и наименьшему из них. При этом отношение большего отрезка ко всей линии равно отношению меньшего отрезка к большему. Математически золотое число обозначается греческой буквой φ (фи) и равно приблизительно 1,618033988749895.

Золотое число является иррациональным числом, что означает, что оно не может быть представлено в виде дроби и не имеет периодической десятичной записи. Оно не имеет конечного или повторяющегося десятичного разложения.

Золотое число было изучено еще в Древней Греции и использовалось в искусстве и архитектуре, так как его пропорции были считаемыми идеальными и приятными для глаза. Сегодня золотое число используется в математике, физике, биологии и других науках. Это число обладает некоторыми удивительными математическими свойствами и широко применяется в геометрии, теории чисел, теории вероятности и других областях математики.

Золотое число также применяется в финансовой аналитике, при расчете кредитов, физических свойств комнат и зданий, а также в различных инженерных областях, таких как устойчивость структур и технологии изготовления.

История открытия золотого числа

Золотое число является одним из самых известных математических констант. Его значение приблизительно равно 1,6180339887… Это число получило свое название из-за его свойств во многих областях науки и искусства: золотой пропорции, золотых отношений и т.д.

Первые упоминания о золотом числе появились у древнегреческих философов, таких как Пифагор, Фидий и Эвклид. Они обнаружили, что золотое число может быть найдено путем деления линии на две части, таким образом, чтобы отношение длины целой линии ко всей длине, равной сумме двух частей, было таким же, как отношение более длинной части к более короткой. Затем Аристотель использовал это отношение для определения золотых пропорций в архитектуре и искусстве. Он также заметил, что золотое число может быть найдено путем решения квадратного уравнения с единичным корнем.

Сначала золотое число было формально определено в XIII веке Фибоначчи, который заметил, что различные элементы в его последовательности чисел Фибоначчи стремятся к золотому числу в пределе. Затем в XVI веке немецкий математик Лукас Пачольли создал термин «золотое сечение», чтобы описать эту константу.

В настоящее время золотое число является важным элементом в различных областях науки, таких как генетика, криптография, экономика и т.д. Оно также используется в различных формах искусства, включая архитектуру, живопись, музыку, фотографию и т.д.

Как вычислить золотое число

Золотое число, также известное как золотое сечение, можно вычислить несколькими способами:

1. Решением квадратного уравнения x^2=x+1;
2. Формулой Фибоначчи;
3. Приближенным методом с помощью серии дробей Египетских ученых.

Первый способ дает точное значение золотого числа, которое равно (1 + √5) / 2 или примерно 1,6180339887. Остальные способы дают лишь приближенные значения.

С помощью формулы Фибоначчи золотое число можно выразить как отношение двух последовательных чисел Фибоначчи, например, F(n) / F(n-1), где F(n) — n-ое число Фибоначчи. Чем больше значения n, тем точнее полученное значение золотого числа.

Приближенный метод с помощью серии дробей Египетских ученых заключается в последовательном нахождении максимальных целых чисел, которые дают дробное значение меньшее, чем золотое число. На каждой итерации получается дробь вида 1 / (a + b), где a и b — уже найденные максимальные целые числа. Последовательность дробей уже известна и записана в таблицах Евклида.

Свойства золотого числа

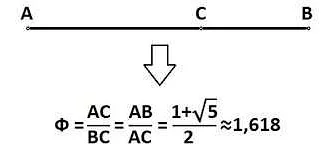
Соотношение между отрезками

Золотое число обладает уникальным свойством соотношения между отрезками. Если разделить отрезок на две части так, чтобы более короткая часть относилась к длинной, как вся относится к большей, то это отношение равно примерно 0.618. Таким образом, пропорции золотого числа могут быть обозначены как 1:0,618 (или 0,618:1, если рассматривать отношение наоборот).

Связь с Фибоначчи

Золотое число имеет тесную связь с последовательностью Фибоначчи. Каждый последующий член последовательности Фибоначчи является суммой двух предыдущих, начиная с 1 и 1. Когда эти числа начинают делить друг друга, приближаясь к золотому числу, отношение каждой пары чисел приближается к 1.618.

Присутствие в природе

Золотое число имеет множество приложений в природе. Например, отношения между размерами тела ряда живых организмов соответствуют золотому сечению: соотношение длины тела к ширине головы у птиц, соотношение длины лепестков многих цветов, расстояние от центра спирали раковин моллюсков и т. д.

Использование в искусстве и архитектуре

Золотое число и его свойства также нашли применение в искусстве и архитектуре. Расположение элементов на картинах и фотографиях, форма и расположение окон и дверей в зданиях, высота и ширина фигур, созданных в скульптуре и т. д., может быть определена с использованием золотого числа и соотношениями пропорций, которые оно определяет.

Таблица значений золотого числаЗначениеДесятичное приближение

Φ	1,618033988749895
1/Φ	0,6180339887498948

Золотое сечение

Золотое сечение — это математический термин, означающий деление отрезка на две части таким образом, чтобы соотношение длин большей и меньшей частей было равно отношению длины всего отрезка к длине большей части.

Часто это соотношение выражается в числовом виде как 1.618, а его математическое обозначение — символ φ (фи).

Золотое сечение имеет множество математических и философских применений, оно используется в архитектуре и дизайне, в искусстве и музыке. Например, золотое сечение часто используется для создания гармоничной композиции в изображениях и для определения пропорций в архитектурных сооружениях.

Также золотое сечение применяется в финансовых расчетах и торговле на финансовых рынках. В этом случае концепция золотого сечения используется для определения уровней поддержки и сопротивления и для прогнозирования изменений цен на рынке.

Интересно, что золотое сечение не является уникальной математической константой. Есть сходные константы, такие как число Сильвестра и число Эйлера, которые также обладают некоторыми свойствами золотого сечения.

Золотой прямоугольник

Золотой прямоугольник – это такой прямоугольник, у которого соотношение длины бóльшей стороны к длине меньшей стороны равно золотому сечению. В математике золотое сечение – это иррациональное число, равное (1+√5)/2 или приблизительно 1.61803398875.

Золотой прямоугольник часто встречается в природе и в искусстве, и считается наиболее эстетичным из всех пропорций. Например, форма лепестков цветов, раковины улиток и моллюсков, а также архитектурные проекты знаменитых строителей как Андреа Палладио и Леонардо да Винчи, основаны на золотом прямоугольнике.

Некоторые считают, что золотой прямоугольник имеет психологическое воздействие на человека и может вызывать чувство удовлетворения и гармонии. В связи с этим, золотой прямоугольник используется в дизайне, рекламе и веб-разработке, например, для создания гармоничного и удобочитаемого макета веб-страницы.

Для создания пропорций золотого прямоугольника используются различные математические формулы, например, можно вычислить коэффициент золотого сечения, используя формулу из Фибоначчиевой последовательности.

Золотая спираль

Золотая спираль – это спираль, которая основана на числе Фибоначчи и золотом сечении. Она получается, если провести дуги окружностей, у которых радиус соответствует числам Фибоначчи. Их центры лежат на главной диагонали квадрата, который имеет сторону равную числу Фибоначчи.

Такая спираль является одним из примеров фракталов, а также визуальным проявлением золотого сечения, которое является гармоничной пропорцией в природе и искусстве. Золотая спираль можно увидеть во многих объектах, например, в морских раковинах, цветках подсолнуха, форме галактик и гребешках.

Кроме того, золотая спираль используется в дизайне и компьютерной графике. Её применяют для создания более гармоничного и привлекательного дизайна, а также для расположения элементов на странице.

В целом, золотая спираль является интересным математическим объектом, который не только имеет эстетическое значение, но и находит применение в различных областях, от искусства до дизайна и науки.

Золотой угол

Золотой угол — это угол, который делит отрезок на две неравные части таким образом, что отношение большей части к меньшей равно золотому сечению, которое обозначается буквой φ (фи). Значение золотого сечения составляет примерно 1,6180339887 и является иррациональным числом.

Золотой угол является основным элементом золотой пропорции, которая широко применяется в архитектуре, дизайне, живописи, музыке и других областях.

Чтобы вычислить значение золотого угла, можно воспользоваться следующей формулой: φ = (1 + √5) / 2 ≈ 1,6180339887.

Золотой угол имеет много свойств и применений, например:

• Он является наиболее эстетически приятным углом для человеческого глаза, что делает его популярным в искусстве и дизайне.
• Его можно использовать как универсальный масштаб для создания пропорций в различных объектах, таких как скульптуры, здания и мебель.
• Он является ключевым элементом в теории музыки, где золотое сечение используется для определения гармонических отношений в музыкальных произведениях.

В целом, золотое число и золотой угол имеют широкие и разнообразные применения в различных областях знания, и продолжают привлекать внимание ученых и искусствоведов со всего мира.

Применение золотого числа в искусстве

Золотое число (1,618 …), также известное как Фи или Золотое сечение, было использовано в искусстве уже много лет. Использование этого числа позволяет художникам создавать произведения, которые не только красивы, но и приятны для глаза.

Одним из примеров использования золотого числа в искусстве является создание идеальных пропорций в картинах. Картины, созданные с использованием золотого числа, выглядят более сбалансированными и привлекательными для зрителя.

Кроме того, золотое число также используется в создании форм скульптур. Когда скульпторы используют золотое число в процессе создания своих произведений, они могут создавать красивые и эстетически приятные объекты искусства.

Золотое число также может быть использовано в дизайне интерьера, создании ландшафтов и даже одежды. Использование Фи может помочь дизайнерам создавать сбалансированные и привлекательные образы.

Наконец, золотое число часто используется в фотографии и графическом дизайне для создания привлекательных и эстетически приятных композиций.

В искусстве золотое число является мощным инструментом, который позволяет художникам и дизайнерам создавать произведения, которые не только красивы, но и приятны для глаза. Использование Фи позволяет добиться сбалансированности и гармонии в работах, что делает их более привлекательными для зрителя.

Применение золотого числа в архитектуре

Золотое число – это математический принцип, используемый в архитектуре для создания баланса и гармонии в форме и пропорциях зданий. Это число определяется как отношение двух отрезков таким образом, что более длинный отрезок делится на меньший так, чтобы соотношение между ними было одинаковым, как между большим отрезком и всей его длиной.

Золотое число имеет множество применений в архитектуре, от пропорций фасадов до формы колонн и пространств внутри зданий. Необычайно гармонично выглядит здание, выполненное в соотношении 1:1,618. Такое соотношение используется для определения пропорций между окнами, дверьми, ступенями лестниц и других элементов зданий.

Также золотое число позволяет создать правильную форму колонн, учитывая пропорции их диаметра и высоты. Внутренние пространства зданий тоже могут быть построены с использованием золотого числа, что создает ощущение равновесия и прозрачности архитектурной композиции.

Таким образом, применение золотого числа в архитектуре – это не только способ создания эстетической и гармоничной формы здания, но и математически обоснованный метод оптимизации пространства и пропорций.

Применение золотого числа в науке и технике

Золотое число (φ) является математическим символом бесконечности, который широко используется в науке и технике. Формула золотого числа определяется как (1+квадратный корень из пяти) разделенное на два.

Золотое число используется для создания гармоничных дизайнов и геометрических форм. Оно является идеальным соотношением, создающим пропорциональные и привлекательные формы в природе, таких, как фракталы и кристаллы.

В архитектуре золотое число используется для расчета пропорций зданий, создания красивых фасадов и определения местоположения окон и дверей. Оно также используется в музыке и искусстве для создания гармоничных мелодий и композиций.

Золотое число также используется в финансовой математике, где его применяют для расчета расходов и доходов при инвестировании. Кроме того, оно используется в компьютерных науках при разработке алгоритмов и при анализе данных.

В природе золотое число также присутствует в математических законах, описывающих рост и распределение растений, а также в форме раковины улитки и лепестков цветов. Оно также встречается в математических моделях, использующихся для анализа климата и популяций животных.

В целом, золотое число имеет широкое применение в различных областях науки и техники. Оно является ключом к созданию гармоничных форм и пропорций в природе, искусстве и архитектуре, а также является важным инструментом в финансовой и компьютерной математике.

Вопрос-ответ:

Что такое золотое число в математике?

Золотое число – это иррациональная математическая константа, обозначаемая буквой φ («фи»). Фи равняется приблизительно 1,618033988749894. Оно имеет свойства и особенности, которые делают его интересным в различных областях математики, физики, искусства и технологий.

Как вычислить золотое число?

Золотое число может быть вычислено различными способами, но один из наиболее простых – это решить квадратное уравнение x²-x-1=0, которое имеет два корня: (1+√5)/2 и (1-√5)/2. Первый корень – это золотое число. Также можно использовать формулу φ = (1+√5)/2 для вычисления.

Какое применение имеет золотое число в математике?

Золотое число широко используется в математике. Оно становится ключом к пониманию ряда чисел Фибоначчи, кристаллических структур, фрактальной геометрии, теории чисел, теории вероятности и других областей. Золотое число также используется в частотных преобразованиях и в некоторых алгоритмах машинного обучения.

Есть ли связь между золотым числом и золотым сечением?

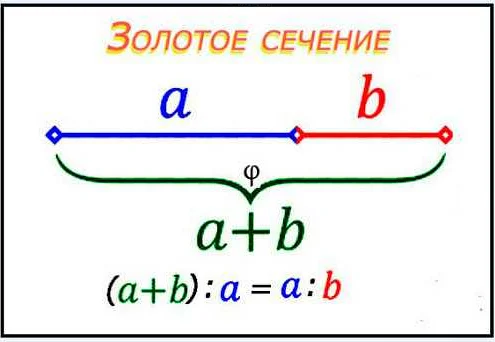
Да, золотое число и золотое сечение тесно связаны. Золотое число определяет золотое сечение – это пропорция, при которой более длинный сегмент разбит на две части с тем же отношением, что и меньший сегмент к большему. Это означает, что соотношение между a и b в золотом сечении равно φ = (a+b)/a = a/b = 1,618…

Как золотое число связано с числами Фибоначчи?

Числа Фибоначчи – это последовательность чисел, где каждое число является суммой двух предыдущих чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21 и т.д. Золотое число связано с числами Фибоначчи через их отношение – каждое последующее число Фибоначчи, начиная с третьего, делится на предыдущее число, и отношение этих чисел приблизительно равно золотому числу.

Какое влияние золотое число имеет на искусство и архитектуру?

Золотое число играет важную роль в искусстве и архитектуре. Оно используется для создания гармоничных пропорций и разделения пространства на визуально равные части. Золотое сечение можно обнаружить в произведениях искусства, таких как картины, скульптуры и архитектурные сооружения, включая здания и мосты.

Можно ли увидеть золотое число в природе?

Да, золотое число можно увидеть в природе. В некоторых живых организмах, таких как семена подсолнечника и ананаса, расположение лепестков соответствует золотому сечению. Кроме того, золотое сечение можно обнаружить в форме раковин некоторых морских животных, в облачениях и звездных системах, и в других природных объектах.