Что значит звездочка в математике

Звездочка в математике является символом умножения. Она используется для обозначения операции умножения чисел или переменных. Узнайте, как работает звездочка в математике и как она применяется в различных выражениях и уравнениях.

Звездочка – это один из наиболее распространенных символов, используемых в математике. Она обладает особой значимостью и имеет множество применений в различных областях науки. Звездочка часто используется для обозначения умножения, но также имеет другие интересные и важные математические значения.

В контексте умножения звездочка является одним из наиболее распространенных символов. В выражении «2 * 3» звездочка обозначает операцию умножения – перемножение двух чисел, чтобы получить их произведение. Например, «2 * 3 = 6». Звездочка также может использоваться в качестве знака умножения в алгебраических выражениях и уравнениях.

Однако звездочка имеет и другие значения в математике. Например, в теории вероятности звездочка используется для обозначения операции свертки, которая позволяет комбинировать две функции. В геометрии звездочка может использоваться для обозначения пересечения двух прямых линий или плоскостей. Также звездочка может обозначать комбинаторный символ – факториал, который используется для вычисления числа перестановок или сочетаний.

Звездочка – универсальный и многофункциональный символ в математике, который имеет различные значения и применения. Она используется для обозначения умножения, свертки, пересечения и факториала. Понимание этих значений поможет математикам и научным исследователям более глубоко понять и применять различные концепции и методы в своих исследованиях.

История возникновения звездочки

Изначально звездочка была символом множества и обозначала «существуют» или «существует». В древнем Египте звездочка использовалась для обозначения небесного светила и была символом божественной сущности.

В математике звездочка впервые появилась в XVIII веке благодаря английскому математику Томасу Бэйли.

С течением времени звездочка получила много разных значений и применений. В алгебре звездочка обозначает умножение, а в математической логике — логическое «И».

В программировании звездочка используется для обозначения указателей, а в регулярных выражениях — для обозначения любого символа.

Таким образом, звездочка является важным и многофункциональным символом в математике и других науках.

Значение звездочки в математике

Звездочка (*) в математике может иметь различные значения и применения в разных областях математических наук. Она используется в различных математических операциях, обозначениях и символах.

Одним из наиболее распространенных значений звездочки является символ умножения. В алгебре и арифметике звездочка используется для обозначения операции умножения двух чисел. Например, выражение 2 * 3 означает умножение числа 2 на число 3.

Звездочка также может использоваться для обозначения приведенной формы умножения. Например, выражение (a + b)*(c + d) означает умножение суммы a и b на сумму c и d.

В статистике звездочка может обозначать значимость и статистическую значимость. Она может использоваться в статистических таблицах для обозначения уровня значимости и статистической значимости результатов.

Звездочка также может обозначать произведение или сопряжение в контексте комплексных чисел. В теории чисел звездочка может использоваться для обозначения операции умножения в кольцах и алгебрах.

В математической нотации звездочка может быть использована для обозначения различных символов и переменных. Например, звездочка может использоваться для обозначения неизвестной переменной или неопределенного значения.

В общем, значение и применение звездочки в математике зависит от контекста, в котором она используется. Она может иметь различные значения в разных областях математических наук и служить для обозначения различных операций, символов и переменных.

Применение звездочки в научных исследованиях

Звездочка (*) в математике имеет много применений, и она также нашла свое место в научных исследованиях. В ряде научных статей можно встретить использование звездочки для обозначения значимости статистических результатов.

Звездочка используется для обозначения уровня значимости (p-value) в статистике. Уровень значимости показывает вероятность получения таких или более экстремальных результатов, если нулевая гипотеза верна. Если полученное значение p-value меньше установленного уровня значимости (обычно 0.05 или 0.01), то результат считается статистически значимым и обозначается одной или несколькими звездочками.

Например, если результат исследования показывает p-value меньше 0.05, то обычно используется одна звездочка (*) для обозначения статистической значимости. Если p-value меньше 0.01, то используется две звездочки (**), а если p-value меньше 0.001, то используется три звездочки (***).

Применение звездочки для обозначения статистической значимости помогает исследователям визуально выделить важные результаты и легко интерпретировать их. Это также помогает читателям научных статей быстро понять, насколько результаты исследования достоверны и могут быть приняты во внимание.

Уровень значимостиОбозначение звездочками

p-value < 0.05	*
p-value < 0.01	**
p-value < 0.001	***

Таким образом, звездочка в научных исследованиях играет важную роль в обозначении статистической значимости результатов и помогает исследователям и читателям лучше понять результаты исследований.

Звездочка в статистике

Звездочка (*) в статистике часто используется как символ, обозначающий значимость или статистическую значимость. Она может быть использована в различных контекстах и иметь разные значения.

Одним из наиболее распространенных случаев использования звездочки в статистике является обозначение уровня значимости. Уровень значимости показывает вероятность получить наблюдаемые данные, если нулевая гипотеза верна. Обычно используются следующие уровни значимости: 0,05 (*), 0,01 (**), 0,001 (***). Звездочки указывают на уровень значимости и позволяют судить о статистической значимости результатов.

Кроме того, звездочка может быть использована для обозначения выбросов или экстремальных значений в статистических данных. В этом случае звездочка указывает на наблюдения, которые сильно отличаются от остальных значений и могут оказывать влияние на результаты анализа.

Также звездочка может быть использована для обозначения пропущенных данных в статистической таблице. Например, если в таблице приведены данные только для некоторых групп или категорий, а данные для остальных групп отсутствуют, то звездочка может быть использована для обозначения пропусков.

Уровень значимостиОбозначение

0,05	*
0,01	**
0,001	***

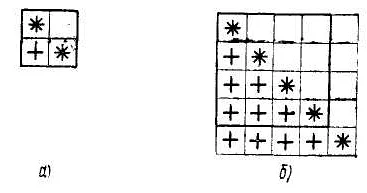
Звездочка в геометрии

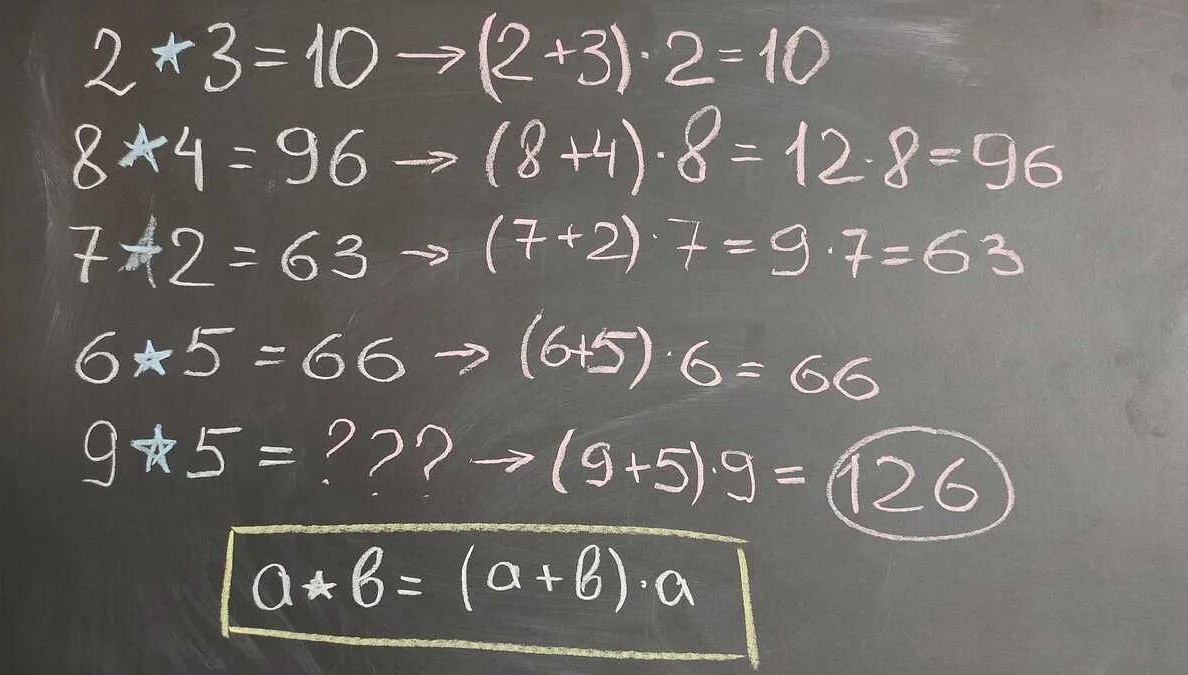
Эта геометрическая фигура имеет много интересных свойств и применений. Одно из основных применений звездочки в геометрии — это создание симметричных узоров и орнаментов. Благодаря своей симметрии, звездочка может использоваться для создания красивых и гармоничных узоров на различных поверхностях, таких как текстиль, ковры, украшения и т.д.

Звездочка также широко используется в геометрических расчетах и конструкциях. Она может быть использована для определения направления или выравнивания объектов, а также для нахождения определенных углов и длин сторон. Звездочка может быть полезной как в плоской геометрии, так и в трехмерном пространстве.

В геометрии звездочка может быть изображена и с помощью комбинации других геометрических фигур. Например, она может быть составлена из пересекающихся отрезков, окружностей или эллипсов. Такие комбинации позволяют создавать разнообразные формы и узоры, расширяя возможности использования звездочки в геометрии.

Использование звездочки в геометрии требует точности и внимательности, так как малейшее отклонение может привести к искажению формы или неправильным результатам. Поэтому при работе с звездочкой в геометрии необходимо придерживаться математических правил и методов для достижения точности и точных результатов.

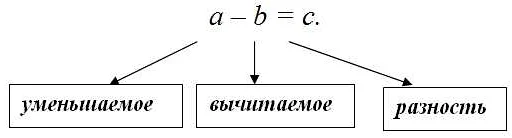
Звездочка в теории чисел

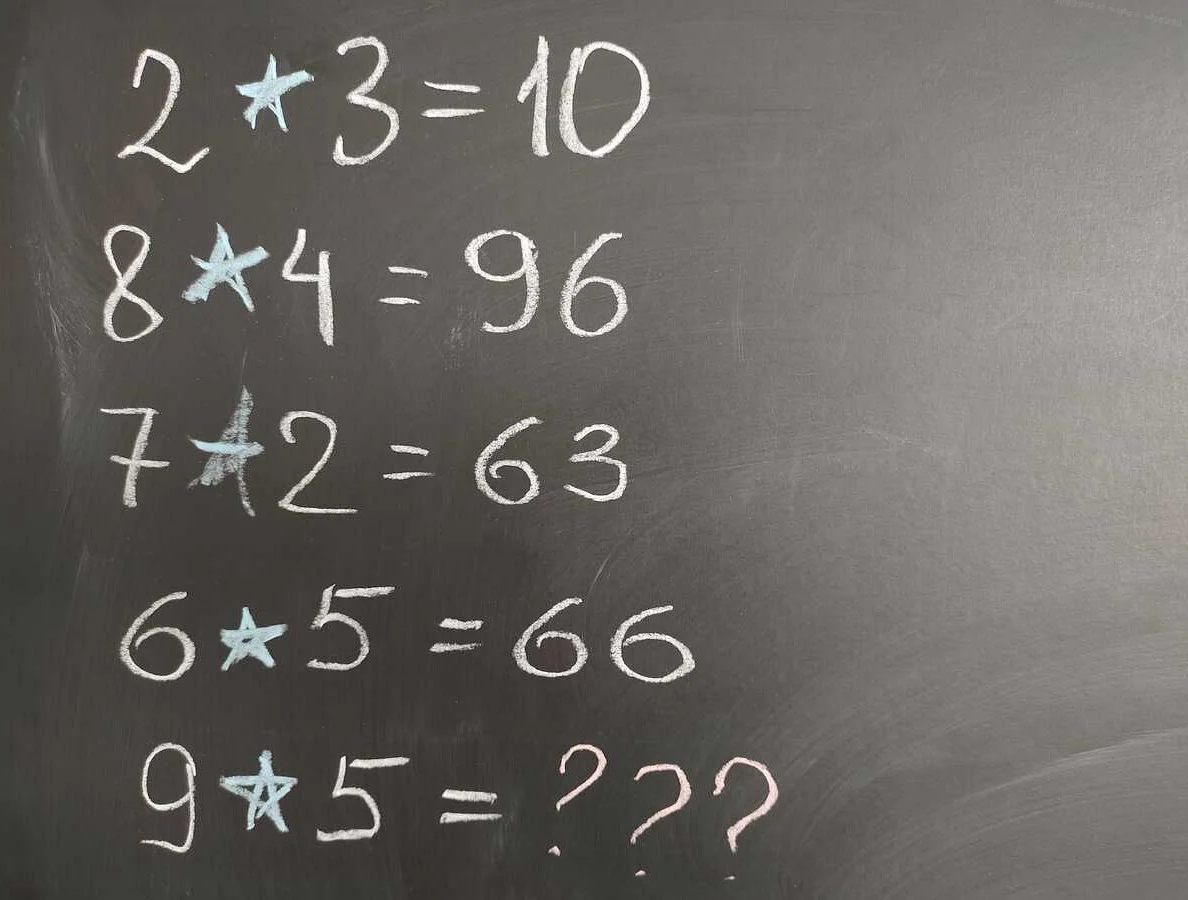
Звездочка (*) в теории чисел обозначает операцию умножения. Она используется для обозначения произведения двух чисел или переменных.

В теории чисел звездочка широко применяется для обозначения операции умножения, которая является одной из основных арифметических операций. Умножение двух чисел представляет собой операцию, при которой одно число (множитель) увеличивается в несколько раз в зависимости от значения другого числа (множителя).

Пример использования звездочки в теории чисел:

3 * 4 = 12

В этом примере звездочка (*) обозначает операцию умножения, а результатом операции является число 12. Первое число 3 является множителем, а второе число 4 — множителем.

Операция умножения имеет множество свойств, которые позволяют упростить вычисления и решать различные математические задачи. Знание и понимание этих свойств является важным для изучения и применения теории чисел.

Звездочка в теории графов

В случае звездочки граф состоит из одной центральной вершины и нескольких периферийных вершин, которые связаны только с центральной вершиной. Центральная вершина называется центром звездочки, а периферийные вершины – лепестками.

Звездочка в теории графов имеет множество применений. Она может использоваться для моделирования сетей передачи данных, где центральная вершина представляет центральный узел, а периферийные вершины – конечные узлы сети. Также звездочка может быть использована для анализа социальных сетей, где центральная вершина представляет лидера или главного актера, а периферийные вершины – его подчиненных или партнеров.

Вопрос-ответ:

Что такое звездочка в математике?

Звездочка в математике — это символ, который широко используется для обозначения различных математических операций и концепций. В зависимости от контекста, звездочка может означать умножение, дополнение, комбинацию и многое другое.

Какая роль звездочки в математике?

Звездочка имеет различные роли в математике в зависимости от контекста. Она может использоваться для обозначения умножения, дополнения, комбинации, альтернативного решения и т. д. Звездочка также может быть использована в математических выражениях для уточнения приоритета операций.

Как применяется звездочка в алгебре?

В алгебре звездочка часто используется для обозначения умножения. Например, выражение 2 * 3 означает умножение числа 2 на число 3. Звездочка может также использоваться для обозначения применения операции умножения к большему количеству чисел, например, 2 * 3 * 4 * 5. Она также может использоваться для обозначения дополнения, как в выражении Aᶜ.

Как звездочка используется в теории вероятностей?

В теории вероятностей звездочка часто используется для обозначения комбинации. Например, выражение C(n,k) обозначает количество комбинаций из n элементов по k элементов. Это можно записать как nCk или n choose k. Звездочка также может использоваться для обозначения независимых событий, например, P(A * B) означает вероятность наступления событий A и B одновременно.

Как звездочка используется в программировании?

В программировании звездочка имеет различные значения в зависимости от языка программирования. Например, в некоторых языках звездочка может использоваться для обозначения указателя на адрес памяти. Она также может использоваться для обозначения операции разыменования указателя или умножения в числовых выражениях. Звездочка также может использоваться для обозначения указателя на функцию или переменную в некоторых языках программирования.

Что такое звездочка в математике?

Звездочка в математике обозначает множество всех значений, которое может принимать переменная. Она используется для указания на все возможные решения уравнения или неравенства.

Какая роль у звездочки в математике?

Звездочка играет важную роль в математике, она помогает нам указать на все возможные решения уравнения или неравенства. Это позволяет нам получить полную картину решений и более точно описать множество значений переменной.

Звездочка в алгебре

В алгебре звездочка (*), также известная как оператор умножения, используется для обозначения умножения чисел или переменных.

Умножение с помощью звездочки можно записать следующим образом:

• Умножение чисел: a * b = c, где a и b — множители, а c — их произведение.
• Умножение переменных: x * y = z, где x и y — переменные, а z — их произведение.

Применение звездочки в алгебре особенно важно при работе с алгебраическими выражениями. Например, выражение (2x + 3) * 4 можно преобразовать следующим образом:

1. Умножаем каждый член выражения на 4: 2x * 4 + 3 * 4.
2. Выполняем умножение: 8x + 12.

Звездочка также используется в алгебре для обозначения операции умножения в матрицах. Произведение матриц A и B записывается как A * B.

Кроме того, звездочка может использоваться в алгебре для обозначения других операций, таких как возведение в степень или символическое умножение в программировании.

Видео по теме: