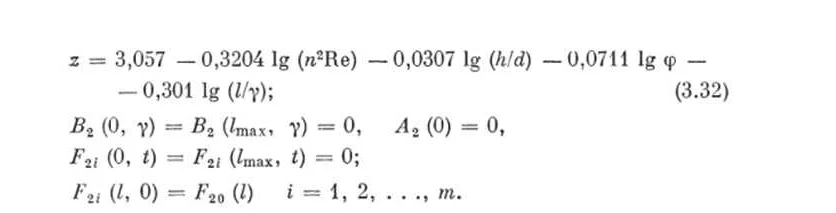Адекватность математической модели: понимание сущности и примеры применения

Адекватность математической модели – это способность описывать и предсказывать реальные процессы и явления с достаточной точностью. Подробности о том, что означает адекватность модели и как ее проверять, вы можете узнать из данной статьи.

Математическая модель – это способ описания системы при помощи математических символов и формул. Модели могут помочь в предсказании поведения системы и помочь в принятии решений. Однако, при построении математической модели возникает вопрос об адекватности – насколько точно она отражает реальные процессы. Если модель недостаточно адекватна, то результаты ее работы могут быть нерелевантными.

Например, одной из проблем моделирования является учет всех факторов, которые могут влиять на систему. Невозможно учесть каждую нюанс, и если какой-то фактор будет опущен, это может привести к неточным или неполным результатам. Кроме того, модель может быть изначально построена неправильно, и это также отразится на ее точности.

Существуют различные методы проверки адекватности модели, например, сравнение результатов моделирования с экспериментальными данными или проведение чувствительности модели к входным параметрам. Правильно выбранные методы могут помочь обнаружить ошибки в модели и улучшить ее точность.

Определение адекватности

Адекватность математической модели — это ее способность достаточно точно описывать явления, происходящие в реальности и использоваться для прогнозирования. Такой способностью обладают модели, которые находятся в достаточно близком соответствии с реальностью.

Если модель не является адекватной, она не может служить инструментом для научных исследований и использования в повседневной жизни. Фактически, применение неправильной модели может привести к незначительным ошибкам, а также к серьезным последствиям.

Существует несколько методов определения адекватности математической модели, которые можно применять в различных областях науки. Один из таких методов — проверка с помощью экспериментов, которые связаны с систематическим наблюдением и измерением реальных явлений. Это позволяет сравнить результаты, полученные от модели, с результатами, полученными непосредственно в реальности. Если результаты сопоставимы, то это говорит об адекватности модели.

Другим методом проверки адекватности является сравнение результатов, полученных с помощью различных моделей, с результатами наблюдений в реальном мире. Данный метод позволяет выбрать наилучшую модель, которая лучше всего описывает явления, происходящие в реальности.

Таким образом, определение адекватности математической модели является важной задачей в науке и практике. Надежность и качество модели является основными факторами для того, чтобы с ее помощью можно было получить точные прогнозы и достоверные результаты в исследованиях.

Примеры адекватных моделей

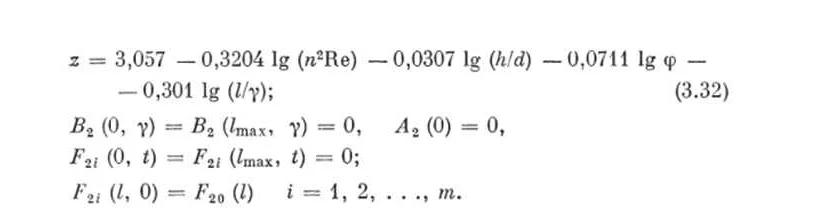
Модель Ньютона для движения тела

Модель Ньютона в математике является классическим примером адекватной модели. Она описывает движение тела с помощью формулы Ф = ма, где Ф — сила, м — масса тела, а — ускорение.

Модель Блэка-Шоулза для опционов

Модель Блэка-Шоулза используется для оценки цены опциона и определяет его «честную» стоимость. Она учитывает соотношение цены акции, стоимости страйк-опаса и времени до истечения опциона.

Модель SEIR для эпидемий

Модель SEIR (Susceptible-Exposed-Infected-Recovered) используется для описания динамики распространения эпидемических заболеваний. Она учитывает количество людей, которые могут заболеть, количество людей, уже зараженных, период заболевания и время исцеления.

Модель Фишера для денежного обращения

Модель Фишера используется для описания денежного обращения и учитывает влияние уровня инфляции на рост цен. Она учитывает количество денег в обращении, скорость обращения денег, уровень цен и объем товаров и услуг в экономике.

Модель Кобба-Дугласа для производительности

Модель Кобба-Дугласа описывает связь между входами (труд и капитал) и выходами (производственной мощностью) в производственном процессе. Она учитывает влияние производительности и технологических изменений на рост производства.

• Примеры адекватных моделей:
• Модель Ньютона для движения тела
• Модель Блэка-Шоулза для опционов
• Модель SEIR для эпидемий
• Модель Фишера для денежного обращения
• Модель Кобба-Дугласа для производительности

МодельОписание

Ньютона	Описывает движение тела
Блэка-Шоулза	Оценивает стоимость опциона
SEIR	Описывает динамику распространения эпидемий
Фишера	Описывает денежное обращение
Кобба-Дугласа	Описывает производительность

Примеры неадекватных моделей

Математические модели могут быть неадекватными в различных ситуациях. Рассмотрим некоторые примеры:

1. Модель среднего значения: очень часто используется модель, основанная на среднем значении для описания большого числа явлений. Однако, это может не работать для данных, которые имеют крайне несимметричное распределение.
2. Модели линейной регрессии с низким коэффициентом детерминации: модели линейной регрессии используются для прогнозирования зависимых переменных по независимым переменным. Коэффициент детерминации отражает долю изменчивости зависимой переменной, объясненную моделью. Однако, если коэффициент детерминации очень низкий, это может указывать на то, что модель неадекватна.
3. Модели на основе корреляции: корреляция между двумя переменными означает, что их значения связаны между собой. Однако, это не означает, что одна переменная причина изменения другой переменной. Поэтому модели на основе корреляции могут быть неадекватными при попытках выявить причинно-следственные отношения.

Таблица: Примеры неадекватных моделейМодельПричины неадекватности

Модель среднего значения	Несимметричное распределение данных
Модели линейной регрессии	Низкий коэффициент детерминации
Модели на основе корреляции	Невозможность выявить причинно-следственные отношения

Неправильная модель может привести к ошибочным выводам и ухудшению качества принимаемых решений. Проверка адекватности модели – важный этап в процессе построения моделей для анализа данных.

Методы проверки адекватности модели

Адекватность математической модели это степень соответствия модели реальности. Проверка адекватности модели это важный этап в разработке модели, поскольку нерадивое использование неадекватной модели может привести к ошибкам и неправильным выводам.

Существует несколько методов проверки адекватности модели:

• Проверка на выбросы: Этот метод связан с проверкой на наличие значений, которые сильно отличаются от других значений в выборке. Такие значения могут быть результатом ошибок в данных или же связаны с факторами, которые не были учтены в модели. Если выбросы оказывают значительное влияние на результаты модели, то это может указывать на то, что модель не является адекватной.
• Сравнение результатов модели со статистическими данными: Этот метод заключается в сравнении результатов модели с уже известными статистическими данными. Если результаты модели значительно отличаются от ожидаемых значений, то это может свидетельствовать о том, что модель не является адекватной.
• Кросс-валидация: Этот метод проверки адекватности модели предполагает разделение данных на обучающую и тестовую выборку. На обучающей выборке модель строится, а затем на тестовой выборке проверяются результаты модели. Если результаты на тестовой выборке отличаются от ожидаемых, то это может указывать на то, что модель не является адекватной.
• Графический анализ: Этот метод предполагает визуальное сравнение модели с данными. Если модель точно отображает данные, то линия, построенная по результатам модели, будет идти близко к точкам данных. Если модель не является адекватной, то линия будет сильно отклоняться от точек данных.

Проверка адекватности модели не является единственным методом, но она является важным этапом в разработке математических моделей и может помочь избежать ошибок и неправильных выводов.

Статистические методы

Как правило, математические модели не являются абсолютно точными, поэтому для оценки их адекватности применяются различные статистические методы.

Один из таких методов – анализ регрессии. Он позволяет определить, как сильно связаны между собой две переменные, и оценить коэффициенты уравнения, которое связывает эти переменные.

Также используются тесты на значимость, которые позволяют определить, насколько отклонение реальных данных от предсказаний модели случайно, а насколько значимо. Например, тест Стьюдента используется для проверки значимости различий между выборками.

Другим методом является анализ дисперсии, который оценивает степень разброса данных относительно математического ожидания. Этот метод может быть применен для определения значимости различий между несколькими выборками.

И наконец, статистические методы позволяют проводить проверку гипотезы о соответствии модели реальным данным. Например, при помощи t-теста можно оценить, насколько вероятность ошибки первого рода в выборке, полученной с помощью модели, меньше заданного уровня значимости.

Методы машинного обучения

Машинное обучение — это категория искусственного интеллекта, изучающая методы извлечения правил и закономерностей из больших объемов данных. Существует множество методов машинного обучения, которые используются для решения различных задач в различных областях, например:

• Обучение с учителем (Supervised Learning): в этом методе модель обучается на данных, где каждый пример имеет метку класса или значение. Цель состоит в том, чтобы научить модель предсказывать метки значений для новых данных.
• Обучение без учителя (Unsupervised Learning): это метод, в котором модель не получает явный ответ на входных данных. Вместо этого она выявляет скрытые закономерности и структуры в данных, такие как кластеризация, сокращение размерности и т.д.
• Обучение с подкреплением (Reinforcement Learning): это метод, который основан на принципе стимулирования. Агент обучается, принимая решения и получая награды или штрафы за свои действия.

Для обучения моделей машинного обучения необходимо иметь набор данных, который разбивается на обучающую и тестовую выборки. Модель обучается на обучающей выборке, а затем оценивается на тестовой выборке. Также важно обеспечить достаточную обобщающую способность модели, чтобы она могла работать с новыми данными, которые не были использованы в процессе обучения.

Методы машинного обучения широко используются в разных отраслях, в том числе в медицине, банковском деле, производстве и других сферах. Они помогают автоматизировать задачи прогнозирования, классификации, кластеризации и оптимизации, снижая вероятность ошибок и улучшая качество принимаемых решений.

Методы моделирования

Модель – упрощенное изображение реального объекта или процесса, представленное с помощью математических формул. В зависимости от того, какого рода систему мы хотим проанализировать, существуют различные методы моделирования, позволяющие нам получить представление о поведении системы.

Аналитическое моделирование – метод моделирования, основанный на использовании математических выражений для описания поведения системы. Применяется в случаях, когда система удовлетворяет определенным математическим законам.

Симуляционное моделирование – метод моделирования, использующий компьютерную программу для моделирования поведения системы. Позволяет исследовать систему в различных условиях, изменяя параметры модели и наблюдая за реакцией системы.

Эмпирическое моделирование – метод моделирования, основанный на экспериментальных данных. Используется в случаях, когда математических законов, описывающих систему, нет или система не может быть описана с помощью формул.

Моделирование на основе экспертных оценок – метод моделирования, использующий знания и опыт экспертов для описания состояния системы. Применяется в случаях, когда нет точных данных, необходимых для создания математической модели.

Важно понимать, что ни один метод моделирования не является лучшим или наилучшим для всех ситуаций. Выбор метода зависит от того, какую систему мы исследуем, какие у нас данные и как мы планируем использовать модель в дальнейшем.

Взаимосвязь между адекватностью модели и ее целевым приложением

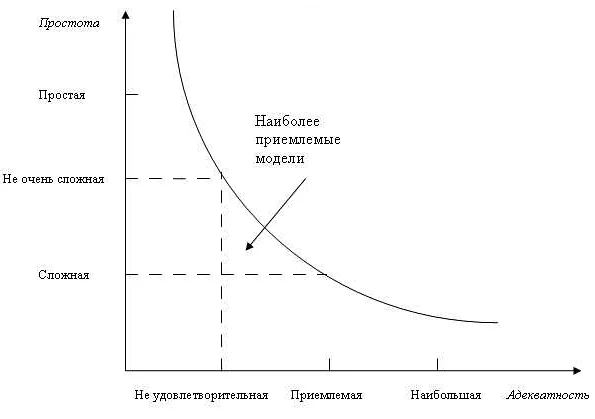
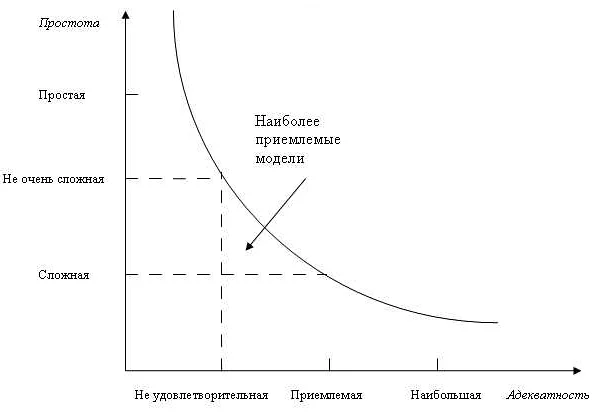
Адекватность математической модели является ключевым элементом ее использования в различных областях знаний. Она определяет, насколько точно модель отражает исследуемый процесс или явление. Однако, для того чтобы модель могла быть считаться адекватной, необходимо учитывать ее целевое приложение.

Целевое приложение модели определяется тем, для каких целей и задач была создана модель. Например, модель может использоваться для прогнозирования результатов эксперимента, определения оптимальных решений в различных ситуациях или для обучения студентов в учебном процессе. В каждом из этих случаев модель должна быть адекватной в соответствующем контексте.

Для того чтобы проверить адекватность модели в ее целевом приложении, необходимо использовать специальные методы проверки, которые позволяют сравнить результаты моделирования с реальными данными. Например, можно провести эксперимент или исследование на основе модели и сравнить полученные результаты с реальной ситуацией. Также есть специальные статистические методы, которые помогают оценить качество модели при ее применении в конкретной ситуации.

Таким образом, адекватность математической модели напрямую зависит от ее целевого приложения. Для каждой конкретной задачи необходимо выбирать соответствующую модель и проверять ее адекватность в соответствующем контексте. Только в этом случае можно быть уверенным в том, что модель будет полезна и даст необходимые результаты.

Видео по теме:

Вопрос-ответ:

Что такое адекватность математической модели?

Адекватность математической модели — это способность модели отображать реальный объект или явление с достаточной точностью и соответствием. Таким образом, адекватность модели означает, что она должна быть представлена в той форме, которая соответствует сущности объекта моделирования и обладает приемлемой степенью точности.

Какой пример может служить доказательством адекватности математической модели?

К примеру, успешное прогнозирование экономических показателей, таких как инфляция или рост ВВП при помощи эконометрических моделей. Если модель корректно отображает динамику изменения показателей в прошлом, то она, скорее всего, будет адекватна для прогнозирования в будущем.

Каковы причины недостаточной адекватности математической модели?

Причин недостаточной адекватности может быть несколько. Например, слишком простая модель может не учитывать все важные факторы, влияющие на рассматриваемое явление. Также неверно выбранные параметры или нехватка данных для определенных компонентов модели могут привести к ее недостаточной адекватности.

Влияет ли объем данных на адекватность математической модели?

Да, объем данных может влиять на адекватность математической модели. С одной стороны, чем больше данных используется в моделировании, тем более точной и адекватной будет модель. Однако, с другой стороны, некоторые модели могут оказаться чрезмерно сложными и перенасыщенными данными, что также влияет на их адекватность.

Может ли математическая модель быть слишком адекватной?

Да, математическая модель может быть слишком адекватной. Это может произойти, если модель была создана на основе исходных данных, которые не являются репрезентативными для всех возможных сценариев. В таком случае модель может оптимизироваться только для выборочных данных, что может привести к ее низкой способности к обобщению и низкой устойчивости при изменении входных данных.

Каковы последствия использования недостаточно адекватной математической модели?

При использовании недостаточно адекватной математической модели могут возникнуть серьезные последствия. Например, принятие неправильных решений на основе вычислений, полученных при помощи модели, может привести к значительным убыткам, как финансовым, так и техническим, в случае моделирования технических систем. Кроме того, использование недостаточно адекватной модели может привести к снижению доверия к самому методу математического моделирования.

Роль эксперимента в проверке адекватности

Математические модели используются в науке и инженерии для описания реальных систем и предсказания их поведения в различных условиях. Однако, невозможно создать математическую модель, которая бы полностью описывала реальное явление. Поэтому, важно проверять адекватность математической модели путем эксперимента.

Эксперимент является одним из ключевых методов проверки адекватности математических моделей. Он позволяет сравнивать результаты моделирования с фактическими данными, полученными в реальности. При этом, эксперимент должен быть тщательно спланирован и проведен, а полученные данные должны быть достоверными, чтобы результаты сравнения были корректными.

Результаты эксперимента могут использоваться для уточнения математической модели или ее парамтров. Если результаты эксперимента не соответствуют результатам моделирования, это может указывать на неправильность модели или ее параметров. В этом случае, математическая модель может быть улучшена путем изменения параметров или конструкции.

Таким образом, эксперимент играет важную роль в процессе проверки адекватности математических моделей. Он помогает уточнить модель и ее параметры, делая ее более точной и приближенной к реальности.

Применение адекватных моделей в реальных задачах

Адекватность математических моделей играет важную роль в решении реальных задач. Это так потому, что адекватная модель точно соответствует реальному явлению или процессу, что дает возможность точно прогнозировать его поведение и изменения.

Примером применения адекватной математической модели является прогнозирование погоды. На основе статистических данных и параметров погодного явления составляется математическая модель, которая позволяет точно прогнозировать погоду на несколько дней вперед.

Еще одним примером применения адекватной модели является проектирование автомобильных дорог. С помощью математической модели можно определить оптимальные параметры дороги, такие как ширина, радиус поворотов, уклон и другие. Это позволяет создать безопасные и комфортные условия для движения транспорта.

Для проверки адекватности математической модели используются различные методы, такие как анализ данных, эксперименты и сравнение результатов моделирования с реальными данными. Это позволяет установить точность и достоверность модели, что в свою очередь обеспечивает успешное решение реальных задач.

Таким образом, применение адекватной математической модели является необходимым условием в решении реальных задач в различных областях экономики, техники и науки.