Что такое число в математике определение

Число в математике — это абстрактное понятие, которое используется для описания количества, порядка, меры или отношения. Оно может быть представлено в различных формах, таких как натуральные числа, целые числа, рациональные числа, иррациональные числа и т. д. Числа являются основой для выполнения арифметических операций и решения математических задач.

Число – это одно из основных понятий математики, которое играет важную роль в научных исследованиях и повседневной жизни. Оно представляет собой абстрактную концепцию, которая используется для измерения, подсчета, описания и сравнения количественных характеристик различных объектов. Числа могут быть представлены различными способами, включая целые, дробные, рациональные и иррациональные числа.

В математике числа играют важнейшую роль и широко применяются для разработки теорий, моделей и алгоритмов. Они используются для изучения свойств и отношений между объектами, а также для решения различных задач. Например, числа используются для решения уравнений, предсказания результатов экспериментов, разработки криптографических систем, моделирования физических процессов и многого другого.

В математике числа являются основой всего ее аппарата и позволяют формализовать и описать различные явления и закономерности в мире. Они представляют собой не только средство для измерения и счета, но и абстрактную концепцию, которая позволяет нам понять и объяснить различные аспекты окружающего нас мира.

В заключении можно сказать, что число является фундаментальным понятием в математике, которое играет важную роль в научных исследованиях и практическом применении. Оно позволяет нам анализировать и описывать различные явления, предсказывать результаты и принимать важные решения. Без понимания и использования чисел мы были бы ограничены в наших возможностях в понимании мира и его законов.

Что такое число и как оно определяется

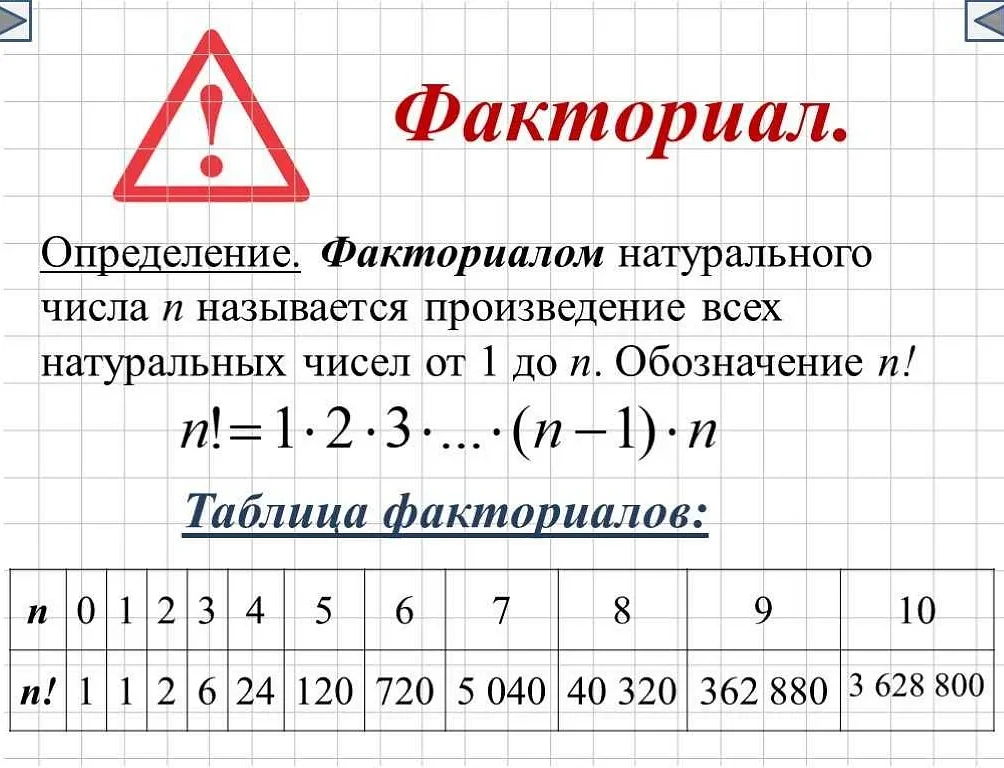
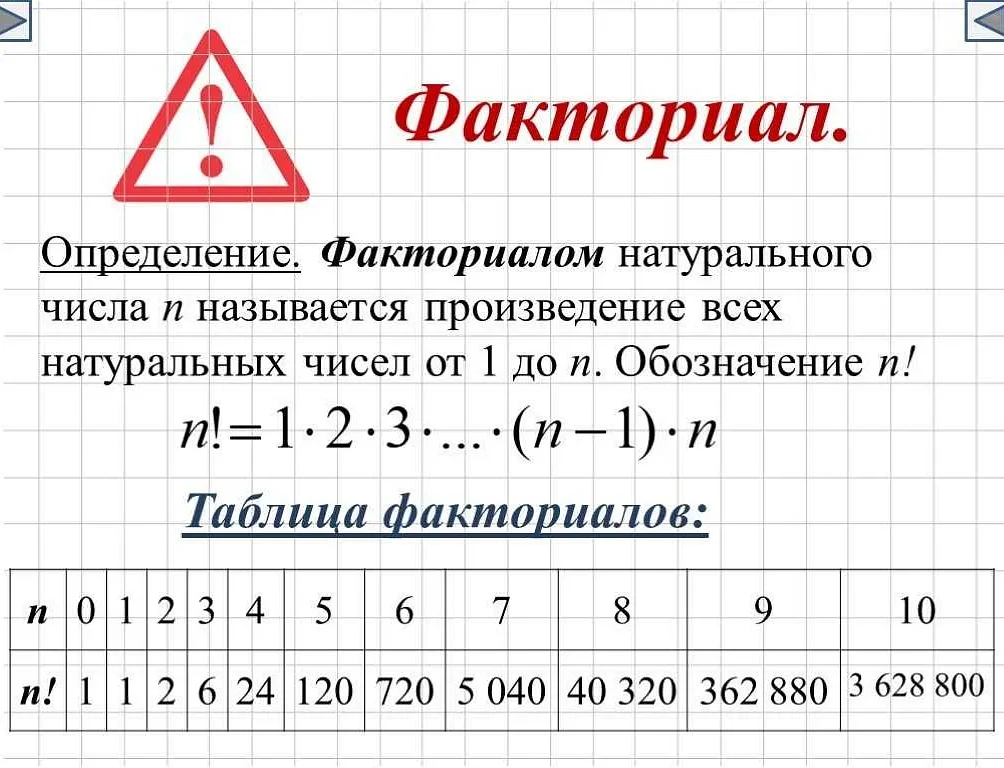
Определение числа — это процесс, который предписывает смысл и значения числовых символов. Оно основано на различных системах счисления, которые используются в разных культурах и областях знания.

Наиболее распространенная система счисления в современной математике — десятичная система счисления. В этой системе числа представлены десятью цифрами: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число может иметь различное количество цифр и разделителей в зависимости от своей величины и используемых математических операций.

Определение числа также включает его классификацию на различные типы, такие как натуральные числа, целые числа, рациональные числа и иррациональные числа. Натуральные числа — это положительные целые числа, которые используются для подсчета объектов. Целые числа включают в себя натуральные числа, а также их отрицательные значения и ноль. Рациональные числа — это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами. Иррациональные числа — это числа, которые не могут быть представлены в виде обыкновенной дроби и имеют бесконечное количество десятичных знаков без периода.

Определение числа также включает его свойства и операции, такие как сложение, вычитание, умножение и деление. Числа могут быть использованы для решения математических задач, моделирования физических явлений, анализа данных и многое другое. Они играют важную роль в науке, технике, экономике и других областях знания.

Роль чисел в математике и науке

В математике числа используются для выражения количественных отношений и связей между объектами. Они позволяют проводить точные расчеты, формулировать и доказывать теоремы, находить решения уравнений и разрабатывать новые математические модели и методы.

В науках числа также играют важную роль. Они используются для измерения физических величин, записи экспериментальных данных и описания закономерностей в природе. Например, в физике числа используются для определения скорости, массы, энергии и других физических параметров. В химии числа позволяют устанавливать соотношения между веществами и проводить точные расчеты реакций.

Без чисел просто невозможно развитие науки. Они являются основой для проведения экспериментов, формулирования гипотез и проверки теорий. Благодаря числам мы можем получать точные результаты, делать прогнозы, строить модели и принимать важные решения в научных исследованиях.

Важно отметить, что числа имеют не только количественное значение, но и символическое. Они могут представлять абстрактные понятия, отражать законы и закономерности, которые мы обнаруживаем в мире. Числа являются универсальным языком, который позволяет ученым общаться и обмениваться информацией.

Таким образом, роль чисел в математике и науке нельзя недооценивать. Они играют ключевую роль в процессе исследования, позволяют нам понять и объяснить мир вокруг нас, а также разрабатывать новые технологии и достижения в различных областях знания.

Различные типы чисел и их особенности

В математике существует несколько различных типов чисел, каждый из которых имеет свои особенности и применяется в определенных областях науки и жизни. Рассмотрим некоторые из них:

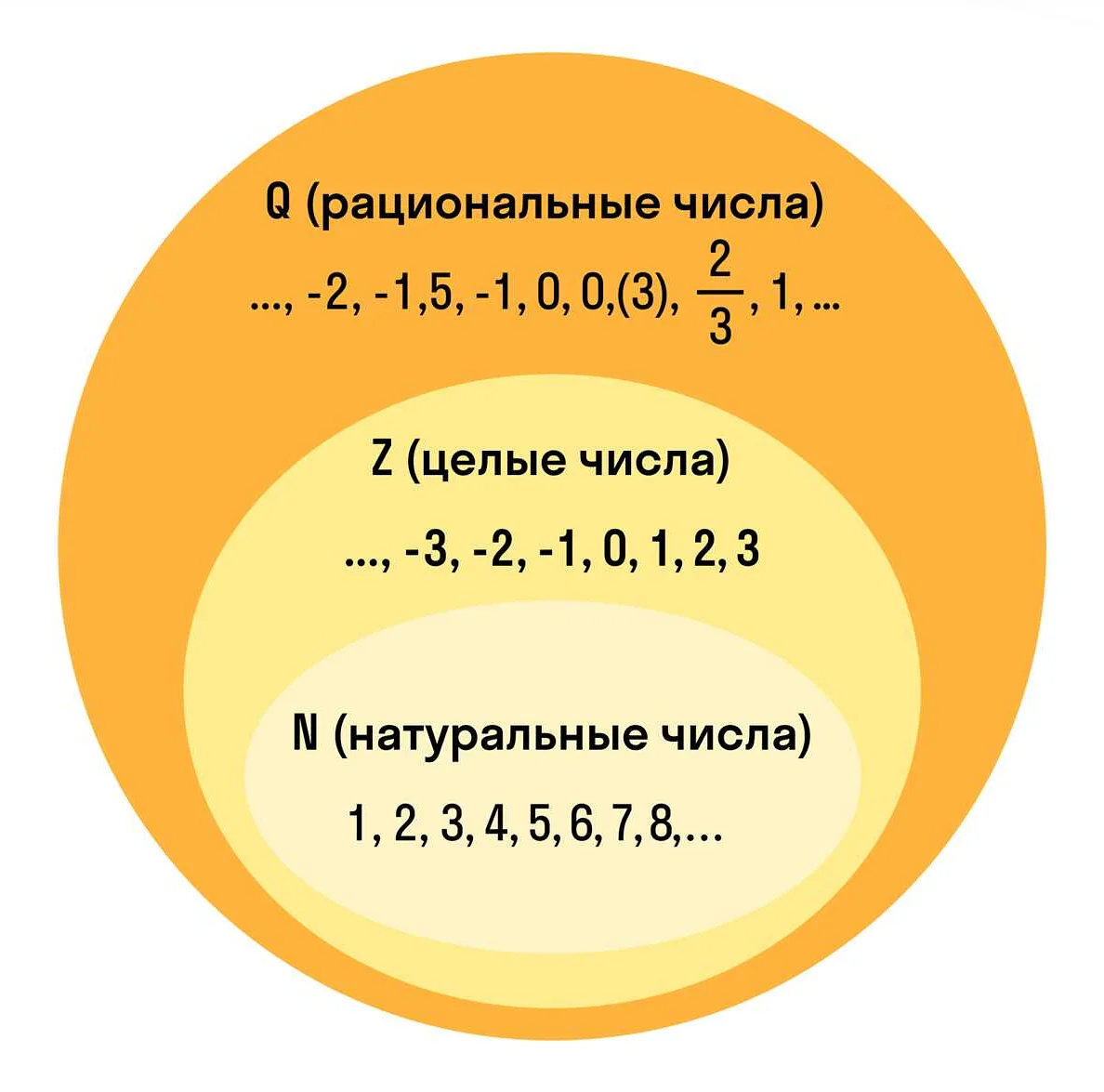
• Натуральные числа (N). Это числа, которые используются для подсчета элементов в конечных множествах. Они начинаются с единицы и не имеют верхней границы. Примеры: 1, 2, 3, 4, 5…
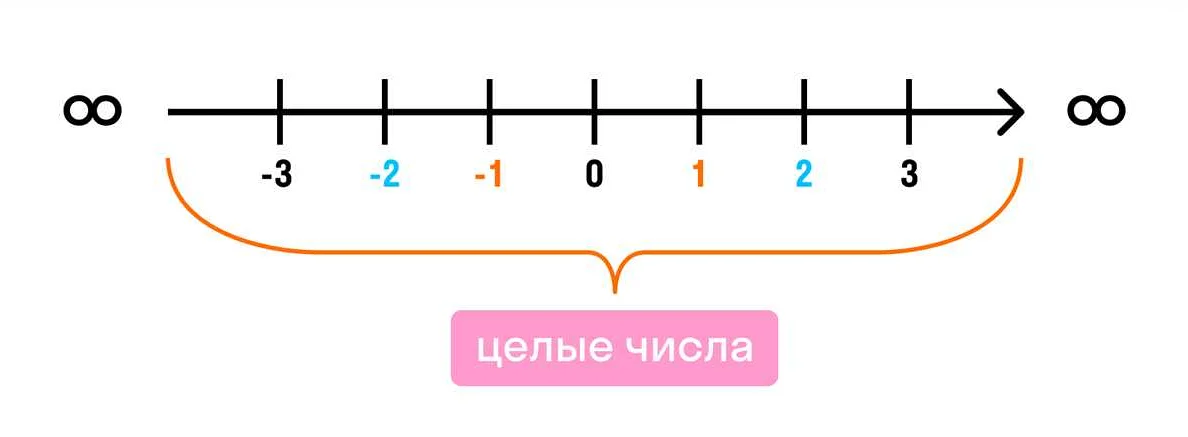
• Целые числа (Z). Это числа, которые включают натуральные числа, их противоположности (отрицательные числа) и ноль. Они используются для измерения долгов, температуры и других величин. Примеры: -3, -2, -1, 0, 1, 2, 3…
• Рациональные числа (Q). Это числа, которые могут быть представлены в виде дробей, где числитель и знаменатель являются целыми числами. Они используются для точного представления десятичных дробей и подсчета долей. Примеры: 1/2, 0.75, -3/4, 2/3…
• Вещественные числа (R). Это числа, которые могут быть представлены в виде десятичных дробей или бесконечных десятичных дробей. Они используются для измерения величин, которые могут быть представлены на числовой прямой. Примеры: 3.14, -0.5, 2.71828…
• Комплексные числа (C). Это числа, которые состоят из реальной и мнимой части. Они используются в математике и физике для решения уравнений и представления волн и сигналов. Примеры: 2 + 3i, -1 — 2i, 4i…

Каждый тип чисел имеет свои особенности и применяется в различных областях науки и жизни. Понимание этих различий помогает математикам и ученым применять числа в своих исследованиях и решать разнообразные задачи.

Числа и их применение в различных научных дисциплинах

В физике числа используются для измерения физических величин, таких как масса, скорость, температура и т.д. Например, при измерении массы объекта мы получаем числовое значение, которое позволяет сравнить его с другими объектами и сделать выводы о его свойствах и характеристиках.

В химии числа используются для выражения количества вещества, молекулярной массы, концентрации и других химических параметров. Например, при рассчете химических реакций и составления химических уравнений, числа позволяют определить пропорции веществ, участвующих в реакции.

Математика, как наука о числах, является основой для многих других научных дисциплин. Она используется в физике, химии, биологии, экономике и многих других областях для моделирования, прогнозирования и анализа данных. Например, в экономике числа используются для анализа финансовых показателей, прогнозирования рыночной ситуации и принятия решений на основе экономических моделей.

Биология также не обходится без чисел. Они используются для измерения биологических параметров, таких как рост, вес, количество клеток и т.д. Числа позволяют установить закономерности и связи между различными биологическими явлениями и сделать выводы о их функционировании.

Таким образом, числа играют важную роль во многих научных дисциплинах. Они позволяют измерять, описывать и анализировать различные явления и являются основой для построения математических моделей и прогнозирования результатов исследования.

Числа в экономике и финансах

Числа играют важную роль в экономике и финансах. Они используются для измерения и анализа различных экономических и финансовых показателей.

В экономике числа используются для оценки величины и изменений валового внутреннего продукта (ВВП), инфляции, безработицы и других макроэкономических показателей. Числа помогают экономистам анализировать и прогнозировать состояние и развитие экономики страны.

В финансах числа используются для оценки и анализа финансовых результатов и показателей компаний. Числа позволяют инвесторам и аналитикам принимать решения о вложениях и оценивать финансовое состояние компаний. Например, показатели, такие как выручка, прибыль, активы и долги, выражаются числами и используются для анализа финансовой устойчивости и эффективности компаний.

Также числа используются для расчета и представления денежных сумм и процентных ставок. В экономике и финансах часто встречаются такие понятия, как инфляция, процентная ставка, курс валюты, цена акций и другие, которые выражаются числами и помогают оценить экономическую ситуацию и принять решения.

ПоказательОписание

ВВП	Валовый внутренний продукт — сумма стоимости всех товаров и услуг, произведенных в стране за определенный период времени
Инфляция	Увеличение общего уровня цен на товары и услуги
Безработица	Количество людей, не имеющих работу и активно ищущих ее
Выручка	Сумма денег, полученных от продажи товаров или оказания услуг
Прибыль	Доход компании после вычета всех расходов и налогов

Таким образом, числа в экономике и финансах являются неотъемлемой частью анализа и оценки различных показателей и явлений. Они помогают принимать решения, планировать и прогнозировать экономическую и финансовую деятельность.

Числа в физике и инженерии

Числа играют важную роль в физике и инженерии, где они используются для описания и измерения физических величин.

В физике числа используются для выражения фундаментальных законов и принципов. Физические величины, такие как масса, скорость, сила, энергия и т. д., измеряются и выражаются числами. Например, закон всемирного тяготения Ньютона выражается числовым соотношением, где числа используются для определения силы притяжения между двумя телами.

В инженерии числа используются для проектирования и конструирования различных объектов и систем. Инженеры используют числа для определения размеров и параметров деталей, расчета нагрузок, прочности материалов и т. д. Например, при проектировании моста инженеры используют числа для определения необходимого размера и прочности конструкции, чтобы обеспечить безопасность и надежность моста.

Числа в физике и инженерии также используются для моделирования и решения математических задач. Физические и инженерные задачи могут быть представлены в виде математических моделей, где числа используются для описания и решения этих моделей. Например, числа используются для решения дифференциальных уравнений, описывающих физические процессы и явления.

Таким образом, числа являются неотъемлемой частью физики и инженерии, играя ключевую роль в описании и анализе физических явлений, проектировании и конструировании объектов и систем, а также в решении математических задач. Понимание и использование чисел является важным навыком для физиков и инженеров, позволяя им успешно работать в своих областях.

Числа и математические модели в компьютерных науках

В компьютерных науках числа и математические модели играют фундаментальную роль в решении различных задач. Числовые значения используются для представления данных, выполнения вычислений и моделирования реальных процессов.

Компьютерные науки занимаются разработкой алгоритмов и программ, которые могут обрабатывать и анализировать большие объемы данных. Числа являются основной единицей измерения этих данных и позволяют программам проводить различные операции, такие как сортировка, фильтрация, арифметические вычисления и т.д.

Математические модели используются для представления и анализа сложных систем. Они позволяют упростить реальность и описать ее с помощью формул и уравнений. Компьютерные науки применяют математические модели для решения задач в различных областях, таких как искусственный интеллект, компьютерная графика, криптография и многое другое.

Числа и математические модели в компьютерных науках позволяют строить точные и эффективные решения для сложных задач. Они предоставляют инструменты для анализа данных, создания алгоритмов и оптимизации процессов. Без использования чисел и математических моделей компьютерные науки не смогли бы достичь таких высоких результатов и применений в современном мире.

Развитие представления о числах в истории науки

Числа сопровождают человечество на протяжении всей его истории. С самых древних времен люди использовали числа для счета, измерения времени и пространства, а также для решения различных задач. В разных эпохах и культурах человеки разработали различные системы численности и способы представления чисел.

Одна из самых ранних систем численности была разработана древними Сумерами около 3000 года до нашей эры. Они использовали шестидесятиричную систему счисления, основанную на числе 60. Эта система все еще используется в некоторых областях, например, в измерении времени и углов.

В Древнем Египте разработали свою систему численности, основанную на числах 10 и 1. Они использовали специальные символы, называемые глифами, для представления чисел. Эта система стала основой для развития римской системы счисления.

В разные исторические периоды в разных частях света были разработаны различные системы численности, включая десятичную систему, которая является основной для современной науки. С развитием математики и научных открытий представление о числах становилось все более сложным и абстрактным.

Сегодня, благодаря научному прогрессу, мы имеем широкий спектр математических систем и символов для представления чисел, которые используются в науке и повседневной жизни. Понимание и использование чисел играют важную роль в науке, позволяя нам анализировать данные, строить графики, проводить эксперименты и делать выводы.

Вопрос-ответ:

Что такое число в математике?

Число в математике — это абстрактный объект, который используется для измерения и подсчета количества или для определения позиции в порядке.

Какое значение имеет число в математике?

Числа играют важную роль в математике. Они используются для решения уравнений, представления величин и измерений, а также для разработки математических моделей, которые помогают понять и описать различные явления в науке и реальном мире.

Какие типы чисел существуют в математике?

В математике существует несколько типов чисел, таких как натуральные числа, целые числа, рациональные числа и действительные числа. Также существуют комплексные числа, иррациональные числа, простые числа и другие.

Какова роль чисел в научных исследованиях?

Числа играют важную роль в научных исследованиях. Они позволяют ученым измерять и описывать явления, проводить статистический анализ данных, создавать математические модели, понимать законы природы и разрабатывать новые теории и гипотезы.

Какое значение имеет понятие числа в повседневной жизни?

В повседневной жизни числа используются для счета, измерения времени, расчета финансов, определения количества предметов и многих других целей. Они помогают нам понять и описать мир вокруг нас и сделать нашу жизнь более удобной и предсказуемой.

Что такое число в математике?

В математике число — это абстрактный объект, который используется для измерения и подсчета количества. Числа могут быть натуральными, целыми, рациональными, иррациональными, а также комплексными. Они обладают свойствами сложения, вычитания, умножения и деления, которые позволяют выполнять различные математические операции.

Какую роль числа играют в науке?

Числа играют ключевую роль в науке. Они используются для измерения и описания физических явлений, для формулирования законов и теорий, а также для представления данных и проведения вычислений. Например, в физике числа используются для измерения времени, расстояния, скорости и других физических величин. В химии числа используются для выражения массы, объема и концентрации веществ. В биологии числа используются для описания популяций, генетических кодов и других биологических процессов.

Видео по теме: