Что такое число математика

Число в математике — это абстрактное понятие, представляющее собой символ или комбинацию символов, используемых для измерения количества, порядка или размера. В математике числа разделяются на натуральные, целые, рациональные и иррациональные. Они являются основой для выполнения арифметических операций и решения уравнений. Число в математике является ключевым понятием и основой для понимания многих других математических концепций и теорий.

Число — это абстрактное понятие, используемое в математике для измерения количества, порядка или размера. Оно является одним из основных понятий математики, которое применяется во множестве различных областей и имеет множество свойств и характеристик.

Число может быть представлено как символ или последовательность символов, которые обозначают определенное количество или понятие. Оно может быть целым или десятичным, натуральным или отрицательным. В математике число может быть представлено в различных форматах, таких как десятичная, бинарная или римская системы счисления.

Существует множество свойств чисел, которые позволяют их сравнивать, складывать, вычитать, умножать и делить. К числам относятся также рациональные числа, которые могут быть представлены в виде дроби, и иррациональные числа, которые не могут быть представлены в виде дроби.

Числа играют важную роль во многих научных и инженерных областях, таких как физика, экономика, информатика и другие. Они используются для измерения, моделирования, решения задач и предсказания результатов экспериментов. Также числа являются неотъемлемой частью математических операций и формул, которые используются в науке, технике и других областях деятельности человека.

Число в математике: понятие и свойства

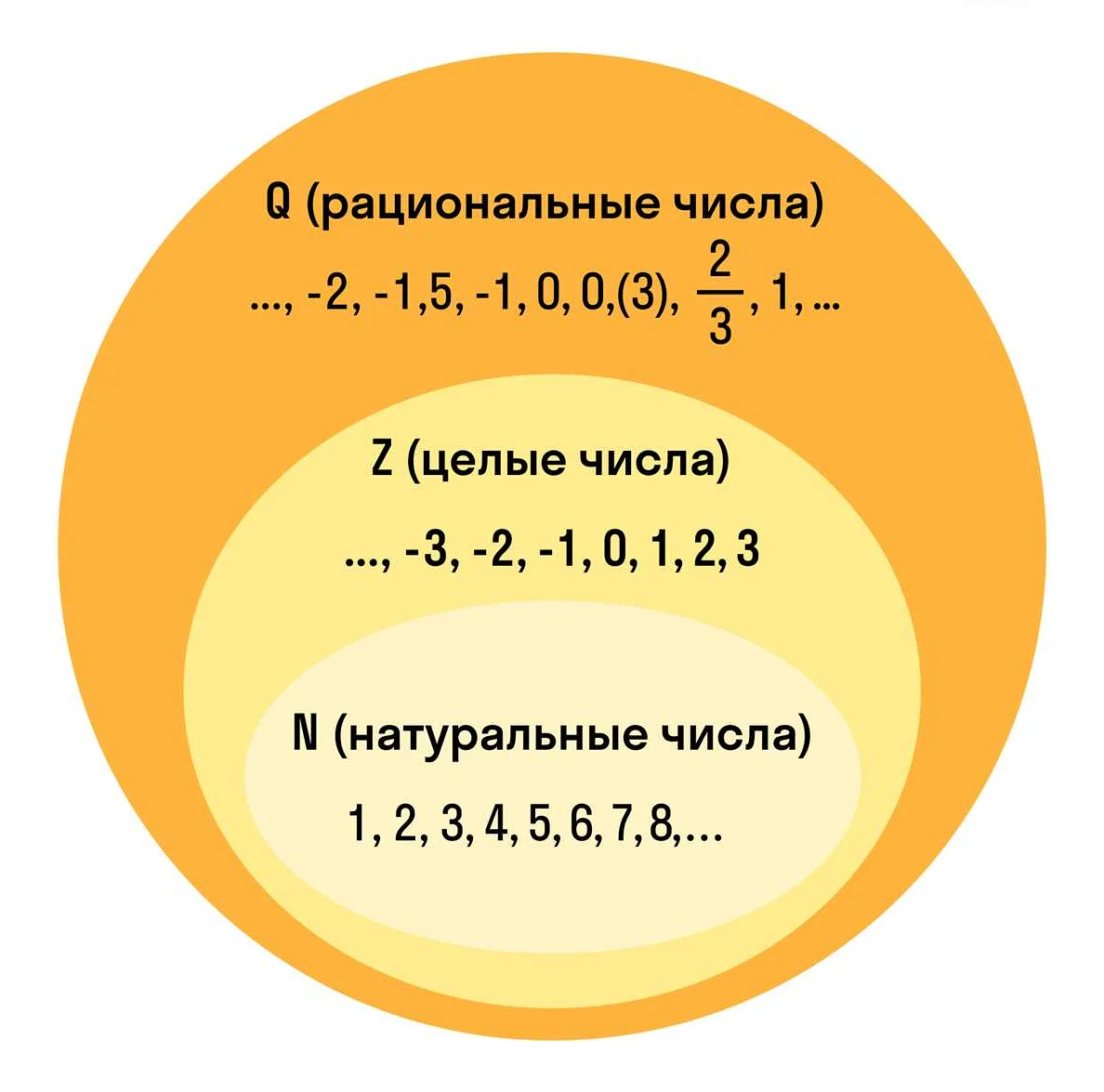
В математике существует множество различных типов чисел, таких как натуральные числа, целые числа, рациональные числа, иррациональные числа и дроби. Каждый тип чисел обладает своими уникальными свойствами и особенностями.

Свойства чисел позволяют совершать над ними различные операции, такие как сложение, вычитание, умножение и деление. Например, свойство коммутативности позволяет менять порядок слагаемых или множителей при сложении или умножении чисел без изменения результата.

Основные свойства чисел включают:

• Свойство ассоциативности — порядок выполнения операций не влияет на результат.
• Свойство дистрибутивности — операции сложения и умножения могут быть связаны друг с другом.
• Свойство идентичности — существует нейтральный элемент, который не изменяет значение числа при операции.
• Свойство обратности — для каждого числа существует обратное ему число, при сложении или умножении с которым получается нейтральный элемент.
• Свойство порядка — числа могут быть упорядочены по возрастанию или убыванию.

Знание и понимание понятия и свойств чисел является основой для решения различных математических задач и применения математики в реальной жизни. Математика и числа играют важную роль в различных науках, технике, физике, экономике и многих других областях.

Что такое число в математике

Числа в математике могут быть классифицированы по различным критериям, таким как рациональные числа, иррациональные числа, целые числа, натуральные числа и другие. Рациональные числа представляются в виде дробей, где числитель и знаменатель являются целыми числами. Иррациональные числа не могут быть представлены в виде дроби и имеют бесконечное количество десятичных знаков.

Числа в математике обладают рядом свойств, таких как ассоциативность, коммутативность и дистрибутивность. Ассоциативность означает, что результат операции не зависит от порядка группировки чисел. Коммутативность означает, что порядок чисел в операции не имеет значения. Дистрибутивность означает, что операции можно выполнять отдельно над каждым числом в выражении.

Числа в математике широко используются в различных областях, таких как физика, экономика, инженерия и т.д. Они позволяют точно измерять и описывать различные явления и процессы. Например, числа используются для решения уравнений, вычисления площадей и объемов, предсказания будущих тенденций и т.д.

Таким образом, число в математике играет важную роль и является неотъемлемой частью нашей жизни и познания мира.

Различные виды чисел

Математика изучает разные виды чисел, которые характеризуются своими особенностями и применением. В этом разделе мы рассмотрим некоторые из них.

Вид чиселОписаниеПримеры

Натуральные числа	Положительные целые числа, используемые для подсчета и упорядочивания объектов.	1, 2, 3, 4, 5, …
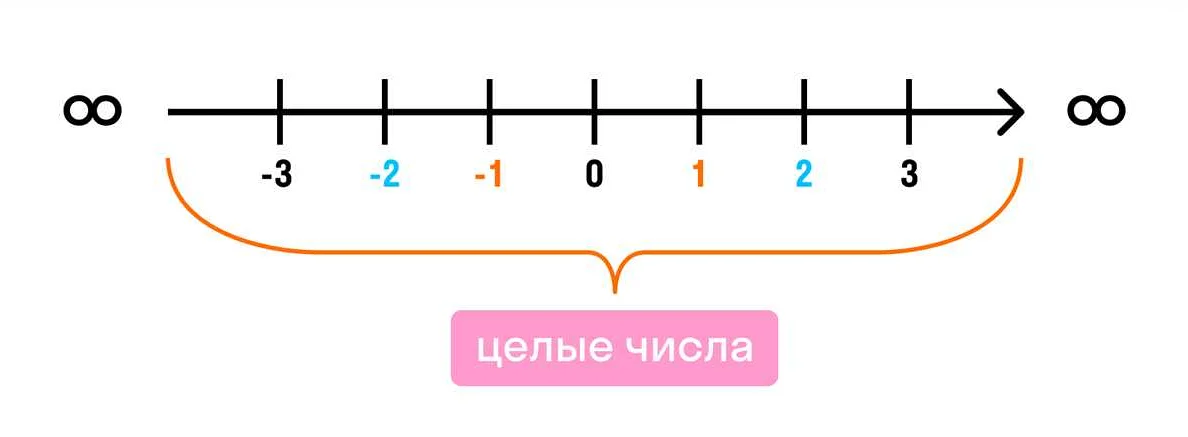
Целые числа	Набор натуральных чисел, включающий положительные, отрицательные и нуль.	…, -3, -2, -1, 0, 1, 2, 3, …
Рациональные числа	Числа, которые могут быть представлены в виде дроби, где числитель и знаменатель являются целыми числами.	1/2, -3/4, 5/8, 2, …
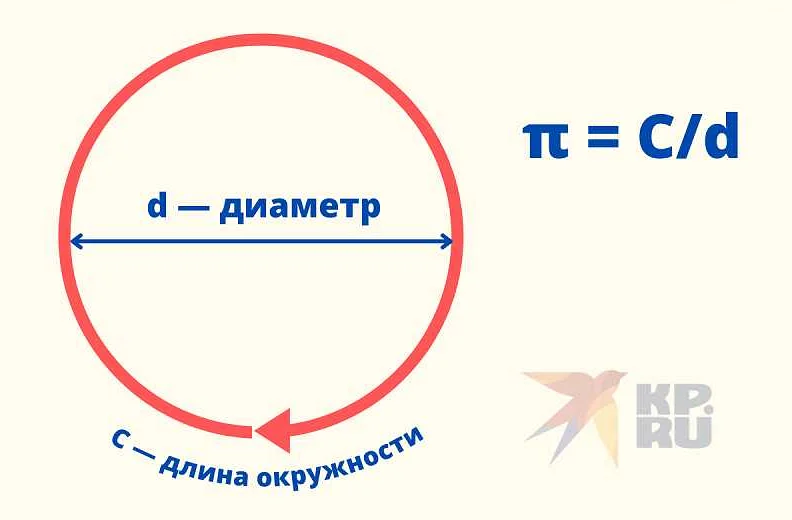
Иррациональные числа	Числа, которые не могут быть представлены в виде дроби и имеют бесконечное число десятичных знаков.	π (пи), √2 (квадратный корень из 2), …
Вещественные числа	Включают рациональные и иррациональные числа, представленные на числовой прямой.	-∞, …, -3, -2, -1, 0, 1, 2, 3, …, +∞

Это лишь несколько примеров видов чисел, которые используются в математике. Изучение их свойств и применение позволяют решать разнообразные задачи и проводить точные измерения в науке и технике.

Операции с числами

Среди основных операций с числами можно выделить:

1. Сложение — операция, которая позволяет складывать два или более числа и получать их сумму. Например, 2 + 3 = 5.
2. Вычитание — операция, которая позволяет вычитать одно число из другого и получать их разность. Например, 5 — 3 = 2.
3. Умножение — операция, которая позволяет умножать одно число на другое и получать их произведение. Например, 2 * 3 = 6.
4. Деление — операция, которая позволяет делить одно число на другое и получать их частное. Например, 6 / 3 = 2.

Кроме основных операций, существуют также другие операции с числами, такие как возведение в степень, извлечение корня, нахождение остатка от деления и др. Они позволяют производить более сложные математические операции и решать более сложные задачи.

Операции с числами имеют ряд свойств, которые помогают совершать вычисления и проводить различные преобразования. Например, свойства операций сложения и умножения (ассоциативность, коммутативность, дистрибутивность) позволяют менять порядок и группировку чисел при вычислениях, не изменяя результата операции.

Операции с числами имеют широкое применение в различных областях. Например, в финансовой математике они используются для расчета процентов, сумм кредитов и других финансовых показателей. В физике операции с числами позволяют решать задачи о движении тела, силе, энергии и других физических явлениях. В программировании операции с числами используются для решения различных задач и алгоритмов.

Свойства чисел

• Коммутативность: Сложение и умножение чисел коммутативны, то есть порядок, в котором числа складываются или умножаются, не влияет на результат. Например, a + b = b + a и a * b = b * a.
• Ассоциативность: Сложение и умножение чисел ассоциативны, то есть можно менять расстановку скобок при выполнении операций без изменения результата. Например, (a + b) + c = a + (b + c) и (a * b) * c = a * (b * c).
• Дистрибутивность: Умножение числа на сумму двух чисел равно сумме произведений этого числа на каждое из этих чисел. Например, a * (b + c) = (a * b) + (a * c).
• Идентичность: Существуют нейтральные элементы для сложения и умножения, которые не изменяют другие числа. Например, a + 0 = a и a * 1 = a.
• Обратимость: Каждое число имеет обратное число, при сложении с которым получается нейтральный элемент. Например, a + (-a) = 0 и a * (1/a) = 1 (для a ≠ 0).
• Порядок: На числах можно определить отношение порядка, которое позволяет сравнивать и упорядочивать числа. Существуют такие отношения, как «меньше», «больше», «меньше или равно» и «больше или равно».

Это лишь некоторые из основных свойств чисел, которые играют важную роль в математике и имеют широкое применение в различных областях науки и повседневной жизни.

Числа в математических системах

Числа играют важную роль в математике и используются для измерения, счета, описания и анализа количественных характеристик. В математике существуют различные системы чисел, каждая из которых имеет свои особенности и применения.

Одна из наиболее распространенных систем чисел — это десятичная система. В десятичной системе числа представляются с помощью десяти символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. В этой системе каждая позиция числа имеет свой вес, который определяется степенью десяти. Например, число 1234 в десятичной системе значит 1*10^3 + 2*10^2 + 3*10^1 + 4*10^0.

Однако, помимо десятичной системы, существуют и другие системы чисел. Например, бинарная система использует только два символа — 0 и 1, и каждая позиция числа имеет вес, который определяется степенью двойки. Также существуют восьмеричная и шестнадцатеричная системы, которые используют восьмеричную и шестнадцатеричную системы счисления соответственно.

Кроме того, в математике существуют комплексные числа, которые представляют собой комбинацию вещественной и мнимой частей. Комплексные числа записываются в виде a + bi, где a и b — вещественные числа, а i — мнимая единица, удовлетворяющая условию i^2 = -1.

Разные системы чисел имеют свои применения в различных областях математики и естественных науках. Например, бинарная система широко используется в электронике и компьютерной науке, а комплексные числа являются основой для решения многих математических задач и применяются в физике и инженерии.

Понимание различных систем чисел позволяет математикам и ученым эффективно работать с числами и решать разнообразные задачи, от простых арифметических операций до сложных математических моделей и уравнений.

Числа в науках и технологиях

В физике, химии и других естественных науках числа используются для описания физических величин и проведения математических расчетов. Например, в физике используются числа для измерения массы, длины, времени и других физических характеристик. Эти числа позволяют ученым проводить эксперименты, строить модели и прогнозировать результаты исследований.

В технологиях числа также играют важную роль. Компьютеры, смартфоны, автомобили и другие технические устройства основаны на использовании чисел и математических алгоритмов. Числа используются для хранения и обработки данных, решения различных задач и создания новых технических решений. Например, в программировании числа используются для описания переменных, выполнения математических операций и создания сложных программных алгоритмов.

Кроме того, числа широко применяются в статистике и экономике. В статистике числа используются для анализа данных, проведения опросов и создания статистических моделей. В экономике числа используются для расчета стоимости товаров и услуг, прогнозирования спроса и предложения, анализа финансовых показателей и многих других задач.

Таким образом, числа играют важную роль в науках и технологиях, помогая ученым и инженерам понимать и описывать мир вокруг нас, а также создавать новые технические решения и улучшать существующие технологии.

Роль чисел в жизни человека

В обычной повседневной жизни мы постоянно сталкиваемся с числами. Мы считаем деньги, измеряем время, оцениваем расстояния. Числа позволяют нам точно описывать количество и размеры предметов, событий и процессов.

Числа необходимы также в науке. Они помогают ученым измерять и описывать физические явления, математику, химию, физику и другие естественные и точные науки. Без чисел невозможно проводить точные эксперименты и делать точные измерения.

Числа играют важную роль в экономике и финансах. Они позволяют нам управлять деньгами, рассчитывать доходы и расходы, анализировать статистику и прогнозировать будущие результаты.

Кроме того, числа являются основой для математических вычислений и операций. Они позволяют нам складывать, вычитать, умножать и делить, решать уравнения и задачи, анализировать данные и находить закономерности.

В целом, числа являются неотъемлемой частью нашей жизни. Они помогают нам понять и взаимодействовать с миром, а также решать разнообразные задачи и проблемы. Без чисел было бы очень сложно представить себе современный мир и все его достижения.

Вопрос-ответ:

Как определить понятие числа в математике?

Число в математике — это абстрактный объект, который используется для измерения количества или размера. Оно является основой для выполнения математических операций и решения различных задач.

Какие свойства имеют числа в математике?

Числа в математике обладают рядом свойств, таких как коммутативность (меняя порядок слагаемых или множителей, результат не меняется), ассоциативность (порядок выполнения операций не влияет на результат), дистрибутивность (умножение числа на сумму равно сумме произведений), и многое другое.

Какие применения имеет число в математике?

Числа в математике имеют широкое применение в различных областях. Они используются для измерения, моделирования, решения уравнений, описания законов природы, анализа данных и многого другого. Они являются неотъемлемой частью науки и технологий.

Какие виды чисел существуют в математике?

В математике существует множество различных видов чисел. К ним относятся натуральные числа (1, 2, 3 и так далее), целые числа (натуральные числа вместе с их отрицаниями и нулем), рациональные числа (числа, представимые дробью), иррациональные числа (непредставимые дробью числа, такие как корень из двух) и действительные числа (объединение рациональных и иррациональных чисел).

Какие операции можно выполнять с числами в математике?

С числами в математике можно выполнять различные операции, такие как сложение, вычитание, умножение, деление, возведение в степень, извлечение корня и другие. Эти операции позволяют решать задачи, проводить исследования и делать выводы в различных областях знаний.

Что такое число в математике?

Число в математике — это абстрактный объект, который используется для измерения, счета, манипуляций и решения математических задач. Оно представляет собой абстрактную идею о количестве или порядке чего-либо. Числа могут быть натуральными, целыми, рациональными или иррациональными в зависимости от своих свойств и признаков.

Какие свойства имеют числа в математике?

Числа в математике обладают рядом свойств и характеристик. Они могут быть положительными или отрицательными, четными или нечетными, простыми или составными. Кроме того, числа могут быть взаимно простыми, рациональными или иррациональными. Они могут быть представлены в различных форматах, таких как десятичная, дробная или научная запись. К числам также применяются математические операции, такие как сложение, вычитание, умножение и деление.

Применение чисел в разных областях

Одной из основных областей, где применяются числа, является физика. Числа используются для описания физических явлений, проведения экспериментов и решения уравнений. Например, в механике числа используются для расчета траекторий движения тел и сил, действующих на них.

В химии числа используются для определения массы вещества, концентрации растворов и проведения химических расчетов. Они помогают установить соотношение между реагентами и продуктами химической реакции.

В экономике и финансах числа используются для анализа финансовых данных, прогнозирования тенденций рынка, расчета индексов и показателей эффективности. Они позволяют принимать обоснованные решения в области инвестиций и управления бизнесом.

В информатике числа используются для представления и обработки данных, алгоритмов и программирования. Они используются для хранения и передачи информации, вычислений и разработки компьютерных моделей.

В математике числа являются основным объектом изучения. Они используются для формулирования и доказательства теорем, решения уравнений и разработки математических моделей. Они играют ключевую роль во всех областях математики, таких как алгебра, геометрия, анализ и теория вероятностей.

Область примененияПримеры

Физика	Расчет скорости, ускорения и силы
Химия	Определение массы вещества, концентрации растворов
Экономика и финансы	Анализ финансовых данных, прогнозирование рынка
Информатика	Хранение и передача данных, программирование
Математика	Формулирование и доказательство теорем, решение уравнений

Видео по теме: