Что обозначает кратно в математике

Кратное число в математике — это число, которое делится на другое число без остатка. Узнайте, как определить, что число кратное, и как использовать это понятие в различных математических операциях.

В математике понятие «кратное» является одним из основных и используется в различных областях этой науки. Кратное — это число, которое делится на другое число без остатка. Другими словами, если одно число является кратным другого, то оно делится на это число без остатка, а результат деления — целое число.

Например, пусть у нас есть число 12. Если мы разделим это число на 3, то получим 4. Таким образом, число 12 является кратным числа 3.

Кратность может быть выражена с помощью знака деления нацело (деление без остатка) или с помощью математической записи, в которой целое число, делящееся на другое число, помещается над знаком деления.

Пример: 12 : 3 = 4

Кратность также может быть использована для описания отношения одного числа к другому. Например, если число A является кратным числа B, то можно сказать, что A кратно B или B кратит A.

Знание понятия кратности является важным в математике, так как оно используется во многих областях, включая арифметику, алгебру, геометрию и теорию чисел. Понимание кратности позволяет решать различные задачи и проводить различные операции с числами.

Кратное в математике: определение и примеры

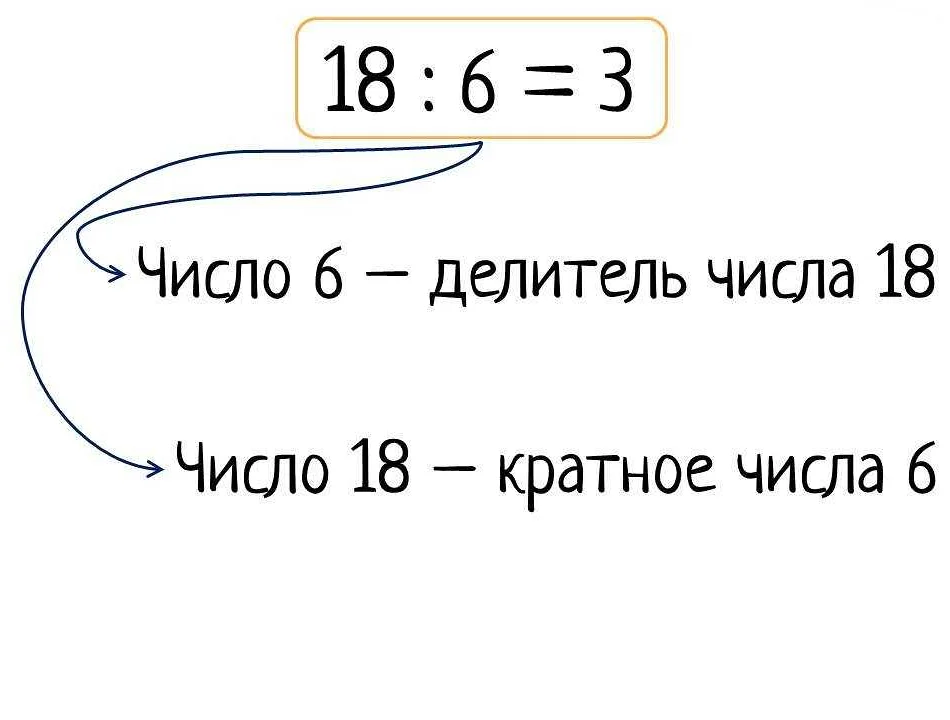
В математике термин «кратное» используется для описания отношения между двумя числами.

Число А называется кратным числа В, если оно делится на число В без остатка. Иными словами, если при делении числа А на число В результат равен целому числу, то А является кратным числа В.

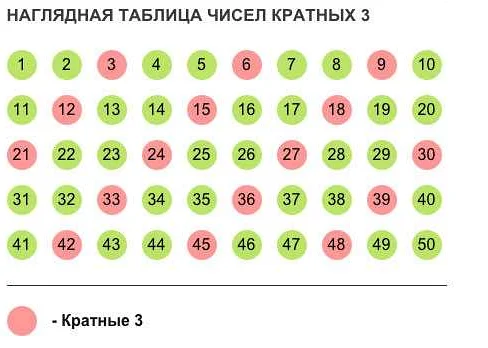
Для более наглядного примера можно рассмотреть таблицу кратных чисел:

ЧислоКратное числу 2Кратное числу 3Кратное числу 5

2	Да	Нет	Нет
3	Нет	Да	Нет
4	Да	Нет	Нет
5	Нет	Нет	Да
6	Да	Да	Нет

Из таблицы видно, что число 2 кратно числу 2 (потому что 2 делится на 2 без остатка), но не кратно числу 3 и 5. Число 3 кратно числу 3, но не кратно числу 2 и 5. Число 6 кратно и числу 2, и числу 3, но не кратно числу 5.

Таким образом, понимание понятия кратного числа в математике важно для решения различных задач и задачек, а также для более глубокого понимания сущности чисел и их взаимосвязей.

Что такое кратное в математике?

Например, число 10 является кратным числу 5, потому что оно делится на 5 без остатка. Также число 12 кратно числу 3, так как 12 делится на 3 без остатка.

Для определения, является ли число кратным другому числу, можно использовать деление с остатком. Если при делении одного числа на другое получается остаток равный нулю, то первое число является кратным второму числу.

Существуют различные способы определения кратности чисел. Например, для определения кратности числу 4 можно использовать факт, что кратные числа 4 имеют последние две цифры, образующие число кратное 4. Таким образом, числа 12, 16, 20 и т.д. являются кратными числу 4, потому что их последние две цифры образуют число кратное 4.

Кратные числа играют важную роль в математике, особенно в арифметике и алгебре. Они используются для решения различных задач, таких как нахождение общего кратного двух чисел или нахождение наименьшего общего кратного.

Как определить кратное числа?

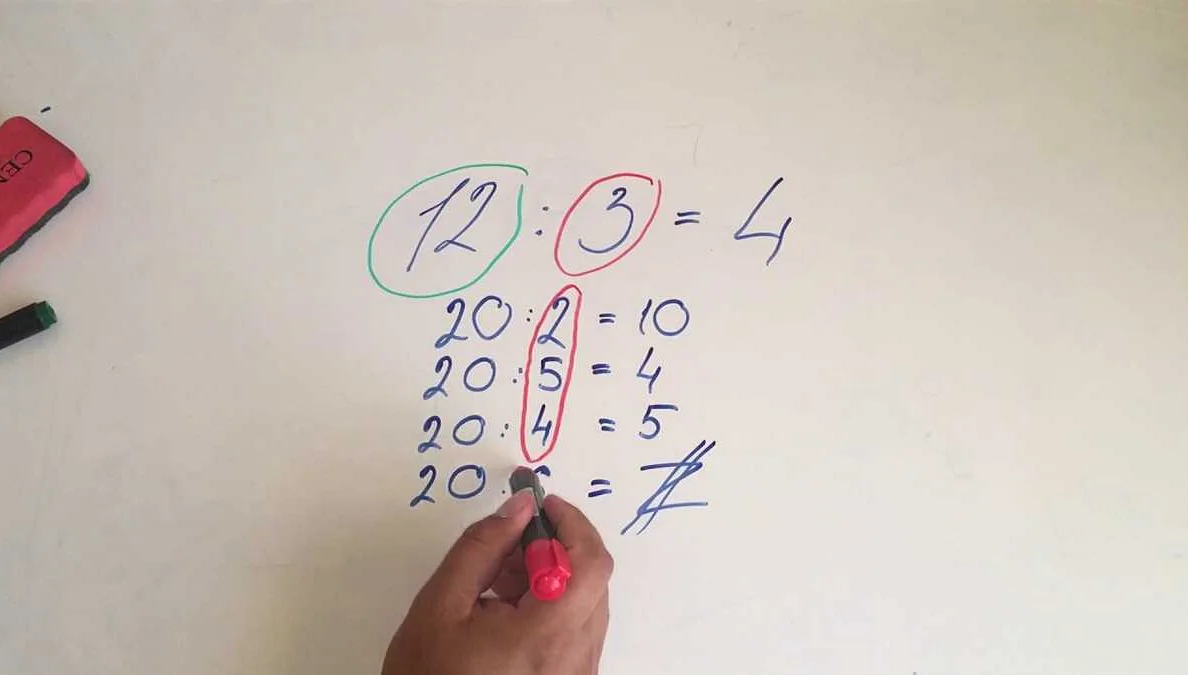
Для определения кратности числа можно использовать математическую операцию деления с остатком. Если при делении числа на другое число остаток равен нулю, то первое число является кратным второму.

Например, число 10 является кратным числу 5, так как при делении 10 на 5 получается остаток равный нулю. А число 15 не является кратным числу 7, так как при делении 15 на 7 остаток не равен нулю.

Кратность числа может быть положительной или отрицательной. Если число делится на другое число без остатка, то оно является положительно кратным. Если же число делится на другое число без остатка, но полученный результат умножен на -1, то оно является отрицательно кратным.

Примеры кратных чисел

Кратным числом называется число, которое делится на другое число без остатка. Вот несколько примеров:

• Число 10 кратно числу 5, потому что 10 делится на 5 без остатка.
• Число 15 кратно числу 3, потому что 15 делится на 3 без остатка.
• Число 24 кратно числу 6, потому что 24 делится на 6 без остатка.

Кратные числа могут быть отрицательными. Например, -12 кратно числу 4, потому что -12 делится на 4 без остатка.

Кратное числа и деление без остатка

Деление без остатка можно представить с помощью символа % — остаток от деления. Если при делении числа a на число b остаток равен нулю (% a b = 0), то число a является кратным числа b.

Кратность числа может быть использована для различных задач. Например, при работе с временем, если нужно найти кратное число часов или минут, можно использовать понятие кратности. Также кратность может быть полезной при работе с массивами или циклами, где нужно проверить, является ли число кратным или нет.

Определение кратности числа помогает нам лучше понять и использовать математические операции для решения задач различной сложности.

Кратное и некратное число: в чем разница?

Когда речь заходит о числах, в математике выделяют два основных понятия: кратное и некратное число. Эти термины относятся к делению одного числа на другое и указывают на результат этого деления.

Кратное число — это число, которое делится на другое число без остатка. Другими словами, если одно число делится на другое и результатом этого деления является целое число, то первое число называется кратным второму числу. Например, число 10 кратно числу 5, так как 10 делится на 5 без остатка.

Некратное число — это число, которое не делится на другое число без остатка. Если при делении одного числа на другое получается остаток, то первое число называется некратным второму числу. Например, число 7 не является кратным числу 3, так как при делении 7 на 3 получается остаток 1.

Использование понятий кратного и некратного числа в математике позволяет более точно описывать и анализировать взаимосвязи между числами. Они являются основой для решения различных задач, основанных на арифметических операциях деления и умножения.

ПримерКратное числоНекратное число

Число 15	Кратно числу 3	Некратно числу 4
Число 10	Кратно числу 5	Некратно числу 7
Число 24	Кратно числу 6	Некратно числу 9

Видео по теме:

Вопрос-ответ:

Что значит кратно в математике?

В математике, говоря о числах, одно число является кратным другого, если оно делится на него без остатка.

Как определить, что одно число кратно другому?

Чтобы определить, что одно число кратно другому, нужно убедиться, что при делении первого числа на второе получается ноль в остатке.

Какие примеры можно привести для кратных чисел?

Например, число 9 кратно числу 3, так как оно делится на 3 без остатка. Также число 16 кратно числу 4, так как оно делится на 4 без остатка.

Можно ли сказать, что число кратно самому себе?

Да, любое число кратно самому себе. Например, число 5 кратно числу 5, так как оно делится на 5 без остатка.

В чем отличие кратных чисел от делителей?

Кратные числа — это числа, на которые можно делить другое число без остатка. Делители — это числа, на которые можно делить другое число с остатком.

Как определить, что одно число кратно другому?

Одно число считается кратным другому, если оно делится на него без остатка. Например, число 15 кратно числу 3, так как 15 делится на 3 без остатка.

Может ли число быть кратным самому себе?

Да, число может быть кратным самому себе. Например, число 8 является кратным 8, так как 8 делится на 8 без остатка.

Кратное число и его свойства

Основные свойства кратных чисел:

1. Деление без остатка: Кратное число делится на другое число без остатка. Если a является кратным числом для b, то a делится на b без остатка.

2. Умножение: Если a и b — кратные числа для c, то их произведение a * b также будет кратным числом для c.

3. Сложение: Если a и b — кратные числа для c, то их сумма a + b также будет кратным числом для c.

Кратные числа широко применяются в различных областях математики и науки. Например, в алгебре кратные числа используются для решения уравнений и систем уравнений. В геометрии они помогают определить геометрические фигуры и их свойства. В физике кратные числа используются для измерения физических величин и установления закономерностей в природе.

Понимание кратных чисел и их свойств является важной основой для понимания более сложных математических концепций и применения их на практике.

Применение кратных чисел в практике

Кратные числа позволяют с легкостью выполнять деление и умножение. Например, если мы знаем, что число A кратно числу B, то мы можем с легкостью найти результат деления A на B. Также, зная кратное число, мы можем легко найти результат умножения числа на это кратное. Например, если число A кратно B, то мы можем найти результат умножения A на B, просто умножая число A на коэффициент, равный B.

Кратные числа также широко применяются в области геометрии. Например, если мы имеем отрезок, длина которого является кратной числа, то мы можем разделить этот отрезок на равные части. Также, кратные числа могут быть использованы для построения прямых линий, окружностей и других геометрических фигур.

Кратные числа также находят применение в физике. Например, если мы имеем закономерность, что волны с определенной частотой повторяются через равные промежутки времени, то можно сказать, что частота волн кратна периоду. Также, кратные числа могут быть использованы для расчетов времени, скорости и других физических величин.

В заключение, кратные числа имеют широкое применение в различных областях практики. Они позволяют упростить расчеты, деление и умножение, а также использоваться в геометрии и физике. Поэтому знание кратных чисел является важным для решения практических задач.