Что означает слово кратное в математике определение

Кратное число в математике обозначает число, которое делится на другое число без остатка. Узнайте, как определить кратность числа и как она используется в различных математических задачах.

В математике понятие «кратное» является одним из основных и используется для указания отношения между двумя числами. Кратное число является результатом умножения одного числа на другое, при этом второе число является множителем.

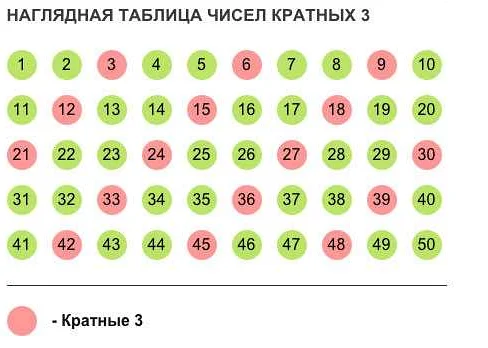
Когда говорят, что одно число является кратным другого, это означает, что первое число делится на второе без остатка. Например, число 12 является кратным числу 3, потому что его можно поделить на 3 три раза без остатка.

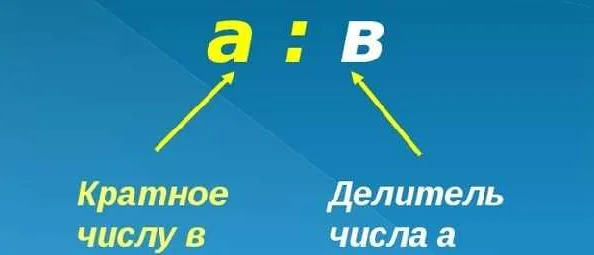
Математически это можно записать следующим образом: если число a делится на число b без остатка, то говорят, что a кратно b. В этом случае число b называется множителем, а число a — кратным.

Например, число 15 является кратным чисел 3 и 5, потому что оно делится на оба этих числа без остатка. Также число 30 является кратным чисел 2, 3, 5 и 10.

Понимание понятия «кратное» имеет важное значение в различных областях математики, включая арифметику, алгебру и численные методы. Оно используется для решения различных задач, в том числе для нахождения наибольшего общего делителя двух чисел, разложения чисел на простые множители и других математических операций.

Кратное число в математике: определение и значение

Например, число 10 является кратным числу 5, так как оно делится на 5 без остатка. А число 15 является кратным числу 3, так как оно делится на 3 без остатка.

Кратные числа широко используются в различных областях математики. Например, в арифметике кратные числа используются при решении задач на сумму и произведение чисел. В теории чисел кратные числа являются важными элементами для изучения свойств числовых последовательностей.

Также, кратные числа находят применение в реальных задачах. Например, при планировании расписания, когда нужно определить, через какое количество времени наступит определенное событие, или при расчете количества материала, необходимого для производства определенного количества изделий.

Итак, кратное число в математике — это число, которое делится на другое число без остатка. Знание о кратных числах помогает в решении различных задач и является важным элементом в изучении свойств чисел и числовых последовательностей.

Что такое кратное число?

Для определения кратности числа, необходимо сравнить его с другим числом и увидеть, делится ли одно на другое без остатка. Если деление происходит без остатка, то первое число является кратным второму.

Например, число 12 является кратным числа 3, так как 12 делится на 3 без остатка (12 ÷ 3 = 4). Также число 15 является кратным числа 5, так как 15 делится на 5 без остатка (15 ÷ 5 = 3).

Часто вместо термина «кратное число» используется также термин «делитель», который описывает число, на которое выполняется деление без остатка.

Кратные числа имеют множество применений в математике, а также в реальной жизни. Например, они используются для определения периодичности и повторяемости процессов, для нахождения общего кратного двух или более чисел, а также для решения задач, связанных с распределением и делением объектов.

Определение кратного числа

В математике, кратным числом называется число, которое делится на другое число без остатка. Другими словами, если при делении одного числа на другое остаток равен нулю, то первое число называется кратным второго числа.

Формально, число a называется кратным числа b, если существует целое число k такое, что a = b * k. Здесь a — кратное число, b — основное число, k — целое число, на которое a делится без остатка.

Например, число 10 является кратным числа 5, так как 10 = 5 * 2. Также, число 15 кратно числу 3, так как 15 = 3 * 5.

Кратные числа широко используются в алгебре и арифметике для решения различных задач и упрощения вычислений. Они играют важную роль в различных областях математики и науки.

Основное число (b)Кратные числа (a)

2	4, 6, 8, 10, …
3	6, 9, 12, 15, …
5	10, 15, 20, 25, …

Как определить кратность числа?

Для определения кратности числа необходимо выполнить следующие шаги:

1. Выберите число, которое вы хотите проверить на кратность.
2. Выберите число, на которое вы хотите разделить первое число.
3. Выполните деление первого числа на второе.
4. Если результат деления является целым числом без остатка, то первое число кратно второму числу.
5. Если результат деления имеет остаток, то первое число не кратно второму числу.

Например, чтобы определить, кратно ли число 12 числу 4, мы делим 12 на 4. Результат деления равен 3, что является целым числом без остатка. Следовательно, число 12 кратно числу 4.

Таким образом, определение кратности числа основано на выполнении деления и проверке наличия остатка. Если остаток от деления равен нулю, то число является кратным, в противном случае — не кратным.

Значение кратного числа в математике

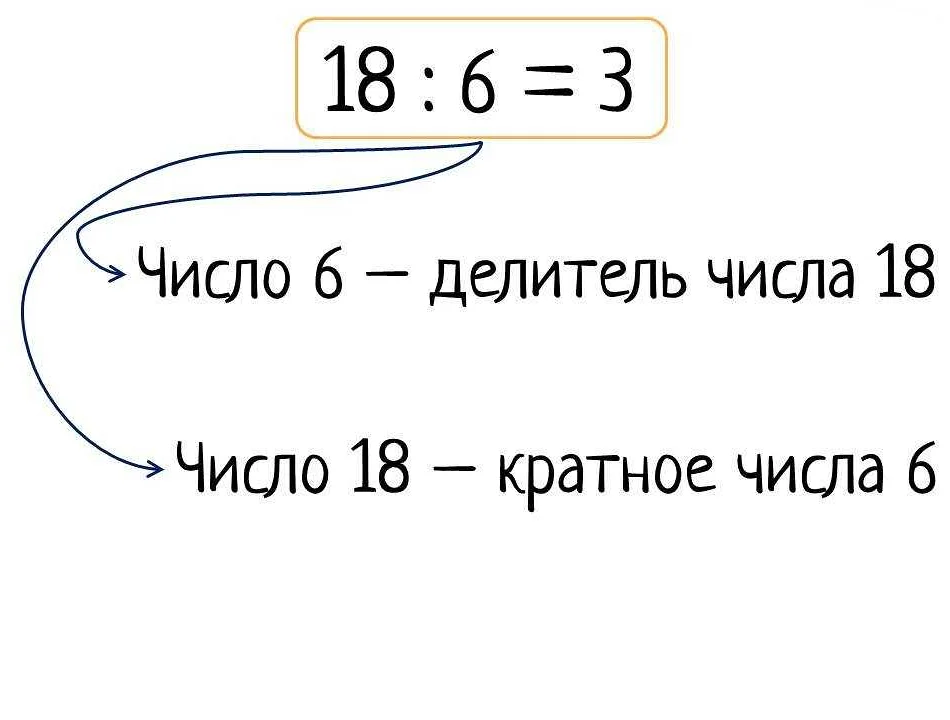
Например, если число 6 делится на число 2 без остатка, то число 6 является кратным числом числа 2.

Кратность числа может быть определена с помощью операции деления. Если результат деления двух чисел является целым числом, то первое число является кратным второго числа.

Кратные числа широко используются в математике, особенно в арифметике и алгебре. Они играют важную роль в решении уравнений, нахождении общего делителя, построении графиков и многих других математических операциях.

Важно отметить, что нуль (0) является кратным любого числа, так как при умножении на ноль результат всегда будет нулем.

Кратные числа и их свойства

Основные свойства кратных чисел:

1. Если число a является кратным числа b, то число b является делителем числа a.
2. Если число a кратно числу b, а число b кратно числу c, то число a кратно числу c.
3. Кратное числа имеют одинаковые остатки при делении на одно и то же число.
4. Кратное числа можно складывать и вычитать друг из друга, результат будет кратным этим числам.

Например, число 10 кратно числу 5, так как 10 можно представить как 5 умноженное на 2. Также число 15 кратно числу 5, так как 15 можно представить как 5 умноженное на 3.

Кратные числа имеют важное значение в математике, особенно при решении задач на делимость, нахождение общих кратных и других задачах.

Видео по теме:

Вопрос-ответ:

Как определить слово «кратное» в математике?

В математике слово «кратное» используется для описания отношения между двумя числами. Одно число называется кратным другому, если оно делится на него без остатка. Например, число 8 является кратным числа 4, так как 8 делится на 4 без остатка.

Какое значение имеет слово «кратное» в математике?

В математике слово «кратное» обозначает отношение между двумя числами, где одно число делится на другое без остатка. Таким образом, если число a кратно числу b, то число a можно представить в виде b * n, где n — целое число. Например, число 12 кратно числу 3, так как 12 = 3 * 4.

Как можно определить, что одно число кратно другому?

Чтобы определить, что одно число кратно другому, нужно проверить, делится ли первое число на второе без остатка. Если делится, то первое число кратно второму. Например, чтобы определить, что число 15 кратно числу 5, нужно разделить 15 на 5. Если результат деления равен целому числу, то число 15 кратно 5.

В каких случаях число не является кратным другому числу?

Число не является кратным другому числу, если оно не делится на него без остатка. Например, число 7 не является кратным числу 3, так как при делении 7 на 3 получается остаток. В этом случае говорят, что числа не имеют отношения «кратности».

Примеры кратных чисел

Кратность числа относительно другого числа означает, что первое число можно разделить на второе без остатка. В математике это отношение обозначается как «a кратно b» или «a делится на b». Вот несколько примеров кратных чисел:

Пример 1: Число 12 кратно числу 3, так как 12 делится на 3 без остатка (12 ÷ 3 = 4).

Пример 2: Число 20 кратно числу 5, так как 20 делится на 5 без остатка (20 ÷ 5 = 4).

Пример 3: Число 36 кратно числу 6, так как 36 делится на 6 без остатка (36 ÷ 6 = 6).

Пример 4: Число 100 кратно числу 10, так как 100 делится на 10 без остатка (100 ÷ 10 = 10).

Таким образом, кратные числа являются результатом деления одного числа на другое без остатка.

Кратность чисел в арифметических операциях

Кратность чисел играет важную роль в арифметических операциях, таких как сложение, вычитание, умножение и деление.

При сложении чисел, кратность определяет, насколько раз нужно прибавить одно число к другому. Например, если число 4 кратно числу 2, то мы можем сложить их и получить результат 6.

При вычитании чисел, кратность определяет, сколько раз можно вычесть одно число из другого. Например, если число 6 кратно числу 3, то мы можем вычесть 3 из 6 и получить результат 3.

При умножении чисел, кратность определяет, сколько раз нужно умножить одно число на другое. Например, если число 5 кратно числу 2, то мы можем умножить их и получить результат 10.

При делении чисел, кратность определяет, сколько раз одно число содержится в другом. Например, если число 8 кратно числу 4, то мы можем разделить 8 на 4 и получить результат 2.

Таким образом, кратность чисел играет важную роль в арифметических операциях, помогая определить результаты этих операций.

Арифметическая операцияПримерКратность

Сложение	2 + 4	4 кратно 2
Вычитание	6 — 3	6 кратно 3
Умножение	5 * 2	5 кратно 2
Деление	8 / 4	8 кратно 4