Что такое кратное 5 класс математика

В математике кратным числом называется число, которое делится на данное число без остатка. В 5 классе математики дети изучают понятие кратности, а также учатся находить кратные числа, используя различные методы и свойства деления. Ознакомьтесь с основными принципами и правилами кратности в пятом классе математики.

Кратное в математике — это число, которое делится на другое число без остатка. В классе математики, кратные числа являются одной из основных тем, которые изучают учащиеся. Понимание понятия кратного и умение определять кратность чисел является важным навыком, который поможет решать различные задачи и упрощать вычисления.

Для определения, является ли число кратным другому числу, необходимо проверить делится ли первое число на второе без остатка. Если деление выполняется без остатка, то число является кратным. Например, число 15 является кратным числу 5, так как 15 делится на 5 без остатка.

Пример:

Определите, является ли число 25 кратным числу 5.

Решение: Для того чтобы определить, является ли число 25 кратным 5, необходимо проверить, делится ли 25 на 5 без остатка. Если деление выполняется без остатка, то число 25 является кратным 5. В данном случае, 25 делится на 5 без остатка, следовательно, число 25 кратно числу 5.

Понимание кратности чисел помогает в решении различных задач. Например, если нужно определить, сколько чисел в диапазоне от 1 до 100 являются кратными числу 5, можно просто поделить 100 на 5 и получить ответ 20. Таким образом, в данном диапазоне 20 чисел являются кратными числу 5.

Изучение кратности чисел поможет развить навыки логического мышления и абстрактного мышления, а также применять математические знания в повседневной жизни.

Определение понятия «кратное» в математике

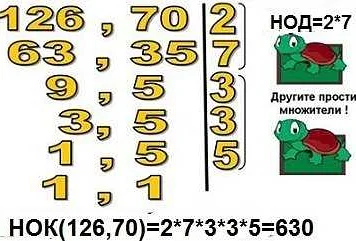
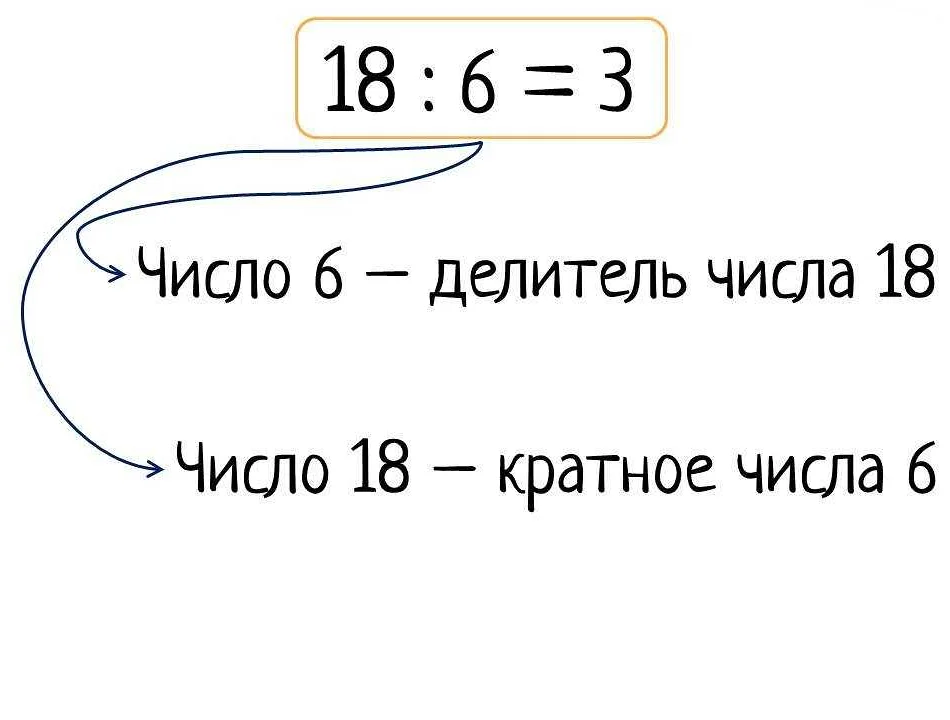
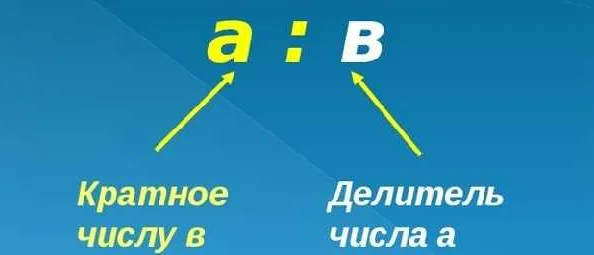
Например, если число 15 делится без остатка на число 5, то говорят, что 15 — кратное 5. Это можно записать так: 15 делится нацело на 5.

Также можно сказать, что 5 является делителем числа 15, а 15 — кратным числом 5.

Кратные числа можно определить с помощью деления: если результат деления двух чисел является целым числом, то первое число кратно второму.

Например: если 30 делится нацело на 6, то говорят, что 30 — кратное 6.

Знание понятия «кратное» позволяет решать множество задач и применять его в различных областях математики и реальной жизни.

Как определить, является ли число кратным 5

Если число делится на 5 без остатка, то оно является кратным 5. Например, число 10 является кратным 5, так как 10 ÷ 5 = 2, остаток от деления равен 0.

Если число не делится на 5 без остатка, то оно не является кратным 5. Например, число 7 не является кратным 5, так как 7 ÷ 5 = 1, остаток от деления равен 2.

Другим способом определить, является ли число кратным 5, является проверка последней цифры числа. Если последняя цифра числа равна 0 или 5, то число является кратным 5. Например, числа 20, 35 и 50 являются кратными 5, так как их последние цифры равны 0 или 5.

Правила делимости для чисел на 5

Если число оканчивается на 0 или 5, то оно обязано делиться на 5 без остатка. Например, число 35 не делится на 5, так как его последняя цифра равна 5, но число 40 делится на 5, так как его последняя цифра равна 0.

Кроме того, если число делится на 5, то оно также делится на 10, так как 10 является кратным числом 5. Например, число 20 делится на 5 и на 10.

Делимость числа на 5 можно использовать для определения кратности. Например, чтобы определить, является ли число кратным 5, достаточно проверить его последнюю цифру. Если она равна 0 или 5, то число кратно 5.

Как найти все кратные числа в заданном диапазоне

Для примера, рассмотрим задачу найти все кратные числа диапазоне от 1 до 100, где множитель равен 5.

1. Начинаем с первого числа в диапазоне, то есть с числа 1.
2. Проверяем, делится ли число на множитель без остатка. В данном случае, проверяем, делится ли 1 на 5. Ответ: нет.
3. Переходим к следующему числу в диапазоне, то есть к числу 2.
4. Проверяем, делится ли число на множитель без остатка. В данном случае, проверяем, делится ли 2 на 5. Ответ: нет.
5. Продолжаем этот процесс для всех чисел в диапазоне.
6. Когда мы достигаем числа, которое делится на множитель без остатка, мы записываем его как кратное число.
7. Продолжаем проверять оставшиеся числа в диапазоне.
8. В результате, мы получим все кратные числа в заданном диапазоне.

В нашем примере с диапазоном от 1 до 100 и множителем 5, мы получим следующие кратные числа: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100.

Таким образом, чтобы найти все кратные числа в заданном диапазоне, нужно последовательно проверять каждое число в диапазоне на деление на множитель без остатка.

Примеры кратных чисел в математике

Вот некоторые примеры кратных чисел:

• Число 15 кратно числу 3 и числу 5, так как оно делится на оба числа без остатка.
• Число 20 кратно числу 4 и числу 5, так как оно делится на оба числа без остатка.
• Число 30 кратно числу 6 и числу 10, так как оно делится на оба числа без остатка.

Кратные числа в математике имеют важное значение при решении различных задач и упрощении вычислений.

Задачи на определение кратности чисел

Для определения кратности чисел можно использовать различные способы. Например, для определения кратности числа 7 числу 35, можно просто разделить число 35 на число 7. Если деление происходит без остатка, то число 35 кратно числу 7.

Другой способ определения кратности чисел заключается в проверке последней цифры числа. Если последняя цифра числа делится на заданное число без остатка, то число кратно этому заданному числу.

Определение кратности чисел имеет множество применений, в том числе в арифметических операциях, работе с дробями, алгебре и геометрии.

Пример 1:

Определить, кратно ли число 25 числу 5.

Для определения кратности чисел, нужно разделить число 25 на число 5.

25 ÷ 5 = 5

Результат деления без остатка, значит число 25 кратно числу 5.

Пример 2:

Определить, кратно ли число 63 числу 9.

Для определения кратности чисел, нужно разделить число 63 на число 9.

63 ÷ 9 = 7

Результат деления без остатка, значит число 63 кратно числу 9.

Пример 3:

Определить, кратно ли число 48 числу 4.

Для определения кратности чисел, нужно разделить число 48 на число 4.

48 ÷ 4 = 12

Результат деления без остатка, значит число 48 кратно числу 4.

Задачи на определение кратности чисел часто встречаются в математике и могут помочь укрепить понимание этого понятия и развить навыки работы с числами.

Видео по теме:

Вопрос-ответ:

Что такое кратное числа?

Кратное число — это число, которое делится на другое число без остатка. Например, число 10 является кратным числу 5, потому что оно делится на 5 без остатка.

Как найти кратное число?

Чтобы найти кратное число, нужно умножить это число на любое целое число. Например, чтобы найти кратное числу 5, мы можем умножить 5 на 2, получив 10.

Как проверить, является ли число кратным 5?

Чтобы проверить, является ли число кратным 5, нужно посмотреть на его последнюю цифру. Если последняя цифра числа равна 0 или 5, то число кратно 5. Например, число 35 кратно 5, так как его последняя цифра равна 5.

Какие числа являются кратными 5?

Числа, у которых последняя цифра равна 0 или 5, являются кратными 5. Например, 10, 25, 30, 45 и так далее.

Можно ли узнать, кратно ли число 5 без деления?

Да, можно узнать, кратно ли число 5 без деления, посмотрев на его последнюю цифру. Если последняя цифра числа является 0 или 5, то число кратно 5.

Что такое кратное в математике?

Кратное – это число, которое делится на другое число без остатка. Например, 10 кратно 5, потому что при делении 10 на 5 получается целое число (2).

Значение кратных чисел в повседневной жизни

Кратные числа играют важную роль в повседневной жизни и применяются в различных сферах. Они помогают нам организовать и систематизировать множество объектов или явлений.

Например, кратные числа часто используются в торговле и финансовом секторе. Банковские операции, такие как расчет процентов, выплаты зарплаты или пенсии, часто основываются на кратных числах. Это позволяет систематизировать и упростить финансовые операции.

В производственной сфере кратные числа используются для планирования и организации процессов. Например, при производстве товаров или услуг, кратные числа могут определять оптимальное количество единиц продукции, которое необходимо произвести или продать.

Кратные числа также имеют значение в науке и технике. В физике, математике и других научных дисциплинах кратные числа часто используются для моделирования и представления различных явлений и закономерностей.

В заключение, кратные числа являются важным инструментом для организации и систематизации объектов и явлений в повседневной жизни. Они применяются в различных сферах, таких как торговля, финансы, производство, наука и техника, и помогают нам упростить и оптимизировать различные процессы.

Практические задания для закрепления изученного материала

1. Найдите все кратные числа 5 в диапазоне от 0 до 50.

2. Напишите программу, которая будет выводить все кратные числа 5 в диапазоне, заданном пользователем.

3. Проверьте, являются ли следующие числа кратными 5: 15, 20, 25, 30.

4. Найдите наименьшее пятизначное число, которое делится на 5.

5. Какое наименьшее число, кратное 5, можно получить, составляя цифры числа 428?

6. Найдите сумму всех кратных чисел 5 в диапазоне от 100 до 200.

7. Найдите произведение всех кратных чисел 5 в диапазоне от 1 до 10.

8. Найдите среднее арифметическое всех кратных чисел 5 в диапазоне от 1 до 100.

9. Сколько существует пятизначных чисел, которые делятся на 5?

10. Найдите сумму всех пятизначных чисел, которые делятся на 5 и заканчиваются на 0.