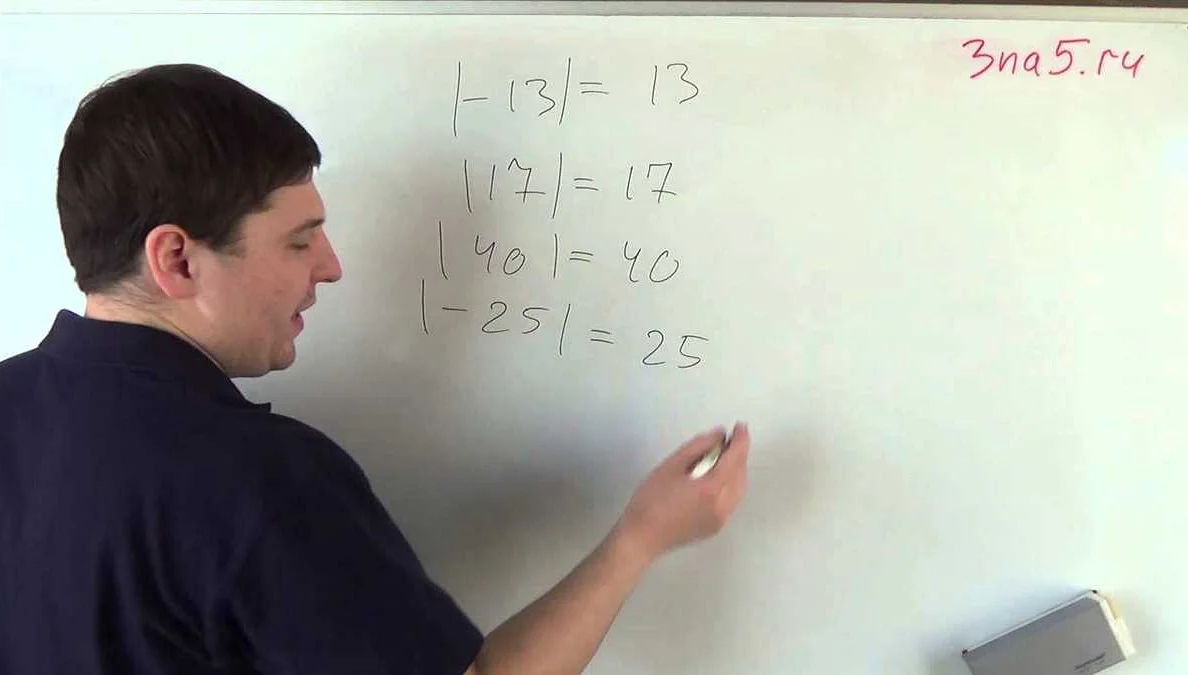Модуль что это такое в математике 6 класс
Содержимое
Модуль в математике для 6 класса — это понятие, которое помогает измерять расстояние между двумя числами или значениями. Узнайте, как работать с модулем и решать задачи с его использованием в 6 классе математики.
Модуль – одно из важнейших понятий в математике, которое изучается в шестом классе. Модулем числа называется его абсолютная величина, то есть расстояние от нуля на числовой оси. Модуль числа обозначается знаком | |, например |7| равно 7, а |-4| равно 4. Понимание модуля числа позволяет решать множество задач и упрощать математические выражения.
Определение модуля числа – это первый шаг для изучения его правил расчета. Правила расчета модуля позволяют определить его значение в зависимости от знака числа. Если число положительное, его модуль равен самому числу. Если число отрицательное, его модуль равен противоположному числу. Например, модуль числа -8 равен 8. Эти правила помогают упрощать выражения и решать задачи, связанные с модулем числа.
Пример задачи: найти модуль числа -12.
Для решения данной задачи следует использовать правило расчета модуля числа. Поскольку число -12 отрицательное, его модуль равен противоположному числу, то есть 12. Таким образом, модуль числа -12 равен 12.
Что такое модуль?
Правило определения модуля числа: если число положительное или равно нулю, то его модуль равен самому числу. Если число отрицательное, то его модуль равен числу с обратным знаком.
Например, модуль числа 5 равен 5, модуль числа -5 также равен 5.
Модуль числа может быть использован для определения расстояния между двумя точками на числовой прямой или для нахождения ошибки в измерениях.
Правила расчета модуля числа:
- Если число положительное или равно нулю, то его модуль равен самому числу: |x| = x.
- Если число отрицательное, то его модуль равен числу с обратным знаком: |x| = -x.
Примеры задач:
- Найдите модуль числа -7.
- Вычислите модуль числа 0.
Правила расчета модуля
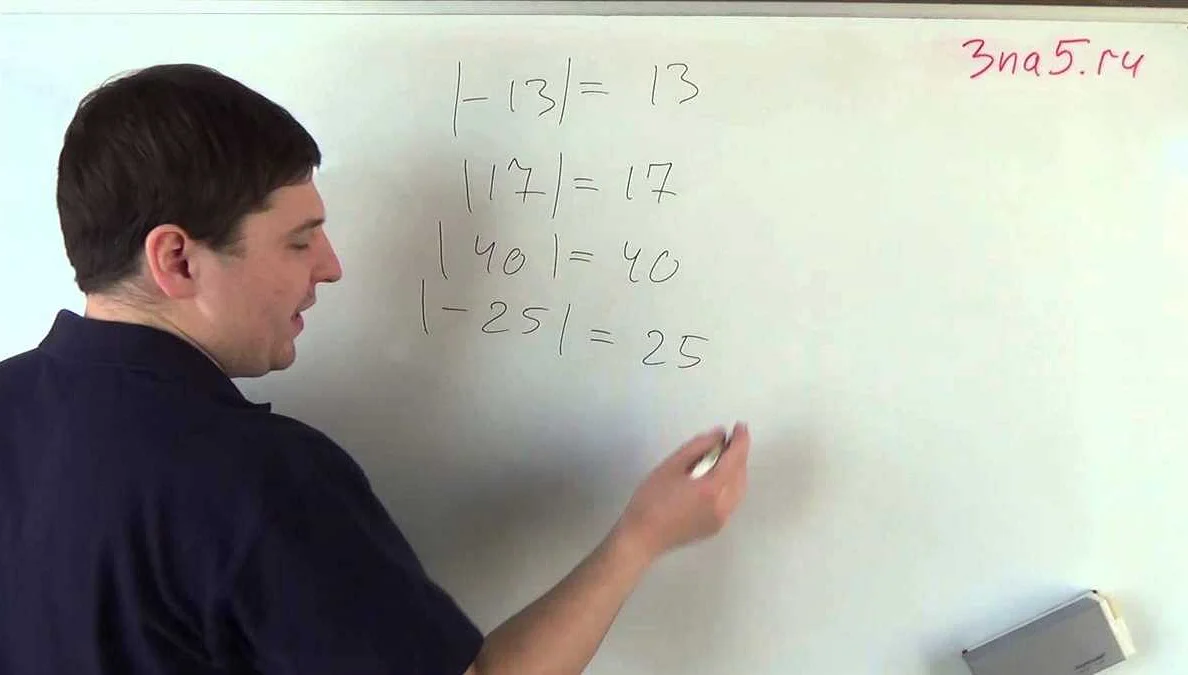
Правило 1: Модуль положительного числа равен самому числу.
Например, |5| = 5, |12| = 12.
Правило 2: Модуль отрицательного числа равен его противоположному числу.
Например, |-5| = 5, |-12| = 12.
Правило 3: Модуль нуля равен нулю.
Например, |0| = 0.
Правила расчета модуля помогают нам находить абсолютное значение чисел и использовать их в различных математических задачах. Знание этих правил позволяет нам корректно выполнять операции с модулями чисел.
Модуль в выражениях и уравнениях
Модуль числа представляет собой его абсолютное значение и обозначается символом | |. Он позволяет найти расстояние от данного числа до нуля на числовой прямой.
В выражениях модуль может использоваться для определения расстояния между двумя числами или для нахождения значения выражения с учетом абсолютного значения.
В уравнениях модуль может использоваться для нахождения всех возможных значений переменной, удовлетворяющих заданному условию.
Правила расчета с модулем в выражениях:
- Если число в модуле положительное или ноль, то модуль равен самому числу: |x| = x.
- Если число в модуле отрицательное, то модуль равен числу с обратным знаком: |x| = -x.
- Модуль суммы двух чисел равен сумме модулей этих чисел: |x + y| = |x| + |y|.
- Модуль разности двух чисел равен разности модулей этих чисел: |x — y| = |x| — |y|.
- Модуль произведения двух чисел равен произведению модулей этих чисел: |x * y| = |x| * |y|.
- Модуль частного двух чисел равен частному модулей этих чисел: |x / y| = |x| / |y| (при y ≠ 0).
Примеры задач:
1. Вычислите значение выражения |3 + 7|.
Решение: |3 + 7| = |10| = 10.
2. Найдите все значения переменной x, удовлетворяющие уравнению |2x — 5| = 7.
Решение: Рассмотрим два случая:
а) 2x — 5 = 7. Решая уравнение, получаем x = 6.
б) -(2x — 5) = 7. Решая уравнение, получаем x = -1.
Ответ: x = 6 или x = -1.
3. Найдите значение выражения |4 — 8| * 3.
Решение: |4 — 8| * 3 = |-4| * 3 = 4 * 3 = 12.
4. Найдите значение выражения |12 / 3| — |5 — 7|.
Решение: |12 / 3| — |5 — 7| = |4| — |-2| = 4 — 2 = 2.
Таким образом, понимание модуля числа и его использование в выражениях и уравнениях позволяет решать разнообразные задачи, связанные с абсолютным значением числа и его расстоянием на числовой прямой.
Модуль и неравенства
Модулем числа называется его абсолютная величина, то есть расстояние от нуля до этого числа на числовой прямой. Модуль числа обозначается символом | |. Например, модуль числа -5 обозначается как |-5| и равен 5.
Модуль числа неотрицательный, то есть он всегда больше или равен нулю. Это свойство модуля помогает в решении неравенств.
Рассмотрим неравенство с модулем:
- Если |а| < b, то значит а находится в пределах от -b до b, не включая границы. Например, если |х| < 3, то х находится в пределах от -3 до 3, не включая -3 и 3.
- Если |а| > b, то значит а находится за пределами от -b до b. Например, если |х| > 5, то х находится за пределами от -5 до 5.
- Если |а| ≤ b, то значит а находится в пределах от -b до b, включая границы. Например, если |х| ≤ 2, то х находится в пределах от -2 до 2, включая -2 и 2.
- Если |а| ≥ b, то значит а находится за пределами от -b до b, включая границы. Например, если |х| ≥ 4, то х находится за пределами от -4 до 4, включая -4 и 4.
Зная эти правила, можно решать различные задачи, содержащие неравенства с модулем.
Например, решим неравенство |2х — 3| < 5:
- Разбиваем неравенство на два варианта: 2х — 3 < 5 и -(2х — 3) < 5.
- Решаем каждое из полученных уравнений: для первого получаем 2х < 8, а для второго -2х < 2.
- Делаем вывод: 2х < 8, значит х < 4, и -2х < 2, значит х > -1.
- Соединяем полученные выводы: -1 < х < 4.
Таким образом, решением данного неравенства является интервал -1 < х < 4.
Примеры задач на расчет модуля

1. Найти модуль числа -7.
Решение: Модуль числа -7 равен 7, так как модуль числа это его абсолютное значение.
2. Найти модуль числа 0.
Решение: Модуль числа 0 равен 0, так как модуль числа это его абсолютное значение.
3. Найти модуль числа 9.
Решение: Модуль числа 9 равен 9, так как модуль числа это его абсолютное значение.
4. Найти модуль числа -12.
Решение: Модуль числа -12 равен 12, так как модуль числа это его абсолютное значение.
5. Найти модуль числа 5.
Решение: Модуль числа 5 равен 5, так как модуль числа это его абсолютное значение.
Свойства модуля

Основные свойства модуля:
- Модуль числа всегда неотрицателен: |a| ≥ 0, где а — произвольное число.
- Модуль числа равен нулю только в случае, когда само число равно нулю: |a| = 0 ⇔ a = 0.
- Модуль суммы двух чисел равен сумме модулей этих чисел: |a + b| = |a| + |b|.
- Модуль разности двух чисел равен разности модулей этих чисел: |a — b| = |a| — |b|.
- Модуль произведения двух чисел равен произведению модулей этих чисел: |a * b| = |a| * |b|.
- Модуль частного двух чисел равен частному модулей этих чисел: |a / b| = |a| / |b|.
- Если модуль числа меньше или равен нулю, то само число может быть равно нулю или быть отрицательным числом: |a| ≤ 0 ⇔ a ≤ 0.
Знание этих свойств помогает в решении задач на модуль и упрощает вычисления с модулем числа.
График модуля
График модуля функции представляет собой графическое изображение изменения значения модуля функции в зависимости от ее аргумента. Для построения графика модуля функции необходимо определить значения модуля для различных значений аргумента и отобразить их на координатной плоскости.
График модуля функции имеет некоторые особенности. Например, график модуля любой функции всегда находится выше или на одном уровне с осью OX. Это происходит потому, что модуль функции всегда принимает положительное значение или равен нулю.
Для построения графика модуля функции можно использовать таблицу значений, а также знания о свойствах модуля функции. Например, если известен график функции, можно построить график модуля, заменяя отрицательные значения функции их положительными аналогами.
Пример задачи, в которой необходимо построить график модуля функции, может выглядеть так:
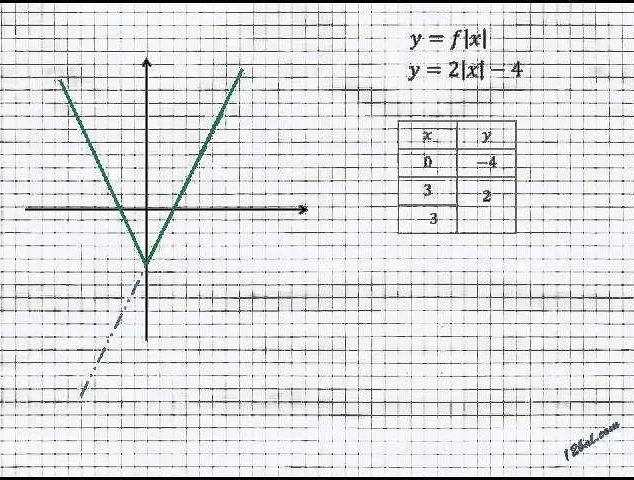
- Построить график модуля функции y = |x — 2|
Для решения данной задачи необходимо определить значения модуля функции для различных значений аргумента. Подставляя значения аргумента в функцию, получаем:
- При x = 0: y = |0 — 2| = 2
- При x = 1: y = |1 — 2| = 1
- При x = 2: y = |2 — 2| = 0
- При x = 3: y = |3 — 2| = 1
- При x = 4: y = |4 — 2| = 2
Подставив значения в таблицу, можно построить график модуля функции y = |x — 2|. На координатной плоскости будут отмечены точки с координатами (0, 2), (1, 1), (2, 0), (3, 1) и (4, 2), а затем их соединят прямыми линиями. Получится график модуля функции.
Применение модуля в реальной жизни
Например, модуль используется в задачах о скорости движения тела. Если нам известна скорость тела, но неизвестно, в какую сторону оно движется (положительное или отрицательное направление), то мы можем использовать модуль числа скорости, чтобы получить абсолютное значение скорости.
Также модуль применяется в задачах экономики, связанных с доходами и расходами. Например, если мы хотим узнать, насколько отличается наш зарплата от средней зарплаты в регионе, мы можем использовать модуль разности чисел.
В геометрии модуль используется для определения расстояния между двумя точками на плоскости. Если у нас есть координаты двух точек, то мы можем использовать модуль разности координат, чтобы получить расстояние между ними.
Таким образом, модуль является важным инструментом для работы с абсолютными значениями и находит широкое применение в различных областях реальной жизни.
Видео по теме:
Что такое модуль в математике?
Модуль числа — это выражение, которое показывает абсолютное значение числа, то есть его удаление от нуля. Например, модуль числа -5 равен 5, а модуль числа 3 равен 3. Модуль числа можно обозначить двойными вертикальными чертами: |x|.
Как вычислить модуль числа?
Для вычисления модуля числа нужно проверить его значение. Если число положительное или равно нулю, то модуль будет равен самому числу. Если число отрицательное, то модуль равен этому числу с обратным знаком. Например, модуль числа -7 равен 7, а модуль числа 4 равен 4.
Какие правила расчета модулей чисел?
В математике существуют несколько правил для расчета модулей чисел. Например, модуль суммы двух чисел равен сумме модулей этих чисел. Модуль произведения двух чисел равен произведению модулей этих чисел. Если нужно вычислить модуль разности двух чисел, то нужно вычесть из модуля первого числа модуль второго числа. Например, модуль суммы чисел 5 и 3 равен 8, модуль произведения чисел 4 и 6 равен 24, а модуль разности чисел 9 и 2 равен 7.