Что такое модуль числа в математике 6 класс определение с примерами
Содержимое
- 1 Что такое модуль числа в математике 6 класс определение с примерами
Модуль числа — абсолютное значение числа, в математике это означает, что мы игнорируем его знак. В 6 классе учатся определять модуль числа и решать задачи с его использованием. В данной статье приведены определение модуля числа и примеры его применения.
Модуль числа – это понятие, которое обозначает расстояние от числа до нуля на числовой прямой. Он всегда является положительным числом или нулем. Модуль числа обозначается символом | |. Например, модуль числа -3 записывается как |-3| и равен 3, так как расстояние от -3 до нуля равно 3.
Модуль числа можно определить с помощью следующих правил:
- Если число положительное или ноль, то его модуль равен самому числу. Например: |5| = 5, |0| = 0.
- Если число отрицательное, то его модуль равен числу с обратным знаком. Например: |-5| = 5, |-3| = 3.
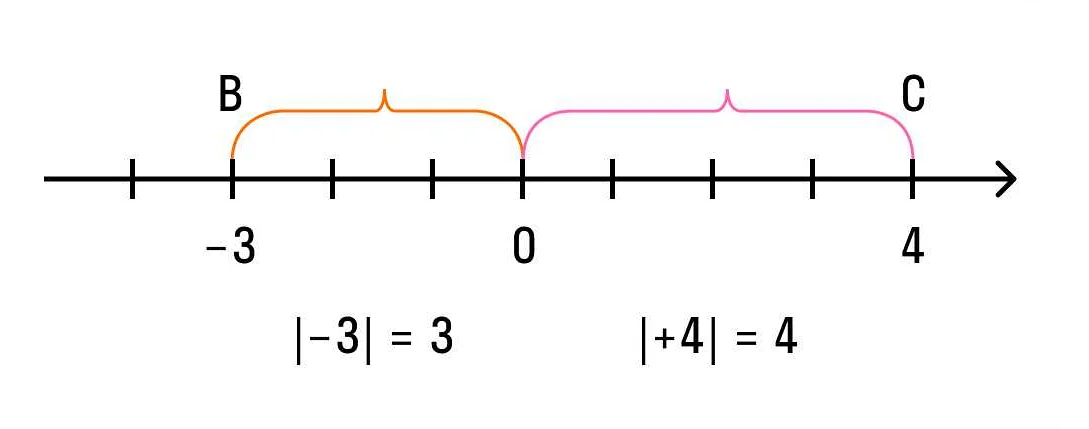
Модуль числа может быть использован в различных математических задачах. Например, при нахождении расстояния между двумя точками на числовой прямой, модуль числа позволяет получить положительное значение расстояния, независимо от того, какие числа используются.
Модуль числа в математике 6 класс
Модуль числа всегда является неотрицательным. Если число положительное, то модуль числа равен самому числу. Например, |5| = 5. Если число отрицательное, то модуль числа равен этому числу с обратным знаком. Например, |-5| = 5.
Модуль числа можно представить в виде таблицы:
Число xМодуль |x|
| +5 | 5 |
| +3 | 3 |
| 0 | 0 |
| -3 | 3 |
| -5 | 5 |
Таким образом, модуль числа позволяет нам получить абсолютное значение числа, игнорируя его знак. Он широко используется в различных областях математики и физики для решения задач и выражения различных величин.
Видео по теме:
Определение модуля числа

Модулем числа называется неотрицательное значение этого числа. Другими словами, модуль числа показывает, насколько далеко это число находится от нуля на числовой оси.
Модуль числа обозначается символом |a|, где a — число. Если a положительное, то |a| = a. Если a отрицательное, то |a| = -a.
Например, модуль числа 5 равен 5, так как 5 находится на пяти шагах от нуля в положительном направлении. Модуль числа -3 равен 3, так как -3 находится на трех шагах от нуля в отрицательном направлении.
Модуль числа можно использовать для вычисления расстояния между двумя точками на числовой оси или для нахождения значения выражений, содержащих арифметические операции с модулем числа.
Правила определения модуля числа
Правила определения модуля числа:
- Если число a неотрицательное (a ≥ 0), то модуль числа равен самому числу: |a| = a.
- Если число a отрицательное (a < 0), то модуль числа равен числу с обратным знаком: |a| = -a.
Например, модуль числа 5 равен 5, так как число 5 неотрицательное. Модуль числа -5 равен 5, так как число -5 отрицательное и его модуль равен числу с обратным знаком.
Модуль числа может быть использован, например, для определения расстояния между двумя точками на числовой прямой или для нахождения модуля разности двух чисел.
Вопрос-ответ:
Что такое модуль числа?
Модуль числа — это значение, которое показывает, насколько число отличается от нуля. Модуль числа всегда является неотрицательным числом.
Как определить модуль числа?
Модуль числа можно определить следующим образом: если число положительное, то модуль равен самому числу, если число отрицательное, то модуль равен числу с обратным знаком.
Как можно использовать модуль числа в математике?
Модуль числа часто используется для определения расстояния между двумя точками на числовой оси. Он также может использоваться для нахождения абсолютной величины разности двух чисел.
Какие примеры можно привести для понимания модуля числа?
Примеры использования модуля числа: модуль числа 5 равен 5, модуль числа -3 равен 3, модуль числа 0 равен 0.
Какие свойства имеет модуль числа?
Модуль числа обладает следующими свойствами: модуль суммы двух чисел равен сумме модулей этих чисел, модуль разности двух чисел равен модулю их разности, модуль произведения двух чисел равен произведению модулей этих чисел.
Вычисление модуля числа

Для вычисления модуля числа используется следующая формула:
|x| = x, если x ≥ 0
|x| = -x, если x < 0
Например, модуль числа -5 будет равен 5, так как -5 < 0. А модуль числа 3 будет равен 3, так как 3 ≥ 0.
Вычисление модуля числа может быть полезно при работе с различными задачами и уравнениями, так как позволяет игнорировать знак числа и сосредоточиться только на его абсолютной величине.
Свойства модуля числа
Если a – это число, то |a| = a, если a ≥ 0, и |a| = -a, если a < 0.
Модуль числа обладает следующими свойствами:
- Модуль неотрицательного числа равен самому числу: |a| = a, если a ≥ 0.
- Модуль отрицательного числа равен противоположному числу: |a| = -a, если a < 0.
- Модуль нуля равен нулю: |0| = 0.
- Модуль суммы двух чисел равен сумме модулей этих чисел: |a + b| = |a| + |b|.
- Модуль разности двух чисел равен разности модулей этих чисел: |a — b| = |a| — |b|.
- Модуль произведения двух чисел равен произведению модулей этих чисел: |a * b| = |a| * |b|.
Эти свойства модуля числа позволяют упростить вычисления и решать различные задачи, связанные с алгеброй и геометрией.
Примеры вычисления модуля чисел
Модуль числа можно вычислить с помощью математической формулы:
|x| = x, если x ≥ 0
|x| = -x, если x < 0
Ниже приведены примеры вычисления модуля чисел:
ЧислоМодуль
| -5 | 5 |
| 0 | 0 |
| 7 | 7 |
| -2 | 2 |
Модуль отрицательного числа
Чтобы найти модуль отрицательного числа, необходимо удалить знак минус и оставить только значение числа. Это можно сделать, просто убрав знак минус перед числом. Модуль отрицательного числа всегда будет положительным числом.
Ниже приведена таблица с примерами вычисления модуля отрицательных чисел:
Отрицательное числоМодуль
| -2 | 2 |
| -7 | 7 |
| -12 | 12 |
Таким образом, модуль отрицательного числа всегда будет положительным числом, равным абсолютной величине этого числа.
Модуль положительного числа

Например, модуль числа 5 равен 5, так как оно положительное.
Модуль числа можно обозначить символом |x|, где x — число, модуль которого нужно найти.
Модуль положительного числа можно представить в виде следующей формулы:
|x| = x, если x ≥ 0
Например, |5| = 5, |10| = 10, |100| = 100 и т.д.
Модуль положительного числа может использоваться в различных задачах, например, для определения расстояния между двумя точками на числовой оси или для нахождения значения выражения при заданных значениях переменных.



Модуль числа в математике очень полезная и интересная тема для изучения. Я рад, что в 6 классе мы начали узнавать об этом понятии. Модуль числа — это абсолютное значение числа, то есть его числовая величина без учета знака. Например, модуль числа -5 будет равен 5, а модуль числа 3 останется равным 3. Модуль числа может быть полезным при решении различных задач. Например, если нам нужно найти расстояние между двумя точками на числовой оси, мы можем использовать модуль числа, чтобы найти абсолютное значение этого расстояния. Также модуль числа может помочь нам определить, какое из двух чисел больше. Если модуль одного числа больше модуля другого, то это означает, что первое число больше второго по абсолютной величине. В общем, модуль числа — это очень важное понятие в математике, которое помогает нам работать с числами и решать различные задачи. Я уверен, что с помощью примеров и практических задач мы сможем лучше понять и усвоить это понятие.
Мне очень понравилась данная статья о модуле числа в математике. Она ясно и доступно объясняет понятие модуля, что особенно важно для учеников 6 класса. Я теперь точно понимаю, что модуль числа — это его расстояние от нуля на числовой прямой. Примеры, приведенные в статье, помогли мне лучше усвоить материал. Теперь я могу легко определить модуль числа и решить задачи, связанные с этой темой. Большое спасибо автору за информативную статью! Я надеюсь, что в будущем будут еще такие интересные материалы для обучения математике.