Что значит двойной модуль в математике

Двойной модуль в математике – это математическая операция, которая позволяет выразить расстояние между двумя числами, независимо от их знака. Узнайте, как использовать двойной модуль и для чего он может быть полезен.

Двойной модуль — это математическое понятие, которое используется для определения расстояния между двумя точками на числовой прямой. Он представляет собой числовое значение, которое всегда положительно или равно нулю. Двойной модуль обозначается двумя вертикальными чертами, которые окружают число или выражение.

Двойной модуль может быть использован для нахождения расстояния между двумя точками на числовой прямой или для определения значений функций, которые могут быть положительными или отрицательными в зависимости от аргумента. Например, если есть функция, которая может принимать как положительные, так и отрицательные значения, то двойной модуль может быть использован для получения значения функции в абсолютном значении.

Например, для функции f(x) = |x — 5| двойной модуль используется для того, чтобы получить значение функции в абсолютном значении независимо от того, является ли аргумент положительным или отрицательным. Если x = 3, то f(x) = |3 — 5| = |-2| = 2. Если x = 7, то f(x) = |7 — 5| = |2| = 2.

Таким образом, двойной модуль является полезным математическим инструментом, который позволяет определить расстояние между двумя точками на числовой прямой и получить значения функций в абсолютном значении. Он широко используется в различных областях математики, физики и других наук.

Общая информация о двойном модуле

В математике двойной модуль используется для вычисления абсолютной величины некоторого числа или выражения. Он представляет собой операцию, которая возвращает неотрицательное значение, независимо от знака исходного числа или выражения.

Двойный модуль может быть выражен следующим образом:

• Если число или выражение положительное, то двойной модуль равен самому числу или выражению.
• Если число или выражение отрицательное, то двойной модуль равен числу или выражению с обратным знаком.

Например, двойной модуль числа -5 равен 5, а двойной модуль выражения -2x равен 2x.

Двойной модуль широко используется в различных областях математики, включая алгебру, геометрию и математический анализ. Он может быть полезен при решении уравнений, нахождении максимального или минимального значения функции, а также при работе с комплексными числами.

Определение и свойства двойного модуля

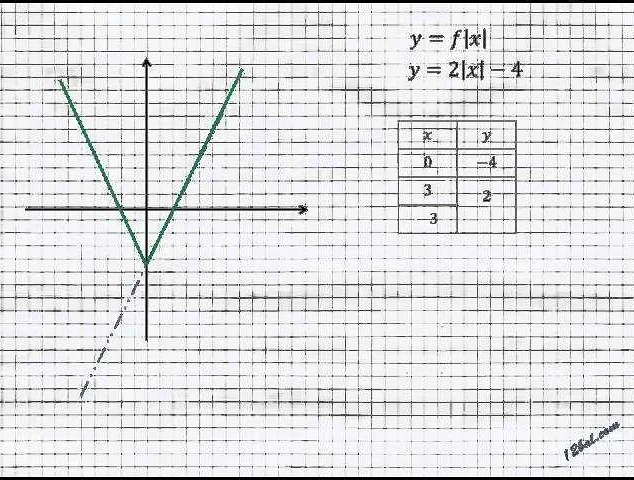
Для любого действительного числа x двойной модуль обозначается как ||x|| и определяется следующим образом:

Если x ≥ 0, то ||x|| = x.

Если x < 0, то ||x|| = -x.

То есть двойной модуль числа показывает расстояние от числа до нуля на числовой прямой, игнорируя его знак.

Свойства двойного модуля:

1. ||x|| ≥ 0 для любого числа x.
2. Если x = 0, то ||x|| = 0.
3. Если x ≠ 0, то ||x|| > 0.
4. ||x * y|| = ||x|| * ||y|| для любых чисел x и y.
5. ||x + y|| ≤ ||x|| + ||y|| для любых чисел x и y (неравенство треугольника).

Двойной модуль используется в различных областях математики, физики, экономики и других науках для нахождения расстояний, определения нормы и модуля числа и других задач.

Примеры использования двойного модуля

Двойной модуль часто используется в математике и физике для решения различных задач. Рассмотрим несколько примеров его применения:

1. Расстояние между двумя точками на координатной плоскости. Пусть даны две точки A(x1, y1) и B(x2, y2). Расстояние между этими точками можно вычислить с помощью формулы:

d = ||AB|| = sqrt((x2 — x1)^2 + (y2 — y1)^2)

Здесь двойной модуль используется для того, чтобы учесть возможное отрицательное значение разности координат.

2. Решение системы уравнений. При решении системы уравнений методом Гаусса-Жордана, двойной модуль может быть использован для приведения системы к треугольному виду. Это позволяет удобно находить решение системы.

3. Определение расстояния от точки до прямой. Пусть дана прямая Ax + By + C = 0 и точка P(x0, y0). Расстояние от точки P до прямой можно вычислить с помощью формулы:

d = ||Ax0 + By0 + C|| / sqrt(A^2 + B^2)

Здесь двойной модуль используется для того, чтобы учесть возможное отрицательное значение Ax0 + By0 + C.

Это лишь некоторые примеры использования двойного модуля в математике. Он также широко применяется в физике, экономике и других науках для решения различных задач.

Двойной модуль в комплексных числах

Комплексное число представляет собой числовую величину, которая состоит из действительной и мнимой частей. Обычно комплексное число записывается в виде z = a + bi, где a — действительная часть, b — мнимая часть, а i — мнимая единица.

Для вычисления двойного модуля комплексного числа z = a + bi используется следующая формула:

|z| = |a + bi| = √(a^2 + b^2)

Таким образом, двойной модуль комплексного числа — это квадратный корень из суммы квадратов его действительной и мнимой частей.

Пример:

Дано комплексное число z = 3 + 4i. Чтобы найти его двойной модуль, нужно вычислить √(3^2 + 4^2) = √(9 + 16) = √25 = 5.

Таким образом, двойной модуль комплексного числа z = 3 + 4i равен 5.

Двойной модуль в комплексных числах может использоваться для решения различных задач, таких как нахождение расстояния между точками на комплексной плоскости или определение радиуса круга с центром в начале координат.

Двойной модуль в векторном пространстве

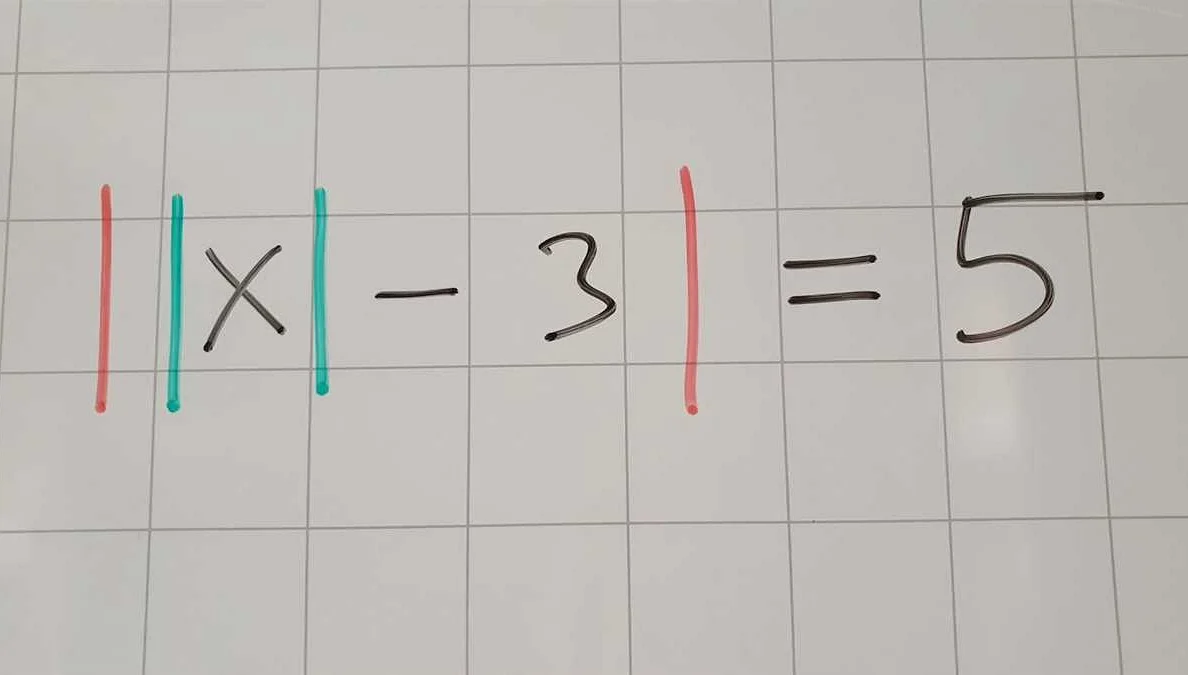
Двойной модуль вектора является одним из способов выражения абсолютной величины вектора. В отличие от обычного модуля, который всегда является неотрицательным числом, двойной модуль может быть положительным или отрицательным.

Для вектора v в векторном пространстве, двойной модуль определяется следующим образом:

|v| = |v|, если v неотрицательный вектор

|v| = -|v|, если v отрицательный вектор

Пример использования двойного модуля в векторном пространстве:

Пусть есть вектор v = (2, -3, 5). Его двойной модуль будет равен |v| = -|(2, -3, 5)| = -(2 + |-3| + 5) = -(2 + 3 + 5) = -10.

Таким образом, двойной модуль вектора v равен -10.

Видео по теме:

Вопрос-ответ:

Что такое двойной модуль в математике?

Двойной модуль — это математическая операция, которая применяется к числу или выражению и возвращает их абсолютное значение, независимо от знака. Если число или выражение положительное, то двойной модуль равен исходному числу или выражению. Если число или выражение отрицательное, то двойной модуль равен числу или выражению с обратным знаком.

Как используется двойной модуль в математике?

Двойной модуль возможно использовать в различных ситуациях. Одно из применений — это нахождение расстояния между двумя точками на числовой оси. Для этого необходимо вычислить разность координат точек и взять двойной модуль этой разности. Другое применение — это решение уравнений или неравенств, включающих модули. Двойной модуль позволяет убрать модуль и рассмотреть два возможных значения переменной или выражения, одно со знаком плюс, другое со знаком минус.

Каковы особенности использования двойного модуля в математике?

Одной из особенностей использования двойного модуля является то, что он всегда возвращает неотрицательное значение. Это связано с тем, что двойной модуль отрицательного числа равен числу с обратным знаком, который уже является неотрицательным. Еще одна особенность — это то, что двойной модуль может применяться к числам, выражениям и функциям.

Какие примеры использования двойного модуля в математике вы можете привести?

Один из примеров использования двойного модуля — это нахождение расстояния между двумя точками на числовой оси. Если координаты точек равны x1 и x2, то расстояние равно двойному модулю разности x2 — x1. Еще один пример — это решение уравнений или неравенств с модулями. Например, чтобы решить уравнение |x — 3| = 5, можно воспользоваться свойством двойного модуля и записать два возможных уравнения: x — 3 = 5 и x — 3 = -5. Затем решить каждое из них и получить два значения переменной x.

Применение двойного модуля в теории вероятностей

Двойной модуль может быть полезным инструментом в теории вероятностей для работы с различными случайными величинами. Он позволяет учитывать как положительные, так и отрицательные значения, что может быть важно при анализе вероятностных событий.

Одним из примеров применения двойного модуля в теории вероятностей является расчёт модуля разности двух случайных величин. Например, если у нас есть две случайные величины X и Y, то мы можем рассчитать модуль разности как |X — Y|. Это может быть полезно, например, при анализе разности результатов двух экспериментов или при сравнении двух наблюдаемых значений.

Еще одним примером применения двойного модуля в теории вероятностей является расчёт модуля разности между случайной величиной и её математическим ожиданием. Например, если у нас есть случайная величина X и её математическое ожидание E(X), то мы можем рассчитать модуль разности как |X — E(X)|. Это может помочь определить насколько случайная величина отклоняется от своего среднего значения и оценить вероятность такого отклонения.

Таким образом, двойной модуль в теории вероятностей может быть полезным инструментом для анализа различных случайных величин и оценки вероятностей различных событий.

Значение двойного модуля в алгебре

В алгебре двойной модуль используется для определения абсолютной величины числа или выражения. Он позволяет получить неотрицательное значение, независимо от знака числа или выражения.

Для числа x двойной модуль записывается как |x| и определяется следующим образом:

• Если x больше или равно нулю, то двойной модуль равен x: |x| = x
• Если x меньше нуля, то двойной модуль равен отрицательному значению x: |x| = -x

Применение двойного модуля в алгебре позволяет упростить выражения и решать уравнения. Например, двойной модуль может использоваться для нахождения расстояния между двумя точками на числовой оси.

Рассмотрим пример: пусть даны две точки A и B с координатами x1 и x2. Расстояние между этими точками можно найти как двойной модуль разности координат: |x1 — x2|. Если оба значения x1 и x2 положительные или оба отрицательные, то двойной модуль равен их разности. Если одно значение положительное, а другое отрицательное, то двойной модуль равен сумме их модулей.

Таким образом, использование двойного модуля в алгебре облегчает работу с абсолютными значениями и позволяет упростить вычисления и решение уравнений.