Что такое дифференциалы математика

Дифференциалы в математике — это инструмент для изучения степени изменения функций. Узнайте, как использовать дифференциалы для анализа функций, нахождения касательных и определения экстремумов.

Дифференциалы — это одно из ключевых понятий в области математического анализа. Они используются для изучения изменений функций при небольших изменениях их аргументов. Дифференциалы позволяют более точно определить, как функция меняется в каждой точке своей области определения.

Определение дифференциала включает в себя понятия производной и линейной аппроксимации. Дифференциал функции f(x) в точке x представляет собой линейную функцию, которая наилучшим образом приближает значения функции в окрестности этой точки. Он может быть представлен в виде f(x + dx) = f(x) + f'(x) · dx, где dx — малое изменение аргумента, а f'(x) — производная функции f(x) в точке x.

Пример использования дифференциалов — нахождение приближенных значений функций. Если известны значения функции и её производной в некоторой точке, то можно использовать дифференциалы для приближенного вычисления значений функции вблизи этой точки. Например, для приближенного вычисления значения синуса можно использовать разложение в ряд Тейлора и дифференциалы.

Применение дифференциалов распространено в различных областях, включая физику, экономику, инженерию и другие. Они позволяют описывать и анализировать изменения величин и функций в окрестности заданной точки. Дифференциалы также являются базовым инструментом для изучения дифференциальных уравнений, которые широко применяются в различных научных и технических областях.

Что такое дифференциалы в математике?

Дифференциалы обычно обозначаются символом «dx» и представляют собой бесконечно малый прирост аргумента функции. Они позволяют описывать, как изменяется значение функции при изменении аргумента на бесконечно малую величину. Дифференциалы позволяют точно выразить исчезающе малые изменения функции и позволяют аппроксимировать функцию линейными приращениями.

Применение дифференциалов в математике очень широко. Они используются для нахождения производных функций, определения экстремумов функций, исследования графиков функций, а также для решения задач физики, экономики, статистики и других наук. Дифференциалы также являются основой для дальнейшего изучения интегралов и интегрального исчисления.

Примеры использования дифференциалов включают нахождение производной функции y = x^2, где dx представляет бесконечно малый прирост аргумента x. Дифференциалы также используются для нахождения касательной к графику функции, аппроксимации функции линейным приближением, определения момента изменения функции и многих других задач.

Определение дифференциалов

Дифференциал функции f(x) обозначается как df(x) или dy и определяется следующим образом:

dx = х — x0

dy = f’(x0)dx

Здесь x — это независимая переменная, x0 — точка, в которой вычисляется дифференциал, f’(x0) — производная функции в точке x0, dx — изменение x, dy — соответствующее изменение y.

Дифференциалы широко используются в математическом анализе, дифференциальных уравнениях и физике. Они позволяют оценивать приращения функций и аппроксимировать изменения между точками.

Формула дифференциала

Формула дифференциала записывается следующим образом:

Если f(x) — функция, дифференцируемая в точке x, то дифференциал функции в точке x равен:

$$df = f'(x) \cdot dx$$

где f'(x) — производная функции f(x) в точке x, а dx — бесконечно малое изменение аргумента x.

Формула дифференциала позволяет вычислять производные функций и аппроксимировать небольшие изменения функции вблизи заданной точки.

Например, для функции f(x) = x^2, производная функции равна f'(x) = 2x. Таким образом, для точки x = 3 значение дифференциала будет:

$$df = f'(3) \cdot dx = 2 \cdot 3 \cdot dx = 6dx$$

Формула дифференциала имеет широкое применение в различных областях науки и техники, включая физику, экономику и инженерные расчеты.

Примеры использования дифференциалов

1. Приближенное вычисление функции

Одним из основных применений дифференциалов является приближенное вычисление значений функции. При использовании дифференциалов мы можем оценить прирост функции при изменении аргумента, что позволяет нам сделать приближенное предсказание значений функции вблизи заданной точки.

2. Линеаризация функции

Дифференциалы позволяют нам линеаризовать функции, то есть аппроксимировать их линейными функциями. Это удобно для анализа и работы с более сложными функциями, так как линейные функции легче исследовать и использовать для дальнейших вычислений.

3. Определение экстремумов функции

С помощью дифференциалов мы можем определить экстремумы функции, то есть ее максимумы и минимумы. Для этого достаточно найти точки, в которых дифференциал обращается в нуль.

4. Построение касательной к графику функции

Дифференциалы также используются для построения касательной линии к графику функции в заданной точке. Касательная линия позволяет нам локально приблизить график функции и аппроксимировать его поведение вблизи данной точки.

5. Вычисление погрешности и оценка точности приближений

Дифференциалы позволяют нам вычислять погрешность приближенных значений функции и оценивать точность самих приближений. Это особенно важно при проведении численных экспериментов и анализе результатов.

Описанные выше примеры являются лишь некоторыми из множества возможностей, которые предоставляют дифференциалы. Они позволяют нам более глубоко изучать и анализировать функции, а также делать более точные и надежные вычисления.

Дифференциалы в физике

В физике дифференциалы играют важную роль при решении задач, связанных с изменениями физических величин. Дифференциалы позволяют описать малые изменения величин и выразить их в виде дифференциального уравнения.

Дифференциалы часто используются при описании движения тела и изменения его скорости. Например, дифференциалы могут помочь определить мгновенное ускорение тела или изменение его положения в пространстве.

Также дифференциалы применяются при анализе электрических цепей и расчете тока. Они позволяют рассчитывать изменение напряжения и силы тока в зависимости от изменения сопротивления или других параметров цепи.

Дифференциалы используются и в других областях физики, таких как термодинамика, оптика, астрономия и др. Они помогают описать и предсказать изменения физических явлений и явления в окружающем мире.

В целом, дифференциалы являются мощным инструментом для анализа и моделирования физических процессов. Они позволяют описать и предсказать изменения различных величин и явлений, а также помогают решать сложные задачи в физике.

Применение дифференциалов в экономике

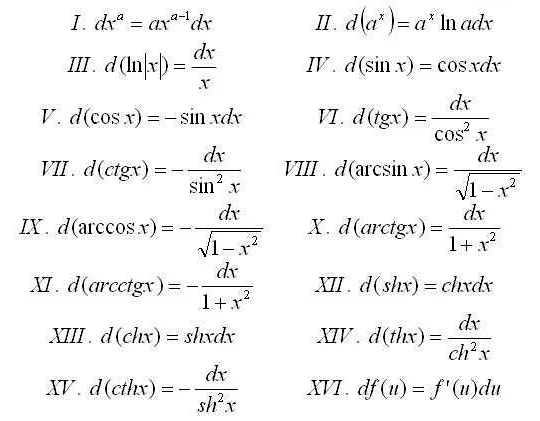
Дифференциалы играют важную роль в экономической теории и позволяют анализировать изменения в экономических переменных. Они используются для моделирования и предсказания поведения рынков, определения оптимальных стратегий, а также для измерения и оценки экономических величин.

Одним из основных применений дифференциалов в экономике является определение маржинальных изменений. Маржинальный изменение показывает, как изменится результат в ответ на небольшое изменение входных данных. Например, маржинальный доход позволяет определить, как изменится доход компании при увеличении объема продажи каждого дополнительного товара. Это важно для принятия решений о ценообразовании и оптимизации производства.

Дифференциалы также используются для определения эластичности спроса и предложения. Эластичность показывает, насколько сильно изменится спрос или предложение в ответ на изменение цены или других факторов. Это позволяет компаниям и правительствам прогнозировать изменения в рыночных условиях и адаптировать свои стратегии соответственно.

Дифференциалы также применяются в финансовой экономике для моделирования и оценки финансовых инструментов, таких как опционы, фьючерсы и деривативы. Они позволяют анализировать риски и доходность различных инвестиционных стратегий, а также прогнозировать изменения на финансовых рынках.

В общем, применение дифференциалов в экономике является неотъемлемой частью анализа и моделирования экономических процессов. Они позволяют более точно предсказывать и оценивать изменения в экономических переменных и принимать обоснованные решения в условиях неопределенности.

Дифференциалы в геометрии

Дифференциалы также играют важную роль в геометрии. В геометрии дифференциалы используются для описания изменений формы и размеров геометрических объектов.

Например, дифференциалы могут использоваться для расчета длины кривой, площади поверхности или объема тела. Дифференциалы позволяют представить эти геометрические величины как бесконечно малые приращения других величин.

Кроме того, дифференциалы используются для описания кривизны поверхности. Например, кривизна поверхности в каждой точке может быть представлена дифференциалом кривизны.

Дифференциалы также важны для понимания трансформаций геометрических объектов. Они позволяют определить, как изменяются координаты точек при преобразованиях, таких как вращение, масштабирование или сдвиг.

Выводы, сделанные с использованием дифференциалов в геометрии, могут быть применены в различных областях, включая компьютерную графику, компьютерное зрение, робототехнику и архитектуру.

Вопрос-ответ:

Что такое дифференциалы в математике?

В математике дифференциалы — это малые приращения функций, выраженные через дифференциальные коэффициенты.

Как можно объяснить понятие дифференциалов в математике?

Дифференциалы в математике — это инструмент, позволяющий изучать изменения функций и их приращения в определенной точке.

Можете привести примеры дифференциалов?

Конечно! Например, для функции f(x) = x^2, дифференциал dx будет равен 2x * dx. Также можно рассмотреть функцию f(x) = sin(x), и ее дифференциал dx будет равен cos(x) * dx.

В каких областях математики применяются дифференциалы?

Дифференциалы широко применяются в математическом анализе, физике, экономике и других науках. Они играют важную роль при исследовании функций, определении экстремумов и решении дифференциальных уравнений.

Метод дифференциалов в оптимизации

Для применения метода дифференциалов в оптимизации необходимо иметь функцию, которую требуется оптимизировать, и ограничения на значения ее аргументов. С помощью дифференциала функции можно оценить, как изменится значение функции при изменении каждого аргумента на некоторую величину.

Основным применением метода дифференциалов в оптимизации является поиск экстремумов функций. Экстремумы – это точки, в которых функция достигает наибольшего или наименьшего значения. С помощью метода дифференциалов можно найти точку, в которой функция достигает экстремума.

Для применения метода дифференциалов в оптимизации необходимо вычислить производные функции по каждому аргументу. Это позволяет определить направление изменения функции и найти точку, в которой функция достигает экстремума.

Метод дифференциалов широко применяется в различных областях, таких как экономика, физика, инженерия и многие другие. Он позволяет оптимизировать процессы и повысить эффективность систем, используя математические методы и техники анализа функций.

Видео по теме: