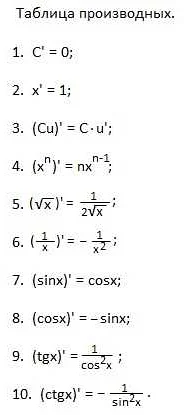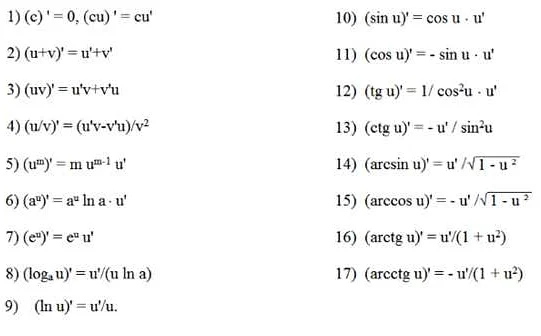Что означает штрих в математике в производной

Штрих в математике в производной обозначает производную функции по переменной в определенной точке. Узнайте, как использовать штрих в математических выражениях и понять его значение для производной.

Штрих – это символ, который в математике обозначает производную функции. Производная – это понятие, которое позволяет оценить скорость изменения функции в каждой точке её области определения. Штрих записывается после функции и указывает на то, что мы ищем производную этой функции. Важно понимать, что штрих не является самостоятельной математической операцией, а является лишь обозначением для производной.

Производная функции может быть представлена как отношение приращения значения функции к приращению аргумента функции, когда это приращение стремится к нулю. В других словах, производная функции показывает, как быстро функция меняется, когда аргумент функции меняется незначительно. Чтобы найти значение производной функции в определенной точке, необходимо использовать соответствующие правила дифференцирования и арифметические операции.

Например, рассмотрим функцию f(x) = x^2. Чтобы найти производную этой функции, мы можем использовать правило дифференцирования степенной функции. Применяя это правило, мы получим f'(x) = 2x. Таким образом, штрих после функции указывает на то, что мы дифференцируем функцию и ищем её производную.

В математике штрих может использоваться не только для обозначения производной функции, но и для обозначения производных высших порядков. Например, два штриха (f») после функции указывают на вторую производную функции, три штриха (f»’) – на третью производную, и так далее.

Что такое штрих в математике и зачем он нужен?

Штрих широко применяется в дифференциальном и интегральном исчислении, которые являются основными областями математики. Он позволяет нам исследовать изменение функции в зависимости от изменения ее аргумента и решать различные задачи, связанные с определением экстремумов функций, нахождением площадей и объемов фигур, а также моделированием различных процессов в физике, экономике и других науках.

Например, если у нас есть функция f(x), то ее производная обозначается как f'(x) или df/dx. Производная показывает, как быстро меняется значение функции f в данной точке x. Это может быть полезно при анализе графиков функций, определении траектории движения объектов, вычислении скорости изменения величин и многих других задачах.

Использование штриха в математике помогает нам более точно описывать и изучать различные явления и процессы, которые можно представить в виде математических моделей. Он позволяет нам вычислять и анализировать различные характеристики функций и получать полезные сведения о них.

Видео по теме:

Роль штриха в производной

Штрих обычно обозначается символом ‘ и ставится после обозначения функции. Например, если функция обозначается как f(x), то ее производная будет обозначаться как f'(x) или df/dx. Штрих может также указывать на число раз, которое нужно продифференцировать функцию. Например, если f»(x) — это вторая производная функции f(x), то f»'(x) — третья производная.

Штрих позволяет нам анализировать свойства функции и ее графика. Он показывает, как меняется наклон касательной к графику функции в каждой точке. Если производная положительна в точке, то функция возрастает в этой точке. Если производная отрицательна, то функция убывает. Если производная равна нулю, то функция достигает экстремума (максимума или минимума) в этой точке.

Штрих также позволяет нам находить точки перегиба графика функции. Точка перегиба — это точка, в которой меняется выпуклость графика (например, изогнутость вверх меняется на изогнутость вниз). Это происходит, когда вторая производная функции равна нулю или не существует.

Использование штриха в производной позволяет нам более глубоко изучать функции и их свойства. Это основной инструмент дифференциального исчисления, который находит широкое применение в математике, физике, экономике и других науках.

Объяснение штриха в математике

Производная функции определяется как предел отношения изменения функции к изменению ее аргумента при бесконечно малом приращении аргумента. Штрих функции можно представить как скорость роста или убывания функции.

Например, если у нас есть функция f(x) = x^2, то ее производная будет f'(x) = 2x. Это означает, что в каждой точке графика функции f(x) наклон прямой будет равен удвоенному значению аргумента.

Штрих используется в математике для решения различных задач, таких как определение максимумов и минимумов функций, нахождение касательной к графику функции в заданной точке и т.д.

Вопрос-ответ:

Зачем нужен штрих в математике?

Штрих в математике используется для обозначения производной функции по переменной. Он показывает, что мы берем производную функции и относим ее к переменной, по которой она берется.

Как правильно читать формулу с штрихом?

Формулу с штрихом читают как «экс дифференциал у экс» или «дифференциал у экс по экс». Это означает, что мы берем производную функции по переменной «х».

Как вычислить производную с помощью штриха?

Для вычисления производной с помощью штриха нужно взять функцию и поставить после нее штрих. Затем нужно дифференцировать функцию по указанной переменной. Например, если дана функция f(x) = x^2, то производная будет f'(x) = 2x.

Какие существуют правила дифференцирования с помощью штриха?

Существует несколько правил дифференцирования с помощью штриха. Например, правило дифференцирования произведения функций, правило дифференцирования сложной функции и т.д. Эти правила позволяют находить производные более сложных функций.

Можете привести примеры использования штриха в математике?

Конечно! Например, если дана функция f(x) = 3x^2, то производная будет f'(x) = 6x. Другой пример: если дана функция f(x) = sin(x), то производная будет f'(x) = cos(x).

Определение штриха и его свойства

Штрих в математике представляет собой символ, обозначающий производную функции по аргументу. Он используется для обозначения скорости изменения функции в заданной точке или её наклона касательной к графику функции в этой точке.

Штрих функции обозначается символом ‘‘. Например, если дана функция f(x), то её производная обозначается f'(x) или df(x)/dx.

Штрих обладает несколькими свойствами:

• Если функция f(x) дифференцируема в точке x, то её производная f'(x) существует в этой точке.
• Если функция f(x) имеет производную f'(x) в точке x, то она непрерывна в этой точке.
• Производная функции f(x) характеризует скорость изменения функции в данной точке. Если f'(x) > 0, то функция возрастает в этой точке, если f'(x) < 0, то функция убывает, и если f'(x) = 0, то функция имеет экстремум в этой точке.
• Для суммы двух функций f(x) и g(x) выполняется правило линейности производной: (f + g)'(x) = f'(x) + g'(x).
• Для произведения функции f(x) на константу a выполняется правило дифференцирования произведения: (a*f)'(x) = a*f'(x).
• Для произведения двух функций f(x) и g(x) выполняется правило дифференцирования произведения: (f*g)'(x) = f'(x)*g(x) + f(x)*g'(x).
• Для частного двух функций f(x) и g(x) выполняется правило дифференцирования частного: (f/g)'(x) = (f'(x)*g(x) — f(x)*g'(x))/g(x)^2.
• Для сложной функции f(g(x)) выполняется правило дифференцирования сложной функции: (f(g(x)))'(x) = f'(g(x))*g'(x).

Использование штриха в математике позволяет анализировать поведение функций и решать различные задачи, связанные с графиками и изменениями функций.

Примеры использования штриха в математике

Рассмотрим несколько примеров использования штриха:

ПримерФункцияПроизводная

1	f(x) = x^2	f'(x) = 2x
2	f(x) = sin(x)	f'(x) = cos(x)
3	f(x) = e^x	f'(x) = e^x
4	f(x) = ln(x)	f'(x) = 1/x

В первом примере, функция f(x) = x^2 имеет производную f'(x) = 2x. Это означает, что скорость изменения функции в каждой точке равна удвоенному значению аргумента x.

Во втором примере, функция f(x) = sin(x) имеет производную f'(x) = cos(x). Это означает, что скорость изменения функции в каждой точке равна значению косинуса аргумента x.

В третьем примере, функция f(x) = e^x имеет производную f'(x) = e^x. Это означает, что скорость изменения функции в каждой точке равна значению экспоненты с аргументом x.

В четвертом примере, функция f(x) = ln(x) имеет производную f'(x) = 1/x. Это означает, что скорость изменения функции в каждой точке обратно пропорциональна значению аргумента x.

Примеры использования штриха помогают нам лучше понять, как функции меняются в различных точках и облегчают решение задач, связанных с определением экстремумов и решением дифференциальных уравнений.

Значение штриха в производной

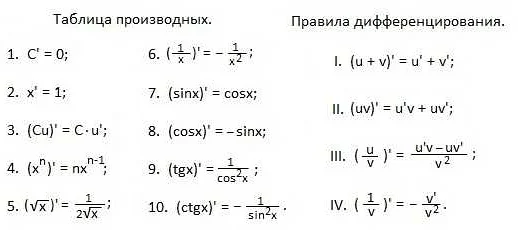
Штрих над функцией обозначает, что мы берем производную этой функции. Например, если у нас есть функция f(x), то ее производная будет обозначаться f'(x) или df(x)/dx. Символ штриха указывает на операцию взятия производной по переменной х.

Использование символа штриха облегчает запись и анализ математических выражений. Он позволяет четко указать, что именно мы хотим вычислить — производную функции по заданной переменной. Также штрих облегчает использование правил дифференцирования, так как с его помощью можно более легко записать производные сложных функций.

Примеры использования штриха в производной:

• Если у нас есть функция f(x) = x^2, то ее производная будет обозначаться f'(x) или df(x)/dx = 2x. Штрих указывает на то, что мы берем производную функции f(x) по переменной х.
• Если у нас есть функция g(t) = sin(t), то ее производная будет обозначаться g'(t) или dg(t)/dt = cos(t). Штрих здесь также указывает на операцию взятия производной по переменной t.

Понятие производной и ее связь с штрихом

Понятие производной связано с штрихом в том смысле, что производная функции в точке считается равной значению штриха функции в этой точке. Штрих функции обозначается обычно символом f'(x) или dy/dx. Штрих часто используется, чтобы обозначить первую производную функции.

Производная позволяет определить, как меняется функция в каждой точке ее области определения. Если значение производной положительно, то функция возрастает. Если значение производной отрицательно, то функция убывает. Значение производной равное нулю означает экстремум функции.

Примеры использования штриха и производной в математике включают вычисление скорости объекта, исследование оптимальных решений задач оптимизации и анализа графиков функций.

Как определить значение штриха в производной

Штрих в математике обозначает производную функции. Производная функции показывает, как быстро меняется значение функции при изменении ее аргумента. Значение штриха в производной можно определить с помощью различных методов.

Один из основных методов определения значения штриха в производной — использование первоначального определения производной. Согласно этому определению, производная функции в точке определяется пределом отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю.

Другим методом определения значения штриха в производной является использование правил дифференцирования. Существуют различные правила, позволяющие найти производную функции по известным производным более простых функций. Например, правило производной суммы гласит, что производная суммы двух функций равна сумме производных этих функций.

Также можно использовать таблицу производных, в которой перечислены известные производные основных функций. По этой таблице можно найти производную сложной функции, комбинируя известные производные.

Примеры использования этих методов можно найти в задачах на определение штриха в производной. Например, для функции f(x) = x^2 + 3x — 2 можно найти производную, используя правила дифференцирования или таблицу производных. Результатом будет функция f'(x) = 2x + 3.

Примеры использования штриха в производной

Штрих в производной используется для обозначения производной функции по переменной. Рассмотрим несколько примеров использования штриха.

ПримерФункцияПроизводная

1	f(x) = x^2	f'(x) = 2x
2	g(x) = sin(x)	g'(x) = cos(x)
3	h(x) = e^x	h'(x) = e^x

В первом примере функция f(x) = x^2 имеет производную f'(x) = 2x. Это означает, что скорость изменения функции в каждой точке равна удвоенному значению этой точки.

Во втором примере функция g(x) = sin(x) имеет производную g'(x) = cos(x). Это означает, что скорость изменения функции в каждой точке равна косинусу этой точки.

В третьем примере функция h(x) = e^x имеет производную h'(x) = e^x. Это означает, что скорость изменения функции в каждой точке равна экспоненте этой точки.

Штрих в производной является важным символом для обозначения производных функций и используется во многих математических выражениях.

Пример 1: Нахождение производной функции с помощью штриха

1. Для каждого слагаемого умножить его показатель степени на коэффициент. Таким образом, для слагаемого 2x^2 получаем 4x, для слагаемого 3x получаем 3.
2. Уменьшить показатель степени каждого слагаемого на 1. Для слагаемого 2x^2 получаем x, для слагаемого 3x получаем константу 0.

Теперь сложим полученные слагаемые: 4x + 3.

Таким образом, производная функции f(x) = 2x^2 + 3x — 5 равна f'(x) = 4x + 3.

Это значит, что график производной функции будет представлять собой прямую линию с наклоном 4 и смещением вверх на 3 единицы по оси y.

Функция f(x)Производная f'(x)

2x^2 + 3x — 5

4x + 3