Понятие и методы вычисления dy в математике. Как правильно найти значение?
Содержимое
- 1 Понятие и методы вычисления dy в математике. Как правильно найти значение?
- 1.1 dy в математике: определение и применение
- 1.2 dy как элементарное приращение
- 1.3 dy как дифференциал функции
- 1.4 dy как производная по y
- 1.5 dy как изменение функции по y
- 1.6 dy как приращение функции по y
- 1.7 dy в формулах и уравнениях
- 1.8 dy в геометрии и физике
- 1.9 Вопрос-ответ:
- 1.10 dy в прикладных задачах
- 1.11 Видео по теме:
Dy в математике — это производная функции y по переменной x. Узнайте, как найти dy и применить ее для решения задач и определения изменения функции.
В математике, dy — это дифференциал функции y по переменной x. Дифференциал является малым изменением или приращением функции. Он используется в дифференциальном исчислении для изучения изменения функций при изменении переменной.
Дифференциал dy обозначает, что мы рассматриваем изменение функции y в малом интервале изменения переменной x. Он указывает на то, как изменяется значение функции y при изменении переменной x на очень малое значение dx.
Значение dy можно найти с помощью процесса дифференцирования. Дифференцирование позволяет найти скорость изменения функции y по отношению к переменной x. Если у нас есть функция y(x), то дифференциал dy можно найти, вычислив производную функции y по переменной x.
dy = y'(x) * dx
Здесь y'(x) обозначает производную функции y по переменной x, а dx — очень малое значение, на которое мы изменяем переменную x.
Дифференциалы широко используются в математическом анализе, физике и других областях, где важно изучать изменение функций и их поведение при изменении переменных.
dy в математике: определение и применение
В математике символ «dy» обозначает дифференциал функции y от переменной x. Дифференциал представляет собой малое изменение функции при малом изменении переменной. Таким образом, «dy» показывает, как функция y меняется при изменении переменной x.
Дифференциалы широко используются в дифференциальном и интегральном исчислении. Они помогают найти производные функций и интегралы, а также решать различные задачи, связанные с изменением величин.
Как правило, дифференциалы записываются вместе с переменной, относительно которой производится дифференцирование. Например, если у нас есть функция y = f(x), то дифференциал этой функции будет записываться как dy = f'(x)dx, где f'(x) обозначает производную функции f(x) по переменной x.
Использование дифференциалов позволяет более точно аппроксимировать функции, а также анализировать их поведение. Они являются важным инструментом в математическом моделировании и решении задач из физики, экономики, биологии и других наук.
dy как элементарное приращение

В математике, dy представляет собой элементарное приращение или малое изменение функции y. Оно используется в дифференциальном исчислении для вычисления производной функции.
Когда мы говорим о приращении функции, мы рассматриваем, как функция меняется, когда аргумент изменяется на небольшое значение. В данном случае, dy показывает, как изменится значение функции y, когда аргумент меняется на малую величину dx.
Формально, dy определяется как произведение производной функции y по переменной x на малое изменение переменной dx. Математически записывается как:
dy = f'(x) * dx
Здесь f'(x) представляет производную функции y по переменной x.
Используя dy и dx, мы можем выразить дифференциал функции y как dy = f'(x) * dx. Это позволяет нам аппроксимировать изменение функции и вычислять ее производную в конкретной точке.
Таким образом, dy является ключевым понятием в дифференциальном исчислении и позволяет нам анализировать изменения функций и вычислять их производные.
dy как дифференциал функции
Дифференциал функции представляет собой приращение функции при бесконечно малом приращении независимой переменной. Обозначение dy часто используется в комбинации с обозначением dx, которое представляет собой бесконечно малое приращение независимой переменной.
Дифференциал функции можно выразить как произведение производной функции по независимой переменной на бесконечно малое приращение независимой переменной:
Дифференциал функцииОбозначение
| dy | = f'(x) * dx |
Здесь f'(x) обозначает производную функции f(x) по переменной x.
dy позволяет описать малое изменение значения функции при изменении независимой переменной. Оно играет важную роль в дифференциальном исчислении и используется при решении задач на определение экстремумов функций, построение касательных и нормалей к графику функции, а также в других областях математики и физики.
dy как производная по y
Для нахождения производной по переменной y необходимо использовать различные методы дифференцирования, такие как правило дифференцирования сложной функции, правило дифференцирования произведения, правило дифференцирования суммы и другие. Производная позволяет определить скорость изменения функции в зависимости от переменной y.
dy может использоваться для нахождения решений дифференциальных уравнений, а также в других областях математики и физики, где требуется анализ функций и их изменений.
dy как изменение функции по y
Дифференциал функции обозначается как dy и представляет собой малое приращение значения функции при изменении аргумента y. Формально, dy определяется как производная функции по переменной y, умноженная на малый приращение аргумента y.
dy = f'(y) * Δy
Здесь f'(y) обозначает производную функции f по переменной y, а Δy — малое приращение аргумента y.
Дифференциал dy позволяет описать, как изменяется значение функции при изменении аргумента y. Он является основным инструментом в дифференциальном исчислении и широко используется для нахождения производных и решения дифференциальных уравнений.
Использование дифференциала dy позволяет более точно описывать изменение функции по оси y и анализировать ее свойства. Он также упрощает процесс нахождения производных и решения различных математических задач.
dy как приращение функции по y
В математике символ dy обозначает приращение функции по переменной y. Он используется в дифференциальном исчислении для обозначения изменения значения функции при изменении переменной y.
Для вычисления приращения функции f(y) по переменной y используется следующая формула:
dy = f'(y) * Δy
где f'(y) — производная функции f(y) по переменной y, а Δy — изменение переменной y.
Таким образом, значение dy показывает, насколько изменится значение функции f(y), если переменная y изменится на значение Δy.
Использование символа dy позволяет удобно записывать производные функций и проводить дифференциальные операции.
dy в формулах и уравнениях
dy является производной функции y по переменной x, умноженной на дифференциал переменной x. Формально, dy может быть записано как:
dy = f'(x) * dx
где f'(x) — производная функции y по переменной x, dx — дифференциал переменной x.
dy можно использовать для нахождения приближенной величины изменения функции y при изменении аргументов. Это позволяет аппроксимировать функцию линейной функцией, что упрощает вычисления и анализ.
dy также используется для записи уравнений, относящихся к производным. Например, уравнение Эйлера:
dy/dx = f(x)
где f(x) — функция, описывающая зависимость y от x.
В общем случае, dy позволяет записывать и решать дифференциальные уравнения, которые играют важную роль в математике и физике.
dy в геометрии и физике
В геометрии dy может быть использовано для определения касательной к кривой в точке. Например, если у нас есть кривая, заданная уравнением y = f(x), то dy/dx будет производной этой функции. dy/dx показывает, как быстро изменяется y относительно x и может быть использовано для определения угла наклона касательной к кривой.
В физике dy может быть использовано для выражения изменения величины y в результате изменения других переменных. Например, если у нас есть функция y = f(x, t), где x и t — это переменные, dy будет показывать, как изменится y при изменении x и t. Это может быть полезно, когда мы исследуем зависимости между различными физическими величинами.
Таким образом, dy играет важную роль в геометрии и физике, помогая нам понять изменения и взаимосвязи между различными переменными и функциями.
Вопрос-ответ:
Что такое dy в математике?
dy в математике обозначает дифференциал функции y по переменной x. Он представляет собой бесконечно малое изменение функции y в результате бесконечно малого изменения переменной x. В более простых терминах, dy показывает, как изменится значение функции y, когда переменная x изменится на очень малую величину.
Как найти dy в математике?
Чтобы найти dy в математике, нужно взять производную функции y по переменной x и умножить полученное значение на дифференциал переменной x. Формально это записывается как dy = f'(x) * dx, где f'(x) — производная функции y по переменной x, а dx — дифференциал переменной x.
Как использовать dy в математических расчетах?
dy в математических расчетах используется для оценки изменения функции y при изменении переменной x. Он может быть полезен, например, при нахождении приближенных значений функции в окрестности заданной точки. Для этого необходимо умножить значение dy на некоторое малое изменение переменной x и добавить его к известному значению функции в точке x. Таким образом, можно получить приближенное значение функции в новой точке.
Как связаны dy и dx в математике?
dy и dx в математике связаны через производную функции y по переменной x. dy представляет собой произведение производной функции y по переменной x и дифференциала переменной x. Можно сказать, что dy и dx связаны как два бесконечно малых изменения переменных, одно из которых зависит от другого.
Можно ли считать dy и dx отдельными переменными в математике?
В математике dy и dx не являются отдельными переменными, а скорее обозначениями для бесконечно малых изменений функции y и переменной x соответственно. Они используются в процессе дифференцирования и имеют смысл только вместе с функцией, от которой они берутся.
dy в прикладных задачах

В прикладных задачах dy может быть использован для нахождения изменений величин, таких как скорость, ускорение, производная функции и т.д.
Дифференциал dy может быть выражен в виде дифференциала одной переменной или в виде дифференциала функции от нескольких переменных. Например, если у нас есть функция y = f(x), то dy может быть записано как dy = f'(x)dx, где f'(x) — производная функции f(x) по переменной x.
В прикладных задачах, dy может быть использован для аппроксимации изменения функции при небольших изменениях переменной или для расчета значений производной функции. Например, при решении задачи о движении тела, dy может представлять скорость тела, а dx — малое изменение времени. Таким образом, dy/dx будет представлять ускорение тела.
Использование dy в прикладных задачах позволяет аппроксимировать и анализировать изменения функций и их свойства в зависимости от изменения переменных. Это является важным инструментом в математическом моделировании и решении различных задач в физике, экономике, инженерии и других областях науки и техники.



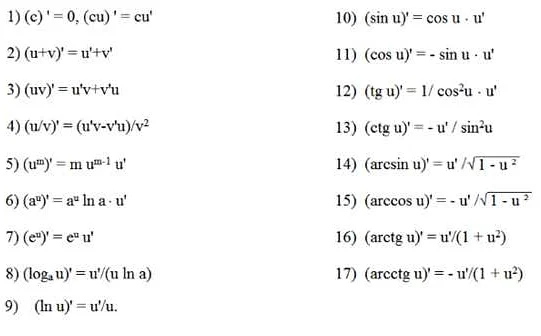
Dy в математике обозначает дифференциал функции y по переменной x. Это понятие приходится изучать при изучении дифференциального исчисления. Дифференциалы помогают найти приближенное значение изменения функции в окрестности точки. По сути, dy показывает, как изменится значение функции y при небольшом изменении значения x. Для нахождения dy нужно применить правило дифференцирования функции, которую нужно найти. Дифференцирование может быть сложным процессом, когда функция имеет сложный вид, но с помощью правил и методов дифференцирования можно найти точную формулу для вычисления dy. Таким образом, dy позволяет анализировать поведение функции и строить графики, что важно во многих областях науки и техники.
Статья очень понятно объясняет, что такое «dy» в математике и как его найти. Я очень благодарна автору за доступный и простой язык, который позволяет даже не очень математически грамотным людям понять этот термин. Теперь я знаю, что «dy» обозначает дифференциал и используется при нахождении производной функции. Алгоритм, который автор предлагает для нахождения «dy», ясен и понятен. Я сразу попробовала его применить на своем уравнении и получила правильный результат! Теперь мне гораздо проще справляться с задачами, связанными с производными. Большое спасибо за полезную статью!
Я всегда интересовалась математикой, но термин «dy» всегда вызывал у меня некоторую путаницу. К счастью, я наконец-то разобралась! Выражение «dy» является дифференциалом функции y относительно переменной x. Оно помогает нам узнать, как изменяется значение y при изменении x. Важно понимать, что «dy» не является отдельной переменной, а всего лишь обозначением для дифференциала. Теперь, как найти «dy»? Для этого нужно взять производную функции y по переменной x и умножить ее на изменение переменной x. Можно представить это как мгновенное изменение функции y при изменении x. Таким образом, «dy» позволяет нам оценить изменение y в окрестности выбранной точки на графике. Для меня это понимание «dy» является важным шагом в понимании математических концепций. Теперь я могу использовать «dy» для решения более сложных задач и лучше взаимодействовать с математическими моделями.
Честно говоря, всегда была немного запутана, когда встречала в математике такие обозначения, как «dy». Кажется, что они имеют какой-то особый смысл и я не знаю, как их интерпретировать. Но недавно я решила разобраться в этом вопросе и оказалось, что все гораздо проще, чем я думала. «dy» — это дифференциал функции y. Он указывает на то, что мы рассматриваем очень маленькое изменение функции y в окрестности какой-то точки. На самом деле, «dy» — это просто другая запись для производной функции y по переменной x. Как найти «dy»? Для этого нужно использовать дифференциальное исчисление. Если у нас есть функция y(x), то производная этой функции dy/dx показывает, как изменяется y при изменении x. Производная можно рассчитать при помощи правил дифференцирования, которые есть в математическом анализе. Таким образом, «dy» — это просто другая форма записи для производной функции. Зная «dy», мы можем анализировать, как функция меняется в конкретной точке и как эту зависимость можно использовать для решения различных задач. Надеюсь, это разъяснение помогло вам как и мне, и теперь «dy» уже не кажется таким загадочным и непонятным обозначением.