Что значит функция в математике

Функция в математике — это отображение одного множества (области определения) в другое множество (область значений), где каждому элементу из области определения соответствует ровно один элемент из области значений. Функции широко используются в математическом анализе, алгебре и других областях математики для описания зависимостей между величинами и решения различных задач.

Функция — одно из ключевых понятий в математике, которое широко применяется во многих разделах науки. Она позволяет описать зависимость одной величины от другой и является основой для многих математических моделей и теорий. Функция представляет собой правило, с помощью которого каждому элементу множества, называемого областью определения, ставится в соответствие элемент другого множества, называемого областью значений.

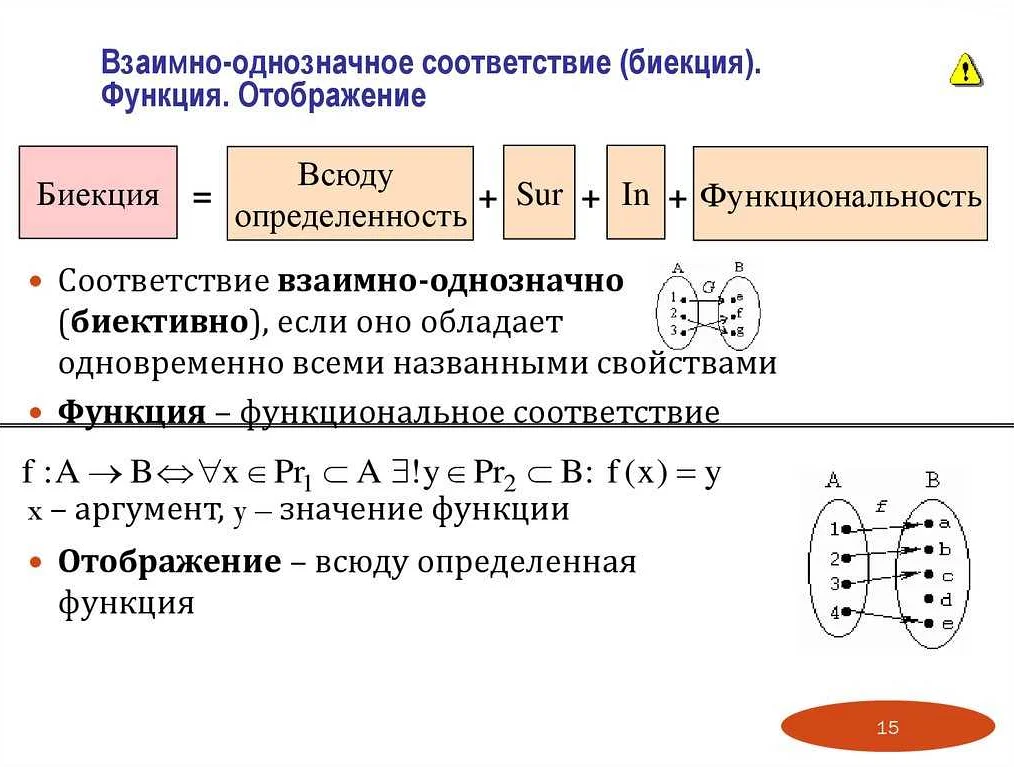
Функция в математике обычно обозначается символом f и записывается в виде f(x), где x — элемент области определения. Значение функции для каждого элемента области определения может быть определено однозначно или многозначно, в зависимости от конкретной функции. Однозначная функция называется инъективной, многозначная — сюръективной, а если она инъективна и сюръективна одновременно, то она называется биективной.

Примером функции может служить функция f(x) = 2x, где x — любое число. В этом случае значение функции равно удвоенному значению x. Например, если x = 3, то f(x) = 2 * 3 = 6. Если x = -5, то f(x) = 2 * (-5) = -10. И так далее. Таким образом, функция f(x) = 2x устанавливает соответствие между каждым числом x и его удвоенным значением.

Функции имеют важное значение в различных областях науки и техники. Они позволяют описывать и анализировать различные явления, моделировать процессы и решать задачи. Кроме того, функции являются основой для изучения других математических понятий, таких как производная, интеграл, дифференциальное уравнение и многое другое. Поэтому понимание функций и их свойств является важной составляющей математической грамотности и необходимо для успешного обучения и работы во многих областях науки и техники.

Определение функции в математике

Функция обозначается символом f и записывается как f(x), где x — элемент из области определения. Значение функции в точке x обозначается как f(x) и соответствует элементу из области значений.

Примеры функций в математике:

• Линейная функция: f(x) = mx + b, где m и b — константы.
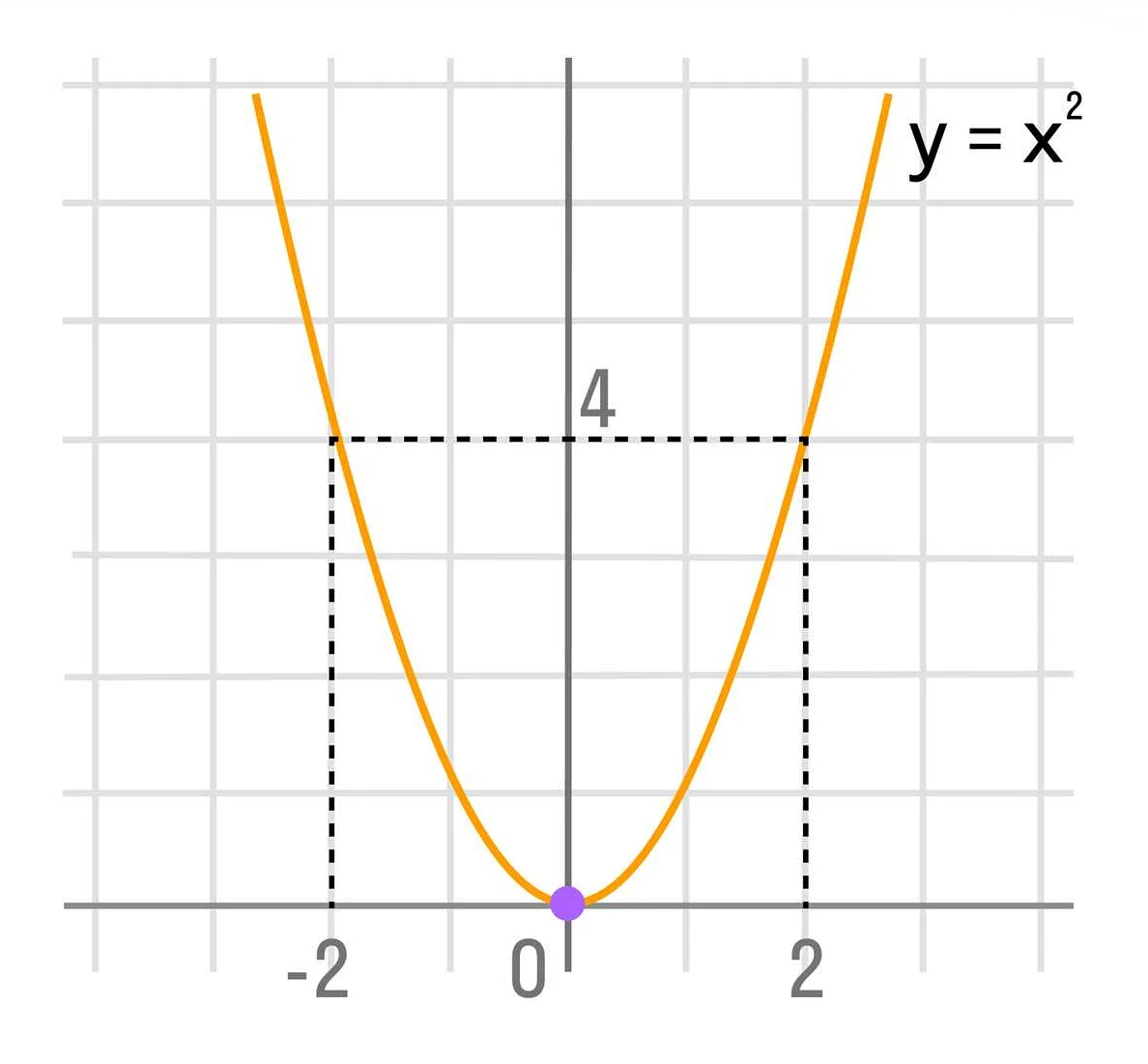
• Квадратная функция: f(x) = ax^2 + bx + c, где a, b и c — константы.
• Синусоидальная функция: f(x) = A * sin(B * x + C), где A, B и C — константы.

Видео по теме:

Примеры функций

Вот некоторые примеры функций:

1. Линейная функция: y = 2x + 3. В этом примере, значение y зависит от значения x в соответствии с формулой y равной двум умноженному на x, плюс три.

2. Квадратичная функция: y = x^2 + 5x + 6. Здесь, значение y зависит от значения x в соответствии с формулой y равной x в квадрате, плюс пять умноженное на x, плюс шесть.

3. Тригонометрическая функция: y = sin(x). В данном случае, значение y зависит от значения x с помошью синуса угла x.

4. Экспоненциальная функция: y = 2^x. Здесь, значение y зависит от значения x в соответствии с формулой y равной двум в степени x.

5. Логарифмическая функция: y = log(x). В этом примере, значение y зависит от значения x через логарифм x.

Это лишь некоторые примеры функций, которые широко используются в математике и ежедневной жизни.

Связь между аргументами и значениями функции

Связь между аргументами и значениями функции можно представить в виде таблицы, где в первом столбце указываются значения аргументов, а во втором столбце — соответствующие им значения функции. Такая таблица называется «таблицей значений функции».

АргументыЗначения функции

x	f(x)
1	3
2	5
3	7

Например, рассмотрим функцию f(x) = 2x + 1. Если подставить значения аргументов x = 1, x = 2 и x = 3 в эту функцию, то получим соответствующие значения функции: f(1) = 3, f(2) = 5 и f(3) = 7. Таким образом, связь между аргументами и значениями функции f(x) = 2x + 1 можно представить в виде следующей таблицы:

xf(x)

1	3
2	5
3	7

Вопрос-ответ:

Как можно определить функцию в математике?

Функция в математике — это отношение между двумя множествами, где каждому элементу первого множества соответствует ровно один элемент второго множества.

Какие примеры функций можно привести?

Примеры функций в математике могут быть разнообразными. Например, функция, которая возвращает квадрат числа: f(x) = x^2. Или функция, которая возвращает синус угла: f(x) = sin(x).

Какие свойства имеют функции в математике?

Функции в математике обладают рядом свойств. Например, каждому элементу исходного множества соответствует ровно один элемент области значений. Кроме того, функции могут быть однозначными (инъективными), когда каждому элементу области определения соответствует ровно один элемент области значений, или могут быть многозначными. Также функции могут быть строго возрастающими или строго убывающими.

Какие математические операции можно выполнять с функциями?

С функциями можно выполнять различные операции, такие как сложение и вычитание, умножение и деление, композиция функций. Например, можно сложить две функции: f(x) + g(x). Или можно вычислить произведение двух функций: f(x) * g(x).

Какие области применения имеют функции в математике?

Функции в математике имеют широкие области применения. Они используются в алгебре, геометрии, анализе, статистике и других разделах математики. Функции также находят применение в физике, экономике, компьютерных науках и других научных и прикладных областях.

Как определяется функция в математике?

Функция в математике — это отношение между двумя множествами, где каждому элементу первого множества сопоставлен единственный элемент второго множества. Функция описывает зависимость между входными и выходными значениями, где каждому входному значению соответствует ровно одно выходное значение.

Какие бывают примеры функций в математике?

В математике существует множество примеров функций. Например, функция f(x) = 2x описывает удвоение входного значения. Если мы введем x = 3, то получим f(3) = 6. Другой пример функции — f(x) = x^2, которая описывает возведение входного значения в квадрат. Если мы введем x = 4, то получим f(4) = 16.

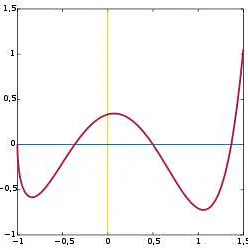
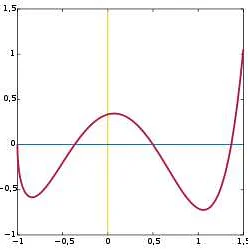
График функции и его свойства

График функции обычно представляется на плоскости с осями координат. Горизонтальная ось называется осью абсцисс, вертикальная ось — осью ординат. Каждая точка на графике функции соответствует значению аргумента и значению функции в этой точке.

Свойства графика функции:

• График функции может быть непрерывным или разрывным. Непрерывный график не имеет линий, разрывный график имеет разрывы.
• График функции может иметь точки экстремума — максимумы и минимумы. Максимум — это точка, в которой функция принимает наибольшее значение, минимум — точка, в которой функция принимает наименьшее значение.
• График функции может иметь точки перегиба — точки, в которых меняется направление выпуклости или вогнутости графика.
• График функции может иметь асимптоты — линии, которыми график функции стремится к бесконечности или приближается к определенным значениям.

Изучение графика функции позволяет анализировать ее свойства, находить экстремумы, определять области возрастания и убывания функции, а также находить значения функции при заданных значениях аргумента.

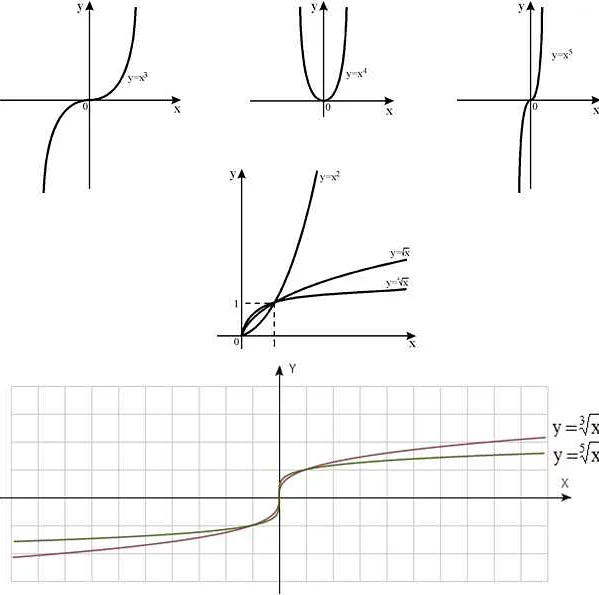
Виды функций в математике

В математике существует множество различных видов функций, каждая из которых обладает своими особенностями и свойствами. Некоторые из наиболее распространенных видов функций включают:

1. Линейная функция — это функция, которая описывается уравнением вида y = kx + b, где k и b — константы. Графиком линейной функции является прямая линия.
2. Квадратичная функция — это функция, которая описывается уравнением вида y = ax^2 + bx + c, где a, b и c — константы. Графиком квадратичной функции является парабола.
3. Степенная функция — это функция, которая описывается уравнением вида y = ax^n, где a и n — константы. Графиком степенной функции может быть прямая линия или кривая.
4. Тригонометрическая функция — это функция, которая использует тригонометрические операции, такие как синус, косинус, тангенс и их обратные функции. Некоторые примеры тригонометрических функций включают синусную функцию (y = sin(x)) и косинусную функцию (y = cos(x)). Графики тригонометрических функций имеют периодический характер.
5. Экспоненциальная функция — это функция, которая описывается уравнением вида y = a^x, где a — константа. График экспоненциальной функции имеет быстрое возрастание или убывание.
6. Логарифмическая функция — это функция, которая является обратной к экспоненциальной функции. Она описывается уравнением вида y = log_a(x), где a — константа. График логарифмической функции имеет быстрое возрастание или убывание.

Это лишь некоторые из основных видов функций, которые используются в математике. Каждый вид функции имеет свои уникальные свойства и применения, и их изучение является важной составляющей математического анализа и алгебры.

Как определить, является ли график функции прямой

Если уравнение функции имеет другой вид, то для определения, является ли ее график прямой, необходимо построить этот график и проанализировать его свойства. Прямая функция характеризуется тем, что все ее точки лежат на одной прямой линии. Если график функции имеет прямолинейный вид без изгибов и перегибов, то он является прямой.

Важно отметить, что график функции может быть прямой только в определенном интервале значений аргумента x. Например, функция y = 2x + 1 будет иметь прямой график на всей числовой прямой, а функция y = x^2 будет иметь прямой график только на отрезке [-∞, 0].

Операции с функциями

В математике функции могут быть объединены с помощью различных операций, которые позволяют строить новые функции на основе уже существующих. Вот некоторые из основных операций с функциями:

1. Сложение функций: Если имеется две функции f(x) и g(x), то их сумма f(x) + g(x) представляет собой новую функцию, значения которой равны сумме значений f(x) и g(x) в каждой точке x.

2. Вычитание функций: Если имеется две функции f(x) и g(x), то их разность f(x) — g(x) представляет собой новую функцию, значения которой равны разности значений f(x) и g(x) в каждой точке x.

3. Умножение функций: Если имеется две функции f(x) и g(x), то их произведение f(x) * g(x) представляет собой новую функцию, значения которой равны произведению значений f(x) и g(x) в каждой точке x.

4. Деление функций: Если имеется две функции f(x) и g(x), то их частное f(x) / g(x) представляет собой новую функцию, значения которой равны частному значений f(x) и g(x) в каждой точке x. При этом g(x) не должна быть равна нулю, так как деление на ноль не определено.

5. Композиция функций: Композиция функций f(g(x)) представляет собой новую функцию, которая получается подстановкой функции g(x) вместо переменной x в функции f(x). То есть, сначала вычисляются значения функции g(x), а затем эти значения подставляются в функцию f(x).

Операции с функциями широко используются в математике и ее приложениях. Они позволяют создавать более сложные функции на основе простых и анализировать их свойства.

Значение функции в различных точках

Значение функции в математике определяется по её аргументу, т.е. входному значению. При подстановке различных значений аргумента в функцию получаем соответствующие значения функции.

Например, рассмотрим функцию f(x) = 2x + 3. Если подставить различные значения для x, мы получим соответствующие значения функции:

• При x = 0, значение функции будет f(0) = 2(0) + 3 = 3.
• При x = 1, значение функции будет f(1) = 2(1) + 3 = 5.
• При x = -2, значение функции будет f(-2) = 2(-2) + 3 = -1.

Таким образом, значение функции может изменяться в зависимости от значения аргумента. Зная функцию и подставляя различные значения аргумента, мы можем определить соответствующие значения функции в различных точках.