Что такое неопределенный интеграл в математике

Неопределенный интеграл – это основной инструмент в математическом анализе, позволяющий находить примитивную функцию для заданной производной. В данной статье рассмотрены основы неопределенного интеграла и его связь с определенным интегралом. Описаны основные методы решения неопределенных интегралов и представлены примеры их использования. Подробные объяснения и простые примеры помогут понять сущность неопределенного интеграла и его применение в математике.

Неопределенный интеграл — это одна из основных концепций математического анализа, которая позволяет находить функцию, производная которой является заданной функцией. Он является обратной операцией к дифференцированию и широко применяется в различных областях, включая физику, экономику и инженерию.

Неопределенный интеграл обозначается символом ∫ и имеет вид ∫f(x)dx, где f(x) — это интегрируемая функция, а dx — элементарный приращение аргумента. Неопределенный интеграл позволяет найти бесконечное множество функций, производной которых является заданная функция f(x).

Вычисление неопределенного интеграла происходит с помощью методов интегрирования, таких как метод замены переменной, метод интегрирования по частям и метод дробно-рациональных функций. Каждый из этих методов имеет свои специфические правила и приемы, которые используются для нахождения интегралов различных видов функций.

Неопределенный интеграл имеет много практических применений. Например, он может использоваться для нахождения площади под кривой, вычисления работы и энергии в физике, а также для решения задач оптимизации и моделирования в экономике и инженерии. Понимание неопределенного интеграла и его вычисление является важным навыком для студентов и профессионалов в различных областях науки и техники.

Неопределенный интеграл в математике

Функция F(x) называется антипроизводной функции f(x) на интервале [a, b], если для любого x из этого интервала верно равенство F'(x) = f(x), где F'(x) обозначает производную функции F(x).

Неопределенный интеграл от функции f(x) обозначается символом ∫f(x)dx и вычисляется путем нахождения антипроизводной функции F(x) с добавлением произвольной постоянной C:

∫f(x)dx = F(x) + C

Здесь C — постоянная интегрирования, которая может принимать любое действительное значение.

Неопределенный интеграл позволяет находить площадь под кривой, а также решать множество задач, связанных с нахождением функций, производные которых уже известны.

Для вычисления неопределенного интеграла используются различные методы, такие как метод замены переменной, метод интегрирования по частям и другие.

Определение и смысл

Неопределенный интеграл обозначается символом ∫ (интеграл) и записывается в виде ∫f(x)dx, где f(x) — подынтегральная функция, а dx — дифференциал переменной интегрирования.

Смысл неопределенного интеграла заключается в нахождении площади под кривой графика функции f(x) на определенном интервале. Кривая представляет собой график функции, а площадь под ней равна значению неопределенного интеграла.

Вычисление неопределенного интеграла осуществляется с использованием различных методов, таких как замена переменной, интегрирование по частям и другие. Каждый метод имеет свои особенности и применяется в зависимости от сложности функции и условий задачи.

Основные свойства неопределенного интеграла

1. Линейность:

Неопределенный интеграл обладает свойством линейности. Это означает, что для любых двух функций f(x) и g(x), и чисел a и b, выполняется следующее равенство:

∫(af(x) + bg(x))dx = a∫f(x)dx + b∫g(x)dx

2. Интегрирование производной:

Если функция f(x) является производной другой функции F(x), то неопределенный интеграл от f(x) будет равен функции F(x) с добавлением произвольной постоянной C:

∫f(x)dx = F(x) + C

3. Замена переменной:

Неопределенный интеграл можно вычислить с помощью замены переменной. Если имеется функция f(u) и функция g(x) такая, что u = g(x), то неопределенный интеграл от f(g(x)) будет равен неопределенному интегралу от f(u) с заменой переменной u = g(x) и умножением на производную функции g(x):

∫f(g(x))g'(x)dx = ∫f(u)du

4. Интегрирование по частям:

Если имеются две функции f(x) и g(x), то неопределенный интеграл от произведения этих функций можно найти с помощью формулы интегрирования по частям:

∫f(x)g'(x)dx = f(x)g(x) — ∫g(x)f'(x)dx

5. Интегрирование рациональных функций:

Рациональная функция представляется как отношение двух многочленов, и ее неопределенный интеграл может быть найден с помощью метода частных дробей или других специальных методов вычисления интегралов.

Эти основные свойства неопределенного интеграла позволяют вычислять интегралы различных функций и использовать интегралы в решении математических задач.

Методы вычисления неопределенного интеграла

Одним из основных методов вычисления неопределенного интеграла является метод интегрирования по частям. Он основан на формуле интегрирования по частям:

\( \int u(x) v'(x) \,dx = u(x) v(x) — \int v(x) u'(x) \,dx \)

где \( u(x) \) и \( v(x) \) — две функции, а \( u'(x) \) и \( v'(x) \) — их производные.

Другим методом вычисления неопределенного интеграла является метод замены переменной. Он заключается в замене переменной в интеграле с целью упрощения выражения. Обычно используются замены, которые приводят к интегралам от более простых функций, например, тригонометрических или логарифмических.

Также существуют специальные методы для вычисления интегралов от различных классов функций, например, метод тригонометрических подстановок или метод дробно-рациональных подстановок.

Некоторые интегралы можно вычислить с помощью таблицы интегралов, в которой представлены значения интегралов от базовых функций. Это позволяет сразу найти аналитическое выражение для интеграла.

В ряде случаев, когда аналитическое выражение для интеграла не может быть найдено, используют численные методы вычисления интеграла, например, метод прямоугольников, метод тrapezoid или метод Симпсона.

Выбор метода вычисления неопределенного интеграла зависит от конкретной функции и ее свойств. Иногда может потребоваться использование нескольких методов для получения аналитического выражения для интеграла.

Таблица основных неопределенных интегралов

Таблица основных неопределенных интегралов содержит список известных неопределенных интегралов и их соответствующих формул. При решении задач, связанных с вычислением неопределенного интеграла, таблица может быть полезным инструментом, позволяющим быстро находить ответы.

Вот некоторые из основных неопределенных интегралов, которые присутствуют в таблице:

ФункцияНеопределенный интеграл

1	∫ 1 dx = x + C
x^n	∫ x^n dx = (x^(n+1))/(n+1) + C
e^x	∫ e^x dx = e^x + C
sin(x)	∫ sin(x) dx = -cos(x) + C
cos(x)	∫ cos(x) dx = sin(x) + C
1/x	∫ 1/x dx = ln|x| + C

Это лишь некоторые примеры функций, которые можно найти в таблице. Однако, следует отметить, что не все неопределенные интегралы можно выразить в явном виде. В таких случаях можно использовать численные методы или другие техники для приближенного нахождения значения интеграла.

Таблица основных неопределенных интегралов может быть полезным инструментом при решении задач, связанных с вычислением интегралов. Однако, важно помнить, что использование таблицы требует понимания принципов и правил интегрирования, чтобы правильно применять формулы из таблицы.

Приложение неопределенного интеграла: площадь под кривой

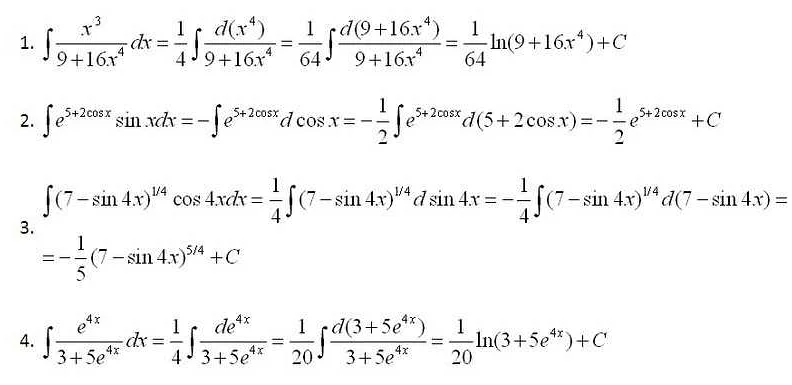
Неопределенный интеграл в математике позволяет вычислить площадь под кривой на заданном интервале. Это важное приложение интеграла, которое находит применение в различных областях, включая физику, экономику и инженерные науки.

Чтобы вычислить площадь под кривой, нужно сначала найти антипроизводную функции, которая задает кривую. Затем неопределенный интеграл от функции на заданном интервале даст нам площадь под кривой на этом интервале.

Для вычисления неопределенного интеграла можно использовать различные методы, такие как метод замены переменной или метод интегрирования по частям. Выбор метода зависит от сложности функции и доступных интегральных формул.

При вычислении площади под кривой важно учитывать границы интервала и правильно определить пределы интегрирования. Это позволяет получить точный результат и учесть площадь только под нужной частью кривой.

Приложение неопределенного интеграла: площадь под кривой находит свое применение в различных задачах. Например, в физике можно использовать этот метод для вычисления площади под графиком скорости от времени и получения пути, пройденного телом. В экономике и финансовой математике можно вычислить площадь под графиком спроса и получить общую сумму товаров или услуг.

Важно отметить, что вычисление площади под кривой с помощью неопределенного интеграла является приближенным методом. Более точные результаты можно получить с помощью определенного интеграла, который позволяет вычислить площадь более точно и учесть все значения функции на заданном интервале.

Связь неопределенного интеграла с производной

Если функция \(f(x)\) является непрерывной на отрезке \([a, b]\), то ее неопределенный интеграл \(\int f(x) dx\) существует и может быть вычислен. В этом случае производная функции \(F(x)\), равная интегралу от функции \(f(x)\), будет равна исходной функции: \(F'(x) = f(x)\). То есть, производная функции является первообразной функции.

Обратно, если функция \(F(x)\) является непрерывной на интервале \((a, b)\) и ее производная существует на этом интервале, то неопределенный интеграл от производной функции будет равен исходной функции с добавлением постоянной: \(\int F'(x) dx = F(x) + C\), где \(C\) — произвольная постоянная.

Таким образом, неопределенный интеграл и производная представляют собой взаимно обратные операции. Если взять производную от неопределенного интеграла функции, то получится исходная функция, а если взять неопределенный интеграл от производной функции, то получится исходная функция с добавлением постоянной.

Примеры вычисления неопределенного интеграла

Рассмотрим несколько примеров вычисления неопределенного интеграла:

1. Вычисление интеграла ∫(3x^2 + 2x + 1)dx:

Сначала найдем интеграл каждого слагаемого по отдельности:

∫3x^2dx = x^3 + C1

∫2xdx = x^2 + C2

∫1dx = x + C3

Суммируем полученные интегралы:

∫(3x^2 + 2x + 1)dx = x^3 + x^2 + x + C

где C = C1 + C2 + C3 – произвольная постоянная.

2. Вычисление интеграла ∫(2sinx + 3cosx)dx:

∫2sinxdx = -2cosx + C1

∫3cosxdx = 3sinx + C2

Суммируем полученные интегралы:

∫(2sinx + 3cosx)dx = -2cosx + 3sinx + C

где C = C1 + C2 – произвольная постоянная.

3. Вычисление интеграла ∫(1/x)dx:

∫(1/x)dx = ln|x| + C

где ln|x| – натуральный логарифм абсолютного значения x, C – произвольная постоянная.

Таким образом, вычисление неопределенного интеграла позволяет найти функцию, производной которой является заданная функция. Это важный инструмент в математике и находит применение в различных областях, таких как физика, экономика, и т.д.

Важность неопределенного интеграла в математике и её применения

Неопределенный интеграл обладает следующими важными свойствами:

1. Линейность	Неопределенный интеграл обладает свойством линейности, что позволяет легко находить интегралы от сумм и разностей функций.
2. Интегрирование по частям	Интегрирование по частям позволяет связать интеграл от произведения двух функций с интегралом от одной из них.
3. Замена переменной	Замена переменной позволяет связать интеграл от функции с интегралом от другой функции, что может значительно упростить вычисления.

Неопределенный интеграл имеет множество применений в различных областях науки и техники:

• Физика. Неопределенный интеграл используется для нахождения площадей, объемов и центров тяжести различных фигур.
• Экономика. Интегралы применяются для определения экономических показателей, таких как общая прибыль и общий спрос.
• Инженерия. Интегралы используются при решении задач, связанных с расчетами в машиностроении, электротехнике и других отраслях.
• Криптография. Интегралы применяются для разработки алгоритмов шифрования и дешифрования информации.

Таким образом, неопределенный интеграл является мощным математическим инструментом, который находит применение во многих областях науки и техники. Он позволяет решать сложные задачи и получать аналитические выражения для различных функций.

Вопрос-ответ:

Какое определение имеет неопределенный интеграл в математике?

Неопределенный интеграл — это обратный процесс к дифференцированию. Он позволяет найти функцию, производная которой равна заданной функции.

Как вычислять неопределенный интеграл?

Для вычисления неопределенного интеграла необходимо использовать методы интегрирования. Одним из основных методов является метод замены переменной, а также методы интегрирования по частям и интегрирования дробно-рациональных функций.

Какой смысл имеет константа при вычислении неопределенного интеграла?

При вычислении неопределенного интеграла в результате мы получаем функцию, которая отличается от исходной функции лишь на константу. Это происходит потому, что производная постоянной равна нулю.

Какие есть особенности при вычислении неопределенного интеграла?

При вычислении неопределенного интеграла необходимо учитывать, что интеграл от суммы или разности двух функций равен сумме или разности интегралов этих функций. Кроме того, интеграл от произведения функций может быть вычислен с использованием метода интегрирования по частям.

Видео по теме: