Что такое определенный интеграл в математике
Содержимое
- 1 Что такое определенный интеграл в математике
- 1.1 Определенный интеграл в математике: понятие и основные принципы
- 1.2 Основные понятия определенного интеграла
- 1.3 Связь с неопределенным интегралом
- 1.4 Функции Римана и разбиения отрезка
- 1.5 Пределы Римана и сумма Римана
- 1.6 Интегрируемость функции на отрезке
- 1.7 Основные свойства определенного интеграла
- 1.8 Примеры вычисления определенного интеграла
- 1.9 Практическое применение определенного интеграла
- 1.10 Видео по теме:
Определенный интеграл в математике – это инструмент для вычисления площади под графиком функции на заданном интервале. Узнайте, как работает определенный интеграл и как его использовать для решения задач.
Определенный интеграл является одним из основных понятий математического анализа. Эта математическая операция позволяет найти площадь под кривой на заданном отрезке, а также решать разнообразные задачи, связанные с нахождением средних значений функций.
Основной идеей определенного интеграла является разбиение заданного отрезка на бесконечно малые части и нахождение суммы площадей этих частей. Для этого используется так называемая интегральная сумма, которая представляет собой сумму значений функции, умноженных на ширину соответствующего интервала разбиения.
Определенный интеграл обозначается символом ∫ и имеет вид ∫[a, b] f(x) dx, где a и b — границы отрезка, f(x) — интегрируемая функция. Результатом вычисления определенного интеграла является число, которое называется значением интеграла и обозначается как I. Значение интеграла показывает площадь фигуры, ограниченной графиком функции f(x), осью абсцисс и вертикальными прямыми x = a и x = b.
Например, чтобы найти площадь под кривой графика функции f(x) = x^2 на отрезке [0, 2], мы можем использовать определенный интеграл. Вычисление интеграла будет состоять из таких шагов: разбить отрезок [0, 2] на небольшие интервалы, найти площадь каждого интервала, сложить полученные значения и получить итоговую площадь. В данном случае, результатом вычисления интеграла будет число 8/3, что является площадью фигуры, ограниченной графиком функции f(x) = x^2, осью абсцисс и прямыми x = 0 и x = 2.
Определенный интеграл в математике: понятие и основные принципы
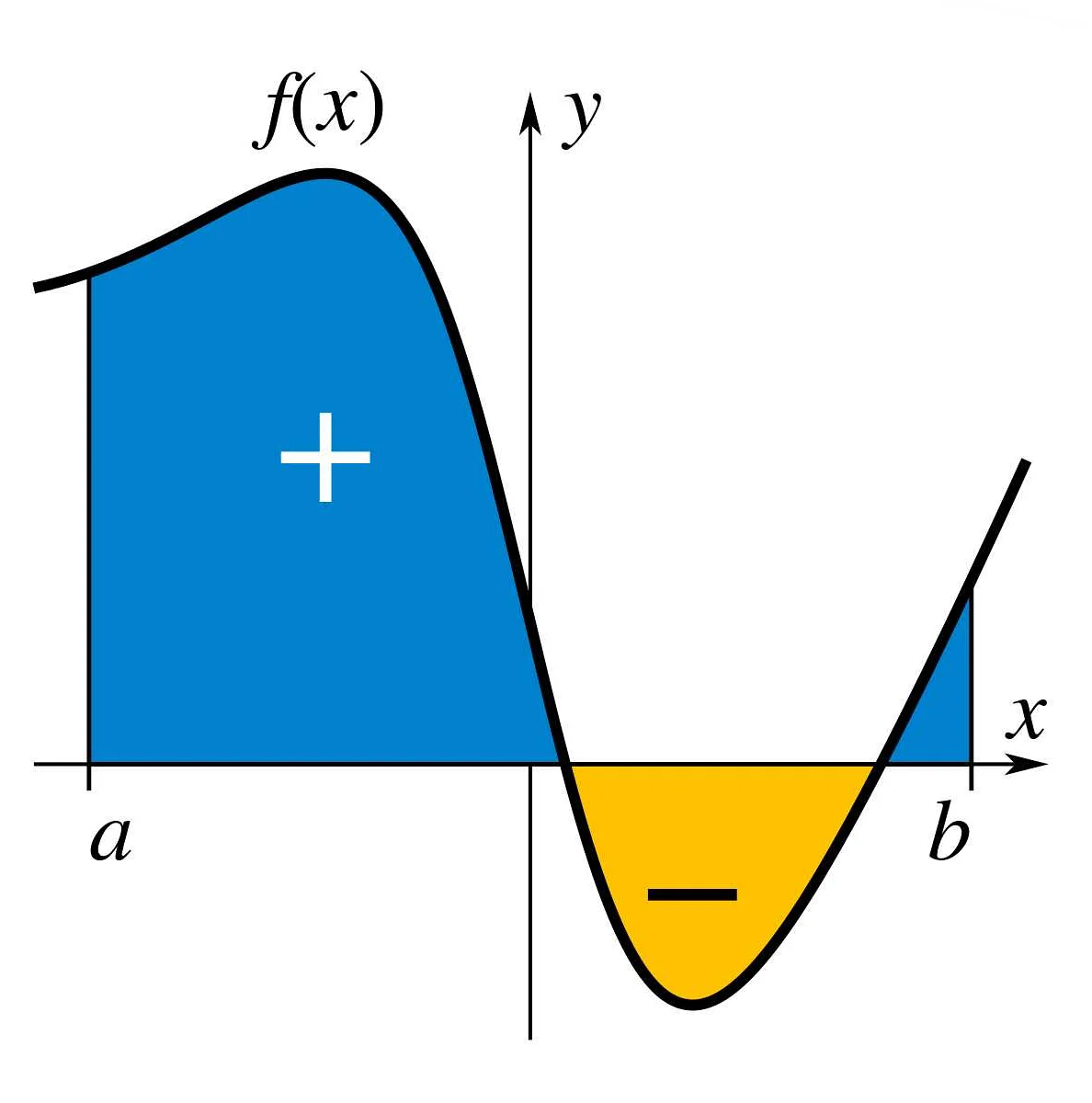
Определенный интеграл обозначается символом ∫ и имеет следующий вид:
∫[a, b] f(x) dx,
где f(x) — интегрируемая функция, a и b — границы интегрирования, dx — бесконечно малый интервал по оси абсцисс.
Определенный интеграл можно рассматривать как предел суммы площадей бесконечного числа прямоугольников, на которые разбивается фигура под графиком функции.
Для вычисления определенного интеграла существует несколько методов, включая методы прямоугольников, трапеций и Симпсона. Однако, основной принцип вычисления состоит в разбиении интервала интегрирования на маленькие отрезки и приближении площади под графиком функции суммой площадей этих отрезков.
Важным свойством определенного интеграла является его независимость от выбора антипроизводной функции. Это означает, что значение определенного интеграла не зависит от того, какую антипроизводную функции мы выберем.
Определенный интеграл находит широкое применение в различных областях науки и техники, включая физику, экономику, статистику и теорию вероятностей. Он позволяет решать разнообразные задачи, связанные с вычислением площадей, объемов, средних значений и многих других величин.
Основные понятия определенного интеграла
Определенный интеграл функции $f(x)$ на отрезке $[a, b]$ обозначается следующим образом:
$$\int_a^b f(x) \, dx$$
Основная идея определенного интеграла состоит в разбиении отрезка $[a, b]$ на бесконечное количество малых отрезков и вычислении суммы площадей прямоугольников, ограниченных функцией $f(x)$ и осью $x$. При этом ширина каждого прямоугольника стремится к нулю, а высота равна значению функции в соответствующей точке.
Определенный интеграл можно вычислить с помощью интегральной суммы:
$$\int_a^b f(x) \, dx = \lim_{{n \to \infty}} \sum_{{i=1}}^n f(x_i) \Delta x_i$$
где $n$ — количество подынтервалов, на которые разбит отрезок $[a, b]$, $x_i$ — произвольная точка на $i$-ом подынтервале, $\Delta x_i$ — ширина $i$-го подынтервала.
Определенный интеграл имеет следующие основные свойства:
СвойствоФормула
| Линейность | $\int_a^b (f(x) + g(x)) \, dx = \int_a^b f(x) \, dx + \int_a^b g(x) \, dx$ |
| Аддитивность | $\int_a^b f(x) \, dx + \int_b^c f(x) \, dx = \int_a^c f(x) \, dx$ |
| Интеграл от постоянной | $\int_a^b k \, dx = k(b — a)$ |
| Интеграл от монотонной функции | $\int_a^b f(x) \, dx = -\int_b^a f(x) \, dx$, если $f(x)$ монотонна на $[a, b]$ |
| Интеграл от симметричной функции | $\int_{-a}^a f(x) \, dx = 0$, если $f(x)$ симметрична относительно оси $x$ |
Определенный интеграл позволяет решать различные задачи, такие как нахождение площади под кривой, вычисление среднего значения функции, определение массы объекта с переменной плотностью и другие. Он также является одним из основных инструментов в математическом моделировании и физике.
Связь с неопределенным интегралом
Неопределенный интеграл позволяет найти функцию, производная которой равна данной функции. Он представляет собой семейство функций, отличающихся друг от друга на константу. Символ, обозначающий неопределенный интеграл, называется интегральной константой.
Определенный интеграл, в свою очередь, позволяет найти площадь, ограниченную кривой и осями координат на заданном интервале. Определенный интеграл является числовым значением и не содержит интегральной константы.
Связь между определенным и неопределенным интегралом заключается в следующем: если функция задана неопределенным интегралом на интервале, то ее определенный интеграл на этом интервале можно вычислить, используя первообразную функцию и применяя основную теорему исчисления.
Таким образом, неопределенный интеграл позволяет находить первообразную функцию, а определенный интеграл — вычислять площадь, содержащуюся под кривой. Оба понятия взаимосвязаны и широко используются в различных областях математики и физики для решения задач и моделирования реальных явлений.
Функции Римана и разбиения отрезка
Функции Римана – это основной инструмент для определения значения определенного интеграла. Функции Римана представляют собой отмеченные отрезки, на которых значения функции принимаются внутри каждого отрезка и используются для вычисления интеграла.
В математике существуют различные способы разбиения отрезка. Наиболее распространенные из них – разбиение на равные части и разбиение на произвольные отрезки. При использовании разбиения на равные части, интервал интегрирования делится на равные по длине отрезки. При использовании разбиения на произвольные отрезки, интервал интегрирования делится на отрезки произвольной длины.
Значение определенного интеграла зависит от выбора разбиения отрезка и функции Римана. При более точном разбиении и выборе функции Римана, значение определенного интеграла будет приближаться к точному значению функции на интервале интегрирования.
Примером функции Римана может служить разбиение отрезка [a, b] на n равных частей, где значения функции на каждом отрезке принимаются в середине отрезка. Такое разбиение называется равномерным разбиением.
Таким образом, функции Римана и разбиения отрезка играют ключевую роль в определении значения определенного интеграла и помогают приблизить его точное значение.
Пределы Римана и сумма Римана
Пределы Римана представляют собой способ приближенного определения интеграла посредством разбиения области интегрирования на подотрезки и вычисления суммы значений функции на этих подотрезках. Процесс разбиения области интегрирования называется разбиением Римана.
Сумма Римана представляет собой сумму значений функции на подотрезках разбиения Римана, умноженных на соответствующие длины подотрезков. Сумму Римана можно использовать для приближенного вычисления значения интеграла.
Пределы Римана позволяют уточнить приближенное значение интеграла, уменьшая длину подотрезков разбиения и увеличивая их количество. Чем более точное приближение требуется, тем больше подотрезков разбиения необходимо использовать.
Сумма Римана может быть использована для приближенного вычисления значений интеграла, когда функция не может быть интегрирована аналитически. При увеличении числа подотрезков разбиения и уменьшении их длины, сумма Римана сходится к точному значению интеграла.
Интегрируемость функции на отрезке
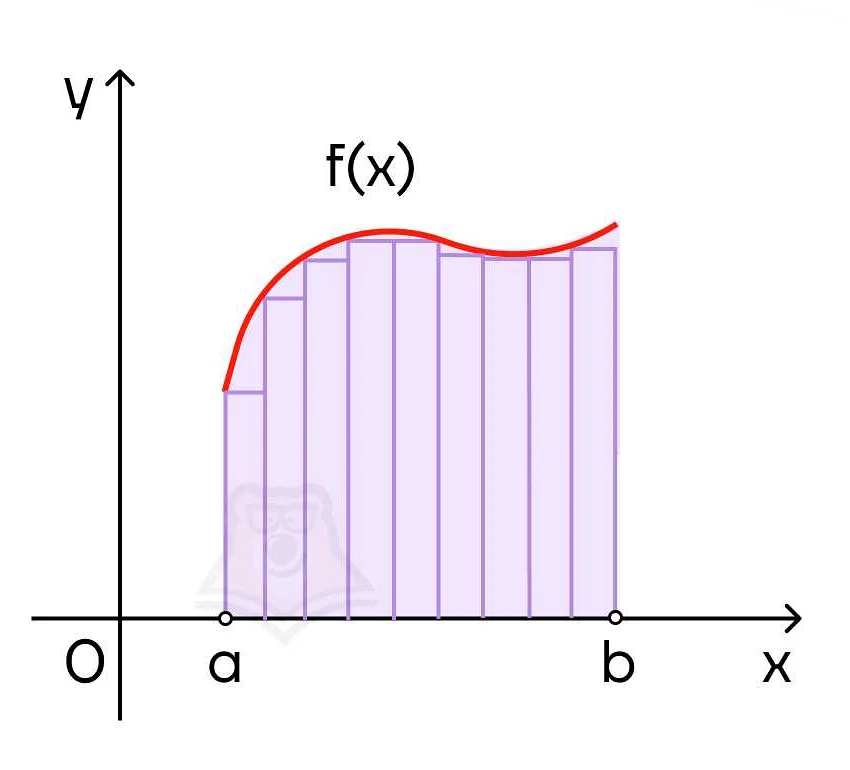
Функция называется интегрируемой на отрезке, если ее интеграл существует и конечен на этом отрезке. Для этого необходимо, чтобы функция была ограниченной на отрезке и имела лишь конечное число разрывов и точек разрыва первого рода.
Ограниченность функции означает, что существует такое число M, что для всех значений функции |f(x)| ≤ M на отрезке [a, b]. Это условие позволяет гарантировать конечность значения определенного интеграла.
Разрыв функции может быть либо устранимым, либо существенным. Устранимый разрыв возникает, когда функция имеет разрыв в одной или нескольких точках, но при этом существует предел функции в этих точках. Существенный разрыв возникает, когда предел функции в разрывной точке не существует.
Точка разрыва первого рода — это точка, в которой функция имеет разные пределы слева и справа от этой точки. Такие точки могут быть разрывами второго рода, если пределы отличаются более существенным образом.
Интегрируемость функции на отрезке позволяет использовать интегралы для решения различных задач. Например, вычисление площади фигуры под графиком функции на отрезке, определение среднего значения функции и т. д.
Основные свойства определенного интеграла
Определенный интеграл обладает несколькими важными свойствами, которые помогают в его вычислении и понимании:
1. Линейность: Если функции \(f(x)\) и \(g(x)\) интегрируемы на отрезке \([a, b]\) и \(c\) — произвольная константа, то
\[\int_{a}^{b} (f(x) + g(x)) \, dx = \int_{a}^{b} f(x) \, dx + \int_{a}^{b} g(x) \, dx\]
\[\int_{a}^{b} c \cdot f(x) \, dx = c \cdot \int_{a}^{b} f(x) \, dx\]
2. Аддитивность: Если функция \(f(x)\) интегрируема на отрезках \([a, c]\) и \([c, b]\), то
\[\int_{a}^{b} f(x) \, dx = \int_{a}^{c} f(x) \, dx + \int_{c}^{b} f(x) \, dx\]
3. Определенность: Определенный интеграл зависит от выбора границ интегрирования, а не от значения функции вне этих границ. Если функции \(f(x)\) и \(g(x)\) интегрируемы на отрезке \([a, b]\) и совпадают на всем этом отрезке, то
\[\int_{a}^{b} f(x) \, dx = \int_{a}^{b} g(x) \, dx\]
4. Обратимость: Если функция \(f(x)\) непрерывна на отрезке \([a, b]\) и интегрируема на нем, то
\[\int_{a}^{b} f(x) \, dx = -\int_{b}^{a} f(x) \, dx\]
Эти свойства позволяют более удобно и эффективно работать с определенными интегралами и использовать их для решения различных задач в математике и физике.
Примеры вычисления определенного интеграла
Определенный интеграл может быть вычислен с помощью различных методов, включая метод прямоугольников, метод тrapezoidal, метод Симпсона и т.д. Рассмотрим несколько примеров вычисления определенного интеграла:
Пример 1:
Вычислим определенный интеграл функции f(x) = x^2 на интервале от 0 до 2.
Сначала разделим интервал на равные части. В данном случае, мы выберем 4 равных части: 0-0.5, 0.5-1, 1-1.5 и 1.5-2.
Затем найдем значение функции f(x) в середине каждого подинтервала:
f(0.25) = (0.25)^2 = 0.0625
f(0.75) = (0.75)^2 = 0.5625
f(1.25) = (1.25)^2 = 1.5625
f(1.75) = (1.75)^2 = 3.0625
Затем, мы умножим каждое значение функции на ширину подинтервала (в данном случае, ширина подинтервала равна 0.5) и сложим полученные произведения:
(0.0625 * 0.5) + (0.5625 * 0.5) + (1.5625 * 0.5) + (3.0625 * 0.5) = 1.625
Таким образом, значение определенного интеграла функции f(x) = x^2 на интервале от 0 до 2 равно 1.625.
Пример 2:
Вычислим определенный интеграл функции f(x) = 2x + 3 на интервале от 1 до 3.
Для этого примера, мы будем использовать метод трапеций.
Сначала разделим интервал на равные части. В данном случае, мы выберем 4 равных части: 1-1.5, 1.5-2, 2-2.5 и 2.5-3.
Затем, мы найдем значение функции f(x) в концах каждого подинтервала:
f(1) = 2(1) + 3 = 5
f(1.5) = 2(1.5) + 3 = 6
f(2) = 2(2) + 3 = 7
f(2.5) = 2(2.5) + 3 = 8
Затем, мы умножим среднее значение функции на ширину подинтервала (в данном случае, ширина подинтервала равна 0.5) и сложим полученные произведения:
((5 + 6)/2 * 0.5) + ((6 + 7)/2 * 0.5) + ((7 + 8)/2 * 0.5) = 10.5
Таким образом, значение определенного интеграла функции f(x) = 2x + 3 на интервале от 1 до 3 равно 10.5.
Практическое применение определенного интеграла
Одним из наиболее распространенных применений определенного интеграла является вычисление площадей и объемов. Например, с помощью определенного интеграла можно вычислить площадь фигуры, ограниченной кривыми, или объем тела, образованного вращением кривой вокруг оси. Это находит применение в геометрии, физике, архитектуре и других областях.
Определенный интеграл также используется для вычисления средних значений функций. Например, с помощью интеграла можно найти среднюю скорость движения тела или среднюю температуру в определенный момент времени. Это имеет применение в физике, экономике, статистике и других областях.
Еще одним важным применением определенного интеграла является решение задачи о накоплении. Например, с помощью интеграла можно вычислить суммарный объем жидкости, протекающей через трубу за определенное время, или суммарное количество товара, проданного за определенный период. Это находит применение в экономике, физике, инженерии и других областях.
Также определенный интеграл используется для вычисления затрат и доходов. Например, с помощью интеграла можно вычислить затраты на производство или доход от продажи товара. Это имеет применение в экономике, бухгалтерии, финансах и других областях.
Таким образом, практическое применение определенного интеграла очень широко и включает множество различных областей. Благодаря его способности вычислять площади, объемы, средние значения и решать задачи о накоплении, определенный интеграл играет важную роль в практической математике и находит применение во многих сферах нашей жизни.
Видео по теме:
Что такое определенный интеграл?
Определенный интеграл — это одно из основных понятий математического анализа, которое позволяет находить площадь фигуры под графиком функции на заданном интервале.
Как вычислять определенный интеграл?
Для вычисления определенного интеграла используется метод Ньютона-Лейбница или метод интегрирования по частям. В общем случае, определенный интеграл вычисляется путем нахождения первообразной функции и подстановки границ интервала в это выражение.
Можно ли использовать определенный интеграл в других областях науки?
Определенный интеграл имеет широкое применение не только в математике, но и в других областях науки. Например, в физике он используется для вычисления площади под графиком скорости при постоянном ускорении, в экономике — для определения площади под графиком спроса или предложения, в биологии — для вычисления площади под кривой роста популяции и т.д.
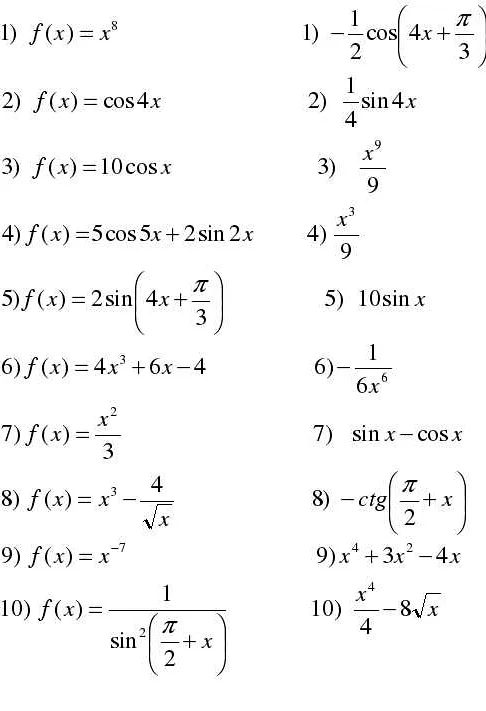



Статья очень понятно и доступно объясняет, что такое определенный интеграл в математике. Я всегда думала, что это сложное понятие, но благодаря этой статье я поняла, что определенный интеграл это просто площадь под графиком функции на заданном отрезке. Очень понравилось, как автор пошагово разъяснил основные понятия и привел примеры. Теперь я легко могу представить, как рассчитать определенный интеграл и какие при этом могут быть трудности. Эта информация наверняка будет полезна как студентам, так и всем, кто интересуется математикой. Большое спасибо автору за такую интересную и понятную статью!