Что такое комбинаторика в математике 10 класс

Узнайте, что такое комбинаторика в математике для 10 класса: основные понятия, методы и примеры. Изучайте комбинаторные задачи и развивайте свои навыки решения задач.

Комбинаторика – важная раздел математики, изучающая методы подсчета числа комбинаций и перестановок. Эта наука помогает решать различные задачи, связанные с выбором и расположением элементов в различных объектах, таких как наборы, множества, графы и другие структуры. Комбинаторика широко применяется во многих областях, включая информатику, статистику, теорию вероятностей, криптографию и даже в играх.

Основные принципы комбинаторики включают: принцип суммы, принцип умножения, принцип Дирихле и принцип Дополнения. Принцип суммы гласит, что чтобы посчитать общее число исходов, нужно сложить числа исходов каждого отдельного случая. Принцип умножения говорит о том, что чтобы посчитать число исходов последовательных событий, нужно перемножить числа исходов каждого события.

Принцип Дирихле утверждает, что если n+1 объектов размещены в n местах, то как минимум одно место должно быть занято дважды. Принцип Дополнения позволяет сосчитать число исключающих событий путем вычитания количества исходов события, которое хотим исключить, из общего числа возможных исходов.

Знание комбинаторики необходимо для успешного решения множества задач на олимпиадах по математике, а также для понимания основных понятий в других областях математики. Понимание комбинаторики помогает развивать логическое мышление, аналитические навыки и способность к абстрактному мышлению.

Основные понятия комбинаторики

В комбинаторике используется несколько основных понятий, которые помогают в описании и анализе различных комбинаторных задач. Некоторые из этих понятий включают:

ПонятиеОписание

Перестановка	Упорядоченный набор объектов без повторений.
Сочетание	Неупорядоченный набор объектов без повторений.
Размещение	Упорядоченный набор объектов с повторениями.
Сочетание с повторениями	Неупорядоченный набор объектов с повторениями.

Эти основные понятия комбинаторики позволяют решать различные задачи, связанные с выбором, упорядочиванием и учетом объектов. Комбинаторика находит применение во многих областях, включая теорию вероятности, алгебру, криптографию, компьютерные науки и другие.

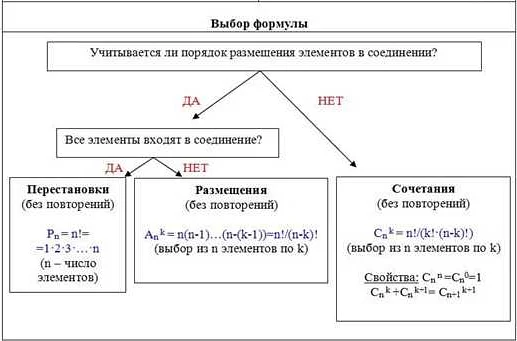
Размещения и перестановки

Размещения — это упорядоченные наборы элементов из заданного множества. Когда порядок элементов имеет значение, размещения используются для подсчета количества возможных вариантов расположения элементов. Формула для подсчета количества размещений обычно записывается как Ank, где n — количество элементов в множестве, а k — количество элементов в каждом наборе.

Перестановки — это упорядоченные наборы элементов из заданного множества, где каждый элемент может использоваться только один раз. Перестановки используются для подсчета количества возможных вариантов перестановки элементов в множестве. Формула для подсчета количества перестановок обычно записывается как Pn, где n — количество элементов в множестве.

Понимание и применение размещений и перестановок позволяет решать широкий диапазон задач, связанных с подсчетом комбинаций и упорядочиванием элементов.

Сочетания без повторений и с повторениями

Сочетания – это комбинации элементов из данного множества без учета порядка и без повторений. Сочетаниями обычно называются подмножества заданного множества. Сочетания без повторений – это такие сочетания, в которых элементы не могут повторяться. Например, если имеется множество {A, B, C}, то возможными сочетаниями без повторений будут {A, B}, {A, C} и {B, C}.

Сочетания с повторениями – это комбинации элементов из данного множества без учета порядка, но с возможностью повторения элементов. Например, если имеется множество {A, B, C}, то возможными сочетаниями с повторениями будут {A, A}, {A, B}, {A, C}, {B, B}, {B, C}, {C, C} и так далее.

Для расчета количества сочетаний без повторений и с повторениями существуют специальные формулы и принципы, которые позволяют определить число возможных комбинаций и перестановок. Эти знания являются важными для решения задач в различных областях, таких как теория вероятностей, информатика, экономика и другие.

Правило суммы и правило произведения

Правило суммы гласит, что если для выполнения некоторого действия имеются n способов, а для выполнения другого действия имеются m способов, то всего имеется n + m способов выполнить одно из этих действий.

Например, если у нас есть две одинаковые коробки с шарами, в первой коробке находится n шаров, а во второй — m шаров, то всего есть n + m способов выбрать шар из одной из коробок.

Правило произведения позволяет определить, сколько всего вариантов возможно, если для выполнения одного действия имеется n способов, а для выполнения другого действия имеется m способов.

Например, если у нас есть 3 разных краски и 4 разных кисти, то всего существует 3 * 4 = 12 способов выбрать краску и кисть для рисования.

Правила суммы и произведения широко применяются в комбинаторике для решения задач, связанных с подсчетом комбинаций, перестановок и сочетаний. Они позволяют систематизировать и анализировать возможности выбора и расположения элементов в задачах комбинаторики.

Принцип Дирихле и принцип включения-исключения

Принцип Дирихле находит свое применение во многих областях математики, физики, информатики и других науках. Он позволяет доказывать существование определенных объектов и связей между ними.

Принцип включения-исключения – это еще один важный принцип комбинаторики, который используется для подсчета объединений и пересечений множеств. Он позволяет находить количество элементов в объединении или пересечении нескольких множеств.

Принцип включения-исключения формулируется следующим образом: если имеются несколько множеств, то количество элементов в их объединении равно сумме количеств элементов в каждом множестве, минус количество элементов в пересечении каждой пары множеств, плюс количество элементов в пересечении каждой тройки множеств, и так далее.

Принцип включения-исключения является мощным инструментом для решения задач комбинаторики и позволяет учитывать различные комбинации объектов и их взаимодействия.

Видео по теме:

Вопрос-ответ:

Что такое комбинаторика?

Комбинаторика — это раздел математики, который изучает комбинаторные структуры и методы их исследования. Она занимается подсчетом и анализом способов размещения, сочетания и перестановки элементов в различных комбинаторных задачах.

Какие основные принципы комбинаторики существуют?

Основные принципы комбинаторики включают принципы умножения, сложения, включения-исключения, беспорядка и Дирихле.

Как применяются комбинаторные задачи в реальной жизни?

Комбинаторика имеет практическое применение в различных областях, таких как криптография, компьютерная наука, оптимизация, статистика, генетика, экономика и другие. Например, комбинаторика может быть использована для прогнозирования вероятностей, составления расписаний, проектирования кодов связи и многих других задач.

Какие методы используются для решения комбинаторных задач?

Для решения комбинаторных задач используются различные методы, включая методы перебора, принципы комбинаторики, принцип Дирихле, принцип включения-исключения и другие. В зависимости от задачи, выбирается наиболее подходящий метод решения.

Что такое размещение, сочетание и перестановка элементов?

Размещение — это упорядоченная выборка элементов из множества без повторений; сочетание — это неупорядоченная выборка элементов из множества без повторений; перестановка — это упорядоченная выборка элементов из множества с повторениями или без повторений.

Биномиальный коэффициент и треугольник Паскаля

${n \choose k} = \frac{n!}{k!(n-k)!}$, где $n!$ — факториал числа n.

Биномиальный коэффициент можно интерпретировать как количество способов выбрать k элементов из n без учета порядка. Например, ${5 \choose 2} = \frac{5!}{2!(5-2)!} = \frac{5 \cdot 4}{2 \cdot 1} = 10$, что означает, что из 5 элементов можно выбрать 2 элемента 10 различными способами.

Одним из способов представления биномиального коэффициента является треугольник Паскаля. Треугольник Паскаля — это числовой треугольник, в котором каждое число равно сумме двух чисел над ним. Первая строка треугольника состоит из единицы, а каждый следующий элемент в строке получается путем сложения двух соседних элементов из предыдущей строки.

Пример треугольника Паскаля:

• 1
• 1 1
• 1 2 1
• 1 3 3 1
• 1 4 6 4 1
• …

Каждое число в треугольнике Паскаля соответствует биномиальному коэффициенту. Например, в третьей строке треугольника Паскаля числа 1 2 1 соответствуют ${2 \choose 0}$, ${2 \choose 1}$ и ${2 \choose 2}$ соответственно.

Применение комбинаторики в жизни и науке

1. Криптография. Комбинаторика играет важную роль в разработке криптографических алгоритмов и систем защиты информации. Например, комбинаторные методы используются для создания сложных паролей, генерации случайных чисел и шифрования данных.
2. Телекоммуникации. В сфере телекоммуникаций комбинаторика применяется для оптимизации работы сетей передачи данных, разработки алгоритмов сжатия информации и кодирования сигналов.
3. Искусственный интеллект. В области искусственного интеллекта комбинаторика используется для решения задач планирования, оптимизации и принятия решений. Например, комбинаторные методы могут помочь определить оптимальный маршрут для робота-манипулятора или найти наилучший вариант решения задачи.
4. Биология. В биологии комбинаторика применяется для изучения генетического кода и моделирования молекулярных структур. Комбинаторные методы позволяют анализировать различные варианты комбинаций генов и предсказывать их воздействие на организм.
5. Финансы и экономика. В финансовой и экономической сферах комбинаторика используется для моделирования рынков, анализа портфелей инвестиций и определения оптимальных стратегий. Комбинаторные методы помогают прогнозировать поведение рынка и принимать обоснованные финансовые решения.

Это лишь некоторые примеры применения комбинаторики в жизни и науке. Разработка новых комбинаторных методов и исследование комбинаторных объектов продолжается, что открывает новые возможности применения этого раздела математики в различных областях.