Что такое комбинаторика в математике

Что такое комбинаторика в математике? Узнайте основные концепции и принципы этой важной области математики, которая изучает комбинаторные структуры и подсчитывает количество возможных комбинаций и перестановок. Познакомьтесь с основными терминами и методами комбинаторики, такими как сочетания, перестановки, размещения и многое другое.

Комбинаторика – это раздел математики, изучающий количественные аспекты комбинаторных объектов и их свойства. В комбинаторике рассматриваются различные способы счета и упорядочивания объектов, а также применение этих методов для решения различных задач.

Одним из основных принципов комбинаторики является принцип умножения. Он утверждает, что если есть два независимых события, которые могут произойти в различных вариантах, то количество возможных исходов обоих событий можно получить, умножив количество вариантов первого события на количество вариантов второго события. Этот принцип активно используется при решении задач на размещение и сочетание элементов.

Примером использования принципа умножения может служить задача о выборе одежды. Предположим, у нас есть 3 футболки и 2 шорта. Если мы хотим выбрать одну футболку и одни шорты, то по принципу умножения получаем, что всего существует 3 * 2 = 6 вариантов комбинаций.

Кроме принципа умножения, в комбинаторике существует также принцип сложения. Он утверждает, что если есть несколько независимых событий, которые могут произойти взаимоисключающими способами, то количество возможных исходов всех этих событий можно получить, сложив количество вариантов каждого события. Этот принцип часто применяется при решении задач на разбиение объектов на классы или группы.

Комбинаторика является важным инструментом в различных областях науки и техники. Она находит применение в теории вероятностей, криптографии, логике, компьютерных науках, теории игр и других дисциплинах. Знание основ и принципов комбинаторики позволяет более эффективно решать задачи, связанные с подсчетом и упорядочиванием объектов.

Основные понятия комбинаторики

Основными понятиями комбинаторики являются:

1. Факториал — это операция, которая позволяет посчитать количество возможных перестановок элементов множества. Факториал числа n (обозначается как n!) равен произведению всех чисел от 1 до n.

2. Комбинация — это упорядоченный набор элементов, выбранных из заданного множества. Количество комбинаций можно вычислить с помощью сочетаний без повторений. Комбинация из n элементов по k выбирается из множества, содержащего n элементов, и не учитывает порядок выбранных элементов.

3. Перестановка — это упорядоченное расположение элементов множества. Перестановки можно вычислить с помощью факториала. Перестановка из n элементов равна n!.

4. Размещение — это упорядоченный набор элементов, выбранных из заданного множества без повторений. Размещение из n элементов по k выбирается из множества, содержащего n элементов, и учитывает порядок выбранных элементов.

5. Биномиальный коэффициент — это число, которое определяет количество комбинаций из n элементов по k. Биномиальный коэффициент обозначается символом C(n,k) и вычисляется по формуле C(n,k) = n! / (k!(n-k)!).

Основные понятия комбинаторики позволяют решать широкий спектр задач, связанных с подсчетом и упорядочиванием объектов. Знание этих понятий является важным для понимания и применения комбинаторных методов и принципов в различных областях науки и практических задачах.

Видео по теме:

Сочетания и перестановки

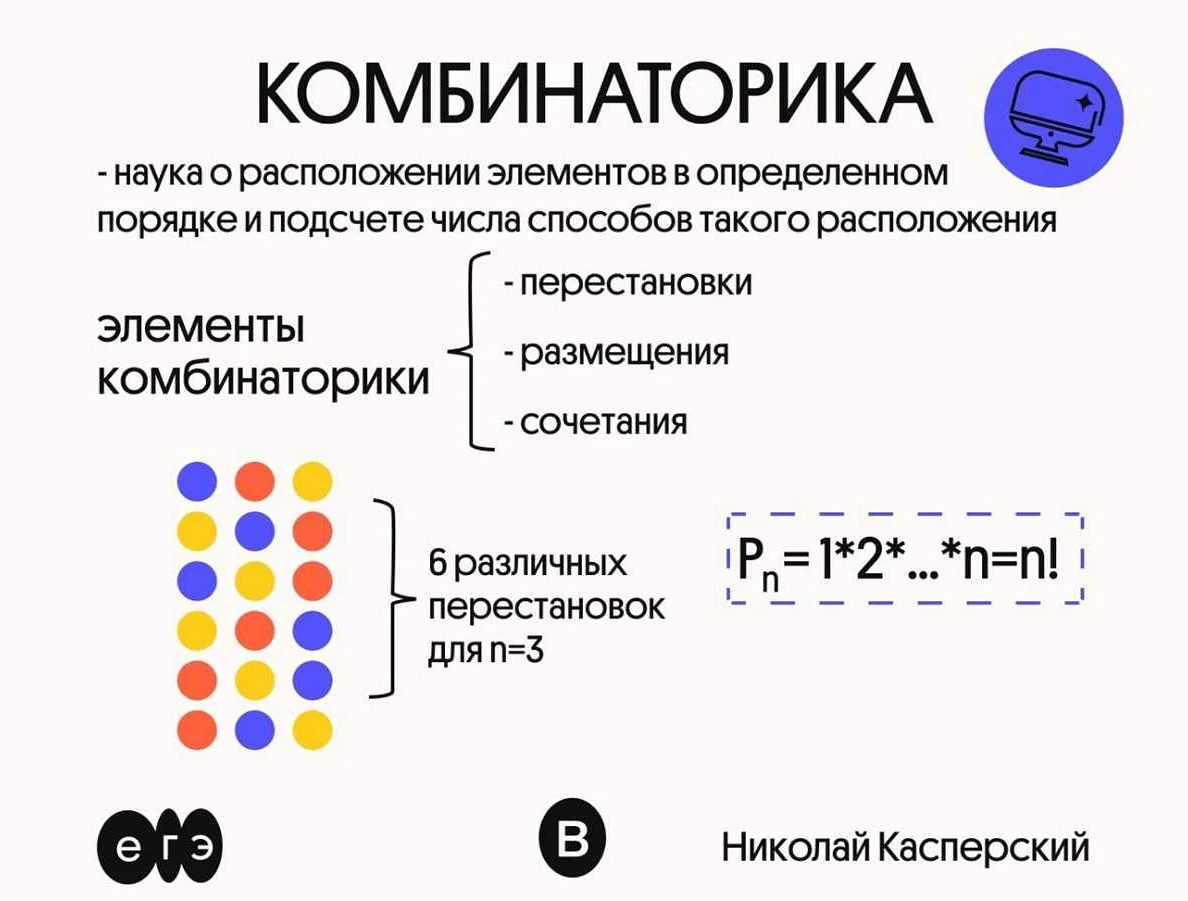
Перестановки — это все возможные способы, которыми можно упорядочить элементы заданного множества. Если имеется множество из n элементов, то количество перестановок будет равно n! (n факториал). Например, для множества из 3 элементов будет 3! = 3 * 2 * 1 = 6 перестановок.

Сочетания — это все возможные способы выбрать k элементов из заданного множества, где порядок не имеет значения. Количество сочетаний можно вычислить по формуле C(n, k) = n! / (k! * (n-k)!). Например, если имеется множество из 5 элементов, и мы хотим выбрать 3 элемента, то количество сочетаний будет C(5, 3) = 5! / (3! * 2!) = 10.

Знание сочетаний и перестановок позволяет решать различные задачи, связанные с выбором элементов и их упорядочиванием. Эти понятия играют важную роль не только в математике, но и в других областях, таких как теория вероятности, статистика, информатика и др.

Принцип умножения

Принцип умножения формулируется следующим образом: если есть n способов выполнить первое действие и m способов выполнить второе действие, то общее количество вариантов комбинаций равно произведению n и m.

Этот принцип находит применение во многих областях, таких как теория вероятностей, комбинаторика, алгебра и другие.

Для лучшего понимания принципа умножения можно представить следующий пример: если у нас есть 2 рубашки (красная и синяя) и 3 пары штанов (черные, синие и серые), то общее количество возможных комбинаций рубашек и штанов будет равно 2 умножить на 3, то есть 6. Мы можем получить следующие комбинации: красная рубашка с черными штанами, красная рубашка с синими штанами, красная рубашка с серыми штанами, синяя рубашка с черными штанами, синяя рубашка с синими штанами и синяя рубашка с серыми штанами.

Вопрос-ответ:

Зачем изучать комбинаторику?

Изучение комбинаторики позволяет решать задачи, связанные с подсчетом количества объектов или различных их комбинаций. Эта область математики находит применение в различных науках и областях жизни, таких как информатика, статистика, экономика, физика и другие. Обучение комбинаторике развивает логическое мышление, аналитические навыки и способность решать сложные задачи.

Какие основные принципы комбинаторики?

В комбинаторике существует несколько основных принципов. Это принцип перестановок, принцип комбинаций и принцип умножения. Принцип перестановок используется для подсчета количества возможных перестановок элементов, принцип комбинаций — для подсчета комбинаций элементов, а принцип умножения — для подсчета количества возможных исходов последовательных действий.

Что такое факториал?

Факториал — это математическая функция, которая определяется для натуральных чисел. Факториал числа n обозначается символом n! и равен произведению всех натуральных чисел от 1 до n. Например, факториал числа 5 равен 5! = 5 * 4 * 3 * 2 * 1 = 120. Факториал используется в комбинаторике для подсчета количества возможных перестановок элементов.

Как применяется комбинаторика в информатике?

Комбинаторика играет важную роль в информатике. Она используется для решения задач связанных с подсчетом количества возможных комбинаций и перестановок элементов, а также для оптимизации алгоритмов и разработки кодирования информации. Например, комбинаторика используется при разработке алгоритмов сортировки, поиска, генерации случайных чисел и других задач информатики.

Принцип сложения

Согласно принципу сложения, если происходят два независимых события, то общее количество исходов равно сумме количества исходов каждого из событий. То есть, если событие A может произойти m способами, а событие B может произойти n способами, то общее количество исходов будет равно m + n.

Например, если у нас есть две различные задачи, которые мы можем решить независимо друг от друга – задача А и задача В, и каждую из этих задач мы можем решить двумя способами, то общее количество способов решить обе задачи будет равно 2 + 2 = 4.

Принцип сложения можно применять не только к двум событиям, но и к любому количеству независимых событий. В этом случае общее количество исходов будет равно сумме количества исходов каждого события.

Биномиальные коэффициенты

Биномиальные коэффициенты обозначаются символом C(n, k) и вычисляются по формуле:

C(n, k) = n! / (k!(n — k)!),

где n — количество элементов в множестве, из которого берутся комбинации, а k — количество элементов в каждой комбинации.

Биномиальные коэффициенты имеют много полезных свойств. Они, например, позволяют находить количество способов выбрать или разместить объекты, а также находить вероятность различных событий. Биномиальные коэффициенты также связаны с разложением бинома Ньютона и являются коэффициентами в разложении биномиальной степени.

Использование биномиальных коэффициентов позволяет решать задачи, связанные с подсчетом комбинаторных объектов, таких как сочетания, перестановки, размещения, разбиения и другие. Они находят применение в таких областях, как теория вероятностей, теория чисел, алгебра, комбинаторика и дискретная математика.

Треугольник Паскаля

Треугольник Паскаля обладает множеством интересных свойств и находит применение в различных областях математики, физики, информатики и других науках.

Треугольник Паскаля имеет следующую структуру: каждый ряд треугольника начинается и заканчивается числом 1, а остальные числа рассчитываются путем сложения двух чисел, расположенных над ним, в предыдущем ряду. Например, второй ряд треугольника Паскаля выглядит следующим образом:

1
1	1

Третий ряд будет выглядеть так:

1
1	1
1	2	1

И так далее. Каждое число в треугольнике Паскаля представляет собой количество способов выбрать определенное количество элементов из множества. Например, в третьем ряду треугольника число 2 означает, что есть два способа выбрать 1 элемент из множества из 3 элементов.

Треугольник Паскаля также обладает симметричной структурой относительно его центральной оси, что делает его очень удобным инструментом для решения задач комбинаторики, вычисления биномиальных коэффициентов и других математических операций.

Принцип Дирихле

Принцип Дирихле получил широкое применение в различных областях математики и информатики. Он позволяет формулировать и доказывать различные утверждения, связанные с распределением объектов по ячейкам.

Простейший пример применения принципа Дирихле – это задача о разделении n+1 элементов по n ячейкам. Если каждый элемент размещается в отдельной ячейке, то, согласно принципу Дирихле, хотя бы одна ячейка будет содержать два элемента.

Принцип Дирихле широко используется в комбинаторике для решения задач, связанных с перестановками, сочетаниями и размещениями. Например, он позволяет доказывать существование повторений в последовательности элементов и определять количество возможных вариантов распределения объектов.