Что такое краткое в математике 6 класс

Кратное в математике 6 класс — это число, которое делится на другое число без остатка. Узнайте, как определить кратность числа, используя простые правила и примеры.

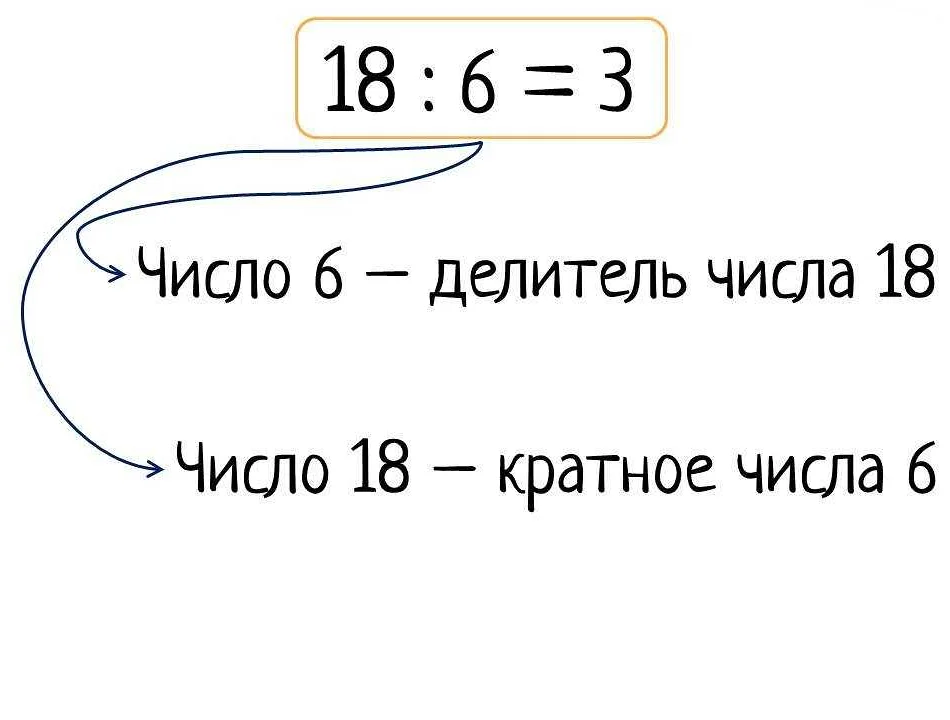
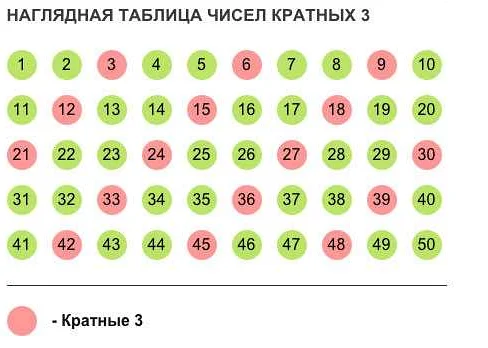
Кратные числа – это числа, которые можно получить путем умножения другого числа на некоторую константу. Такие числа имеют множество общих делителей с этим числом, и их сумма или разность также являются кратными числами. Например, числа 6, 12, 18 и 24 являются кратными числами числа 3, так как они получаются путем умножения числа 3 на 2, 4, 6 и 8 соответственно.

Кратность числа – это количество повторений этого числа в последовательности кратных чисел. Например, число 6 кратно числу 3 и имеет кратность 4, так как 6 встречается 4 раза в последовательности чисел 3, 6, 9, 12, 15 и т.д.

Пример:

Для того чтобы найти кратные числа числа 4, нужно умножать его на целые числа. Так, кратные числа числа 4 будут: 4, 8, 12, 16, 20 и т.д.

Знание кратных чисел и понимание их свойств позволяют решать различные задачи и упрощать вычисления в математике. Кроме того, понимание кратных чисел помогает в изучении других математических тем, таких как дроби, десятичные дроби и десятичные десятичные числа.

Что такое краткое в математике 6 класс

Рассмотрим пример: пусть у нас есть числа 4 и 8. Кратные числа для 4 и 8 будут 4, 8, 12, 16, 20 и так далее. В данном случае, общими делителями для 4 и 8 являются числа 4 и 8.

Кратные числа могут быть положительными, отрицательными или нулем. Кратные числа также могут быть представлены формулой: n * k = m, где n и k — числа, а m — кратное число.

Знание понятия кратного числа в математике 6 класса поможет ученикам лучше понять операции с числами, разложение на множители, а также решение уравнений и задач.

Видео по теме:

Определение и суть понятия

Суть понятия краткого заключается в том, что мы опускаем столбцы, в которых нет ненулевых цифр, и заменяем их нулями. Например, число 205, в котором нулей нет, можно записать в краткой форме как 2,05. В этом случае, ноль вместо столбца сотен показывает, что в числе нет сотен.

Краткое представление десятичных чисел позволяет упростить математические вычисления, так как убирает несущественные нули и уменьшает объем записи числа. Например, при умножении или делении чисел, записанных в краткой форме, не нужно учитывать нулевые столбцы, что делает вычисления более простыми и быстрыми.

Примеры краткого в математике

1. Краткое деление: оно используется для деления одного числа на другое. Например, если нужно разделить 36 на 4, то запись будет выглядеть так:

9

4|36

-36

0

Результат деления 36 на 4 равен 9.

2. Краткое умножение: это операция умножения двух чисел. Например, если нужно перемножить 6 и 7, запись будет выглядеть так:

6

x 7

______

42

Результат умножения 6 на 7 равен 42.

3. Краткое вычитание: оно используется для вычитания одного числа из другого. Например, если нужно вычесть 15 из 26, запись будет выглядеть так:

26

-15

____

11

Результат вычитания 15 из 26 равен 11.

4. Краткое сложение: это операция сложения двух чисел. Например, если нужно сложить 8 и 9, запись будет выглядеть так:

8

+ 9

____

17

Результат сложения 8 и 9 равен 17.

Вопрос-ответ:

Что такое краткое в математике 6 класс?

Краткое – это число, которое делится нацело на другое число, не оставляя остатка. Например, кратное числу 3 это 3, 6, 9, 12 и т.д.

Как определить, является ли число кратным другому числу?

Чтобы определить, является ли число кратным другому числу, нужно проверить, делится ли оно нацело на это число. Если делится без остатка, то число является кратным, а если остаток есть, то число не является кратным.

Какие примеры кратных чисел можно привести?

Например, числа 10, 20, 30 и т.д. являются кратными числу 10, так как они делятся нацело на 10. Также, числа 8, 16, 24 и т.д. являются кратными числу 8, так как они делятся нацело на 8.

Как найти наименьшее кратное двух чисел?

Чтобы найти наименьшее кратное двух чисел, нужно найти их наименьшее общее кратное (НОК). Для этого следует разложить оба числа на простые множители и умножить их общие и необщие простые множители в наибольших степенях.

Как найти кратное числа?

Чтобы найти кратное числа, нужно умножить это число на любое другое число. Например, чтобы найти кратное числа 4, можно умножить его на 2 и получить число 8, которое является кратным числа 4.

Значение и применение в повседневной жизни

Понятие краткого в математике имеет большое значение и применение в повседневной жизни. Краткое числовое выражение помогает нам быстро и удобно записывать и решать различные математические задачи.

Например, представим ситуацию, когда нам нужно посчитать сумму денег, которую мы потратили на покупку продуктов в магазине. Вместо того, чтобы записывать все цены на продукты по отдельности, мы можем использовать краткое выражение, например, «10 + 15 + 20 + 5», где каждое число представляет сумму, потраченную на каждый продукт. Таким образом, мы можем быстро и легко рассчитать общую сумму потраченных денег.

Краткое в математике также помогает нам решать задачи, связанные с временем. Например, если нам нужно посчитать, сколько времени мы провели на занятиях по разным предметам, мы можем использовать краткое выражение, например, «1 + 2 + 1.5 + 0.5», где каждое число представляет количество часов, затраченных на каждый предмет. Таким образом, мы можем легко определить, сколько времени мы потратили на учебу в целом.

Краткое в математике также находит применение в финансовых расчетах, статистике, геометрии и многих других областях повседневной жизни. Оно позволяет нам удобно и точно выражать различные математические операции и решать разнообразные задачи.

Роль краткого в изучении алгебры

Краткое может быть использовано для представления различных математических операций, таких как сложение, вычитание, умножение и деление многочленов. Оно позволяет увидеть общую структуру и особенности многочленов, что помогает в решении уравнений и систем уравнений.

Например, при работе с кратким в алгебре можно использовать такие понятия, как коэффициенты, степени и члены многочленов. Коэффициенты определяют числовую часть каждого члена, степень показывает степень переменной в каждом члене, а члены являются отдельными слагаемыми в многочлене.

Использование краткого в изучении алгебры позволяет упростить вычисления и анализ многочленов, а также облегчает понимание основных понятий и методов алгебры. Оно является важным инструментом для решения различных задач и задачек, которые встречаются в школьной программе по математике.

Сравнение краткого с другими математическими понятиями

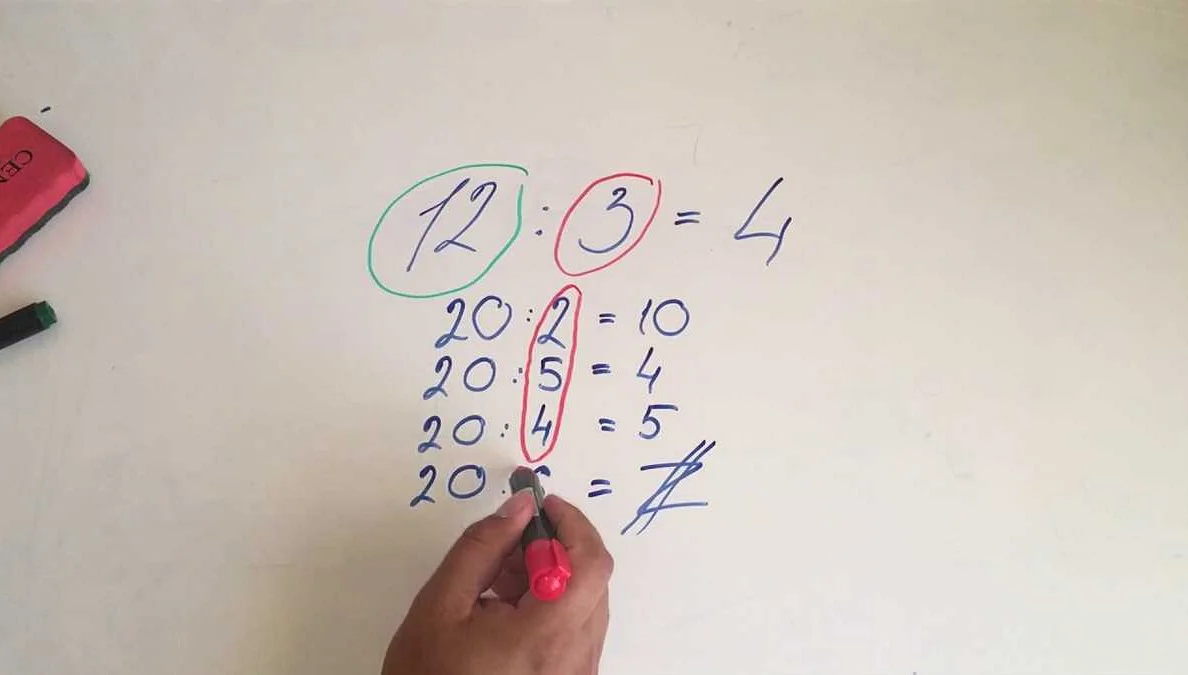
Краткое — это результат деления одного числа на другое, когда делитель полностью делит делимое. В отличие от суммы, разности, произведения и частного, краткое является результатом операции деления и всегда будет меньше или равно делимому.

Например, если мы хотим найти краткое числа 20 на 5, мы делим 20 на 5 и получаем результат 4. Это означает, что 20 делится на 5 четыре раза без остатка.

В отличие от краткого, сумма двух чисел — это результат их сложения. Например, сумма чисел 3 и 5 равна 8.

Разность двух чисел — это результат их вычитания. Например, разность чисел 8 и 3 равна 5.

Произведение двух чисел — это результат их умножения. Например, произведение чисел 4 и 5 равно 20.

Частное двух чисел — это результат их деления. Например, частное чисел 15 и 3 равно 5.

Таким образом, краткое отличается от других математических понятий, таких как сумма, разность, произведение и частное, тем, что оно всегда будет меньше или равно делимому и является результатом операции деления.

Обучение краткому в школе

На уроках математики в 6 классе ученики изучают различные способы использования краткого. Они учатся сокращать дроби, записывать числа в научной нотации, вычислять выражения с использованием приоритетов операций, и многое другое.

Один из примеров использования краткого в математике – запись десятичных чисел с помощью десятичной точки. Например, число 3,141592653589793 может быть записано как π. Это упрощает запись и запоминание числа и используется во многих формулах и уравнениях.

Другой пример – использование индексов для обозначения степени числа. Например, число 2 в квадрате может быть записано как 2². Это позволяет более компактно и ясно указать, что число нужно возвести в степень.

Умение использовать краткое в математике помогает ученикам более эффективно работать с числами и операциями, а также развивает их логическое мышление и аналитические навыки.

Использование краткого в решении задач

Использование краткого позволяет упростить задачу и сделать ее решение более понятным и логичным. Задачи, решаемые с помощью краткого, часто сводятся к нахождению значения неизвестных величин или выражений.

Примером использования краткого может быть задача: «Число увеличили на 15, затем полученный результат уменьшили в 3 раза. Получилось число 36. Найдите исходное число».

При использовании краткого в решении этой задачи можно обозначить исходное число буквой «х». Тогда условие задачи можно записать следующим образом: «х + 15» (увеличили на 15) «х + 15 — 3х» (уменьшили в 3 раза) «36» (получилось число 36).

Далее, решение сводится к нахождению значения буквенной обозначенной «х». Для этого нужно разрешить получившееся уравнение: «х + 15 — 3х = 36». Решив это уравнение, можно найти искомое значение «х».

Таким образом, использование краткого позволяет перевести задачу на язык алгебры и найти ее решение с помощью алгебраических операций.