Определение кратности в математике простыми словами и его применение
Содержимое
- 1 Определение кратности в математике простыми словами и его применение
- 1.1 Кратное в математике: определение и основные понятия
- 1.2 Что такое кратное числа и кратность?
- 1.3 Как найти кратное число?
- 1.4 Примеры кратных чисел
- 1.5 Свойства кратных чисел
- 1.6 Кратность чисел в арифметических операциях
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
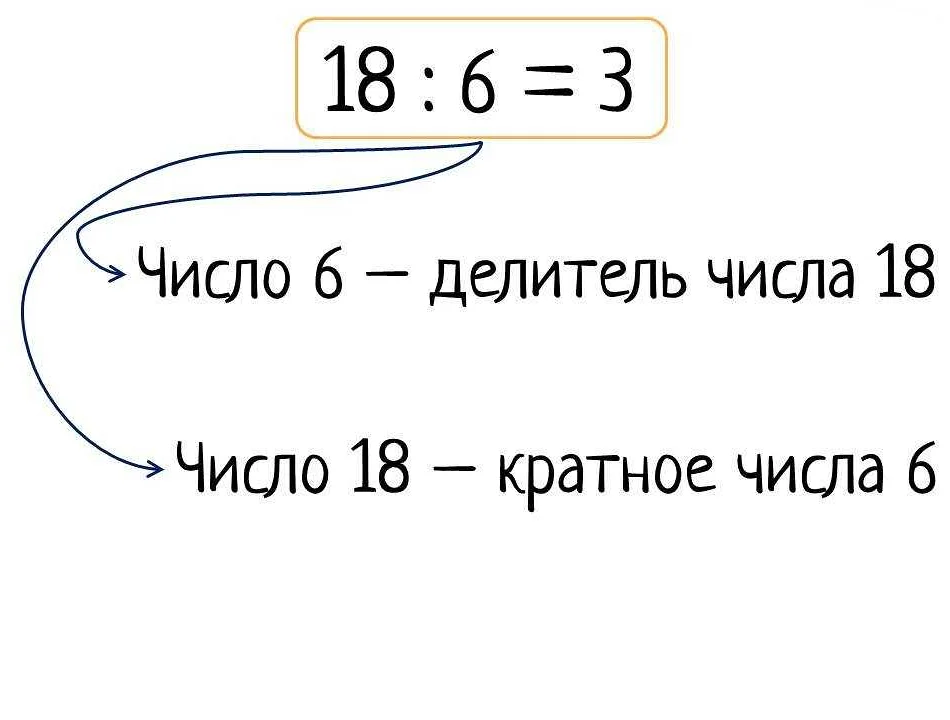
- 1.9 Кратное число и делители
- 1.10 Применение кратных чисел в реальной жизни
Кратное в математике – это число, которое делится на другое число без остатка. Узнайте, как определить кратность числа и как использовать это понятие в различных математических задачах.
Кратное в математике — это число, которое делится на другое число без остатка. Например, если число 12 делится на число 3 без остатка, то говорят, что 12 кратно 3. В этом случае, 3 является делителем, а 12 — кратным числом. Кратными числами также называются все числа, которые можно получить путем умножения данного числа на целое число.
Другими словами, если число A делится на число B без остатка, то говорят, что A кратно B. Например, число 15 кратно числу 5, потому что 15 делится на 5 без остатка. Также можно сказать, что 15 кратно 3, так как 15 делится на 3 без остатка.
Кратность является важным понятием в математике, так как она позволяет решать множество задач и упрощает работу с числами. Например, если нам нужно найти все числа, которые кратны одновременно 2, 3 и 5, мы можем использовать понятие НОК (наименьшее общее кратное) и найти наименьшее число, которое делится без остатка на все эти числа.
Таким образом, понятие кратного числа позволяет упростить работу с делением нацело и решать различные задачи, связанные с числами.
Кратное в математике: определение и основные понятия

Например, число 12 является кратным числа 3, потому что 12 делится на 3 без остатка. Также, число 30 является кратным числа 5, потому что 30 делится на 5 без остатка.
Для определения кратности числа в математике используется понятие «деление с остатком». Если при делении одного числа на другое, остаток равен нулю, то первое число считается кратным второго.
Кратные числа можно представить в виде таблицы, где каждая строка представляет собой число, а каждый столбец — его кратное.
ЧислоКратное 1Кратное 2Кратное 3
| 1 | 1 | 2 | 3 |
| 2 | 2 | 4 | 6 |
| 3 | 3 | 6 | 9 |
Из таблицы видно, что числа 2 и 4 являются кратными числа 2, так как они делятся на 2 без остатка. А числа 3 и 9 являются кратными числа 3, так как они делятся на 3 без остатка.
Кратные числа имеют своеобразные свойства и используются в различных областях математики, физики, программирования и других научных дисциплинах.
Что такое кратное числа и кратность?
Кратность — это количество раз, которое одно число содержится в другом числе. Например, число 12 имеет кратность 3 по отношению к числу 4, так как 12 содержит число 4 три раза: 4, 8 и 12.
Кратность числа может быть положительной или нулевой, но не может быть отрицательной. Например, число 10 кратно числу 5 и имеет кратность 2, так как 10 содержит число 5 два раза: 5 и 10.
Кратность числа может быть использована для решения различных задач, например, для определения общего кратного двух или более чисел или для определения делителей числа.
Итак, кратное числа — это число, которое делится на другое число без остатка, а кратность — это количество раз, которое одно число содержится в другом числе.
Как найти кратное число?
Шаг 1: Определите число, для которого вы хотите найти кратное число.
Шаг 2: Выберите число, на которое вы хотите делить исходное число.
Шаг 3: Разделите исходное число на выбранное число. Если остаток от деления равен нулю, то исходное число является кратным числом.
Шаг 4: Если остаток от деления не равен нулю, увеличьте исходное число на выбранное число и повторите шаг 3.
Например, если вы хотите найти кратное число для числа 6, и выберите число 3 для деления, то:
6 / 3 = 2, остаток равен 0, значит 6 — кратное число для числа 3.
Если остаток не равен нулю, например:
6 / 4 = 1,5, остаток не равен 0. Увеличим число 6 на 4 и продолжим деление:
10 / 4 = 2,5, остаток не равен 0. Увеличим число 10 на 4 и продолжим деление:
14 / 4 = 3,5, остаток не равен 0. Увеличим число 14 на 4 и продолжим деление:
18 / 4 = 4,5, остаток не равен 0. И так далее, пока не получите остаток равный 0.
Таким образом, вы можете найти кратное число для любого числа, выбрав подходящее число для деления и выполнив деление с увеличением исходного числа, если остаток не равен нулю.
Примеры кратных чисел
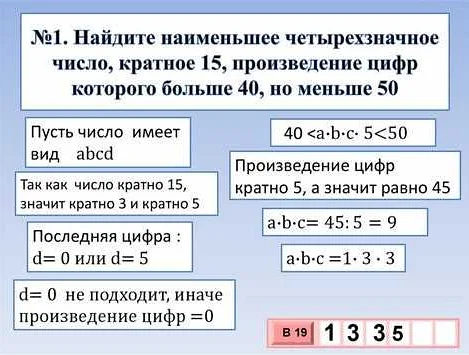
Кратными числами называются числа, которые делятся на другое число без остатка. Например, число 10 кратно числу 5, так как 10 можно разделить на 5 и получить целое число 2.
Вот еще несколько примеров кратных чисел:
Кратные числа числа 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…
Кратные числа числа 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…
Кратные числа числа 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40…
Кратные числа числа 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50…
Кратные числа числа 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100…
Таким образом, кратные числа образуют бесконечные последовательности, которые можно получить, умножая исходное число на любое целое число.
Свойства кратных чисел
Кратные числа обладают несколькими важными свойствами:
| Сумма кратных чисел | Если два числа являются кратными одному и тому же числу, то их сумма также будет кратна этому числу. Например, если 6 и 9 являются кратными числу 3, то их сумма 15 будет также кратна 3. |
| Произведение кратных чисел | Если два числа являются кратными одному и тому же числу, то их произведение также будет кратно этому числу. Например, если 4 и 7 являются кратными числу 2, то их произведение 28 будет также кратно 2. |
| Деление на кратное число | Если число делится на другое число без остатка, то оно является кратным этому числу. Например, если число 15 делится на число 3 без остатка, то оно является кратным 3. |
| Отношение кратных чисел | Если число A является кратным числу B, то число B является делителем числа A. Например, если число 12 является кратным числу 3, то число 3 является делителем числа 12. |
Знание свойств кратных чисел позволяет решать различные задачи в математике, такие как поиск наименьшего общего кратного или проверка делимости чисел.
Кратность чисел в арифметических операциях
Кратность чисел играет важную роль в арифметических операциях, таких как сложение, вычитание, умножение и деление. Кратность числа показывает, сколько раз это число полностью содержится в другом числе без остатка.
Например, если число 3 является кратным числа 6, это означает, что 6 можно разделить на 3 без остатка. В результате получится целое число 2.
Кратность чисел имеет применение не только в простых математических операциях, но и в различных областях, например в теории чисел, алгебре и физике. Она помогает решать различные задачи, связанные с вычислениями и моделированием.
В арифметических операциях кратность чисел используется для определения, сколько раз нужно повторить операцию сложения, вычитания, умножения или деления, чтобы получить нужный результат.
Например, при умножении числа на 3, его кратность играет роль множителя, который определяет, сколько раз нужно складывать число с самим собой.
Кратность чисел также может быть отрицательной. В этом случае она показывает, сколько раз нужно инвертировать знак числа, чтобы получить нужный результат.
В заключение, кратность чисел является важным понятием в арифметических операциях. Она помогает определить, сколько раз нужно повторить операцию, чтобы получить нужный результат. Понимание кратности чисел поможет в решении различных задач и углубит знание математики.
Видео по теме:
Вопрос-ответ:
Что такое кратное в математике?
В математике, кратным называется число, которое делится на другое число без остатка.
Как узнать, что число является кратным другого числа?
Чтобы узнать, что число является кратным другого числа, необходимо проверить, делится ли оно на это число без остатка. Если делится, то число является кратным, если есть остаток, то число не является кратным.
Чему равно кратное числа?
Кратное числа может быть любым числом, кратным данному числу. Например, кратным числа 3 является 6, 9, 12 и так далее.
Как вычислить кратное числа?
Для вычисления кратного числа необходимо умножить это число на любое целое число. Например, чтобы найти кратное числа 5, можно умножить 5 на 2 и получить 10, на 3 и получить 15 и так далее.
Кратное число и делители

Например, число 10 является кратным числу 5, так как оно делится на 5 без остатка. Другими словами, 10 можно представить в виде произведения 5 и 2: 10 = 5 * 2.
Делитель — это число, на которое делится другое число без остатка. Другими словами, делитель является одним из множителей при разложении числа на простые множители.
Например, для числа 10, делителями являются числа 1, 2, 5 и 10. Число 1 является делителем любого числа, а числа 2, 5 и 10 являются делителями числа 10.
Таким образом, кратное число имеет бесконечное множество делителей, так как оно делится на каждое из чисел в наборе натуральных чисел.
Зная эти определения, мы можем использовать понятие кратного числа и делителей для решения различных задач в математике и других областях.
Применение кратных чисел в реальной жизни
Кратные числа широко применяются в реальной жизни для решения различных задач и удобства в повседневной деятельности. Некоторые из примеров их использования включают:
ПримерОписание
| Календарь | В календаре мы видим, что год состоит из 12 месяцев. Это значит, что количество месяцев в году кратно числу 12. Также, каждый месяц состоит из недель, и количество недель в месяце также кратно числу 4 или 5. |
| Время | Время может быть разделено на часы, минуты и секунды. Каждая минута состоит из 60 секунд, и каждый час состоит из 60 минут. Такое разделение времени на равные кратные единицы упрощает измерение и управление временем в нашей повседневной жизни. |
| Торговля | В торговле кратные числа используются для удобства подсчета и упаковки товаров. Например, товар может быть упакован в коробки, содержащие определенное количество единиц товара, которое является кратным числу 10 или 12. Это упрощает подсчет товаров и определение количества необходимых коробок. |
| Финансы | В финансовой сфере кратные числа используются для удобства подсчета и управления деньгами. Например, многие валюты имеют банкноты и монеты, которые имеют номиналы, кратные определенному числу. Это упрощает обмен деньгами и совершение платежей. |
Применение кратных чисел в реальной жизни помогает упростить многие аспекты нашего повседневного функционирования и повысить эффективность наших действий.


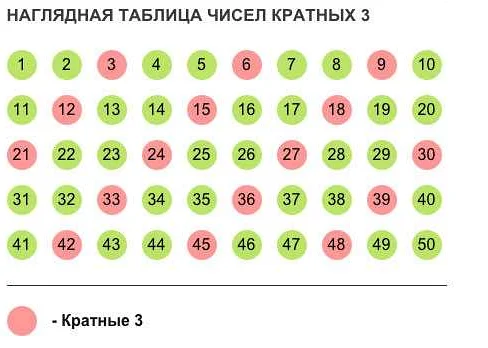

Очень интересная статья! Я всегда задавалась вопросом, что такое кратное в математике. Теперь, благодаря вашей статье, я разобралась в этом вопросе. Кратное это число, которое делится на другое число без остатка. Например, если число 12 делится на 3 без остатка, то 12 — это кратное числа 3. Это очень полезное понятие, особенно когда мы решаем задачи в математике. Теперь я понимаю, что если нам нужно найти все числа, кратные, например, 5, то мы должны просто умножить 5 на любое число. Спасибо за такое простое объяснение! Теперь я точно буду лучше разбираться в математике. С нетерпением жду новых статей!