Что такое луч в математике 3
Содержимое
- 1 Что такое луч в математике 3
- 1.1 Луч в математике: общее определение
- 1.2 Основные свойства луча
- 1.3 Определение и свойства положительного луча
- 1.4 Определение и свойства отрицательного луча
- 1.5 Примеры использования луча в геометрии
- 1.6 Видео по теме:
- 1.7 Вопрос-ответ:
- 1.8 Примеры использования луча в физике
- 1.9 Примеры использования луча в оптике
Луч в математике 3 — это часть прямой, начало которой задано и направление которой ограничено. Узнайте, как определить луч и используйте его свойства в решении задач и геометрических конструкций.
Луч — одно из основных понятий в математике, которое активно применяется в геометрии и аналитической геометрии. Луч представляет собой часть прямой, которая имеет начальную точку и бесконечно продолжается в определенном направлении. Это геометрическое понятие играет важную роль в решении геометрических задач и построении различных геометрических фигур.
Определение луча в математике может быть сформулировано следующим образом: луч — это множество точек, которые расположены на одной прямой и находятся с одной стороны от начальной точки. Луч можно обозначать с помощью двух букв, где первая буква указывает на начальную точку, а вторая — на направление, в котором луч продолжается бесконечно.
Пример использования луча в геометрии: при построении треугольника можно использовать лучи, чтобы определить точку пересечения высот треугольника. В этом случае лучи, исходящие из вершины треугольника и проходящие через основания высот, пересекаются в одной точке — точке пересечения высот.
Лучи также имеют свои свойства, которые позволяют использовать их в различных математических задачах. Например, лучи могут быть параллельными, пересекающимися или наклонными. Знание данных свойств позволяет более точно работать с лучами и использовать их для решения сложных геометрических задач.
Луч в математике: общее определение
Лучом в математике называется часть прямой линии, имеющая начальную точку и располагающаяся в одном направлении. Начальная точка луча называется его началом, а направление, в котором луч располагается, определяется двумя факторами: углом наклона луча и стороной, по которую луч продолжается до бесконечности.
Луч обозначается обычно двумя буквами, одна из которых является начальной буквой слова, обозначающего начало луча, а другая буква является индексом и указывает направление расположения луча. Например, луч, начинающийся в точке А и направленный вправо, может быть обозначен как АВ.
Важным свойством луча является то, что он бесконечно продолжается в направлении, указанном индексом. Это означает, что любая точка, лежащая на луче, будет бесконечно удалена от его начала.
Лучи широко используются в математике для описания направления движения, изображения геометрических фигур и решения различных задач. Они также играют важную роль в геометрии, где служат основой для определения углов и прямых.
ОбозначениеОписание
| АВ | Луч, начинающийся в точке А и направленный вправо |
| CD | Луч, начинающийся в точке С и направленный влево |
| ЕF | Луч, начинающийся в точке Е и направленный вверх |
| GH | Луч, начинающийся в точке G и направленный вниз |
Основные свойства луча

Основные свойства луча:
1. Начальная точка: каждый луч имеет точку, с которой он начинается. Эта точка называется начальной точкой луча.
2. Направление: луч продолжается в бесконечность только в одном направлении. Он не имеет конечной точки.
3. Длина: луч является бесконечным отрезком прямой, поэтому не имеет определенной длины.
4. Название: луч обычно обозначается двумя точками, одна из которых является начальной точкой. Например, луч, начинающийся в точке A и направленный вправо, может быть обозначен как луч AB.
5. Угол: луч может быть использован для измерения углов. Начальная точка луча служит вершиной угла, а сам луч определяет одну из сторон угла.
6. Параллельность: два луча считаются параллельными, если они имеют одинаковое направление или расположены на одной прямой.
7. Пересечение: два луча могут пересекаться в точке, если они имеют общую начальную точку и не параллельны друг другу.
Лучи широко используются в геометрии, физике и других областях математики для описания направлений, углов и линейных отрезков.
Определение и свойства положительного луча
Положительный луч — это луч, который простирается в положительном направлении оси. То есть положительный луч начинается в точке начала и простирается вправо до бесконечности.
Свойства положительного луча:
- Начало положительного луча является точкой, от которой луч начинается.
- Положительный луч простирается вправо и не имеет конечной точки.
- Любая точка на положительном луче имеет большую координату, чем точка начала.
- Положительный луч и отрицательный луч образуют ось, которая делит прямую на две половины.
Примеры использования положительного луча:
- В геометрии положительный луч может использоваться для указания направления движения или расположения объектов.
- В физике положительный луч может представлять направление движения энергии или света.
- В алгебре положительный луч может использоваться для обозначения положительных чисел.
Определение и свойства отрицательного луча
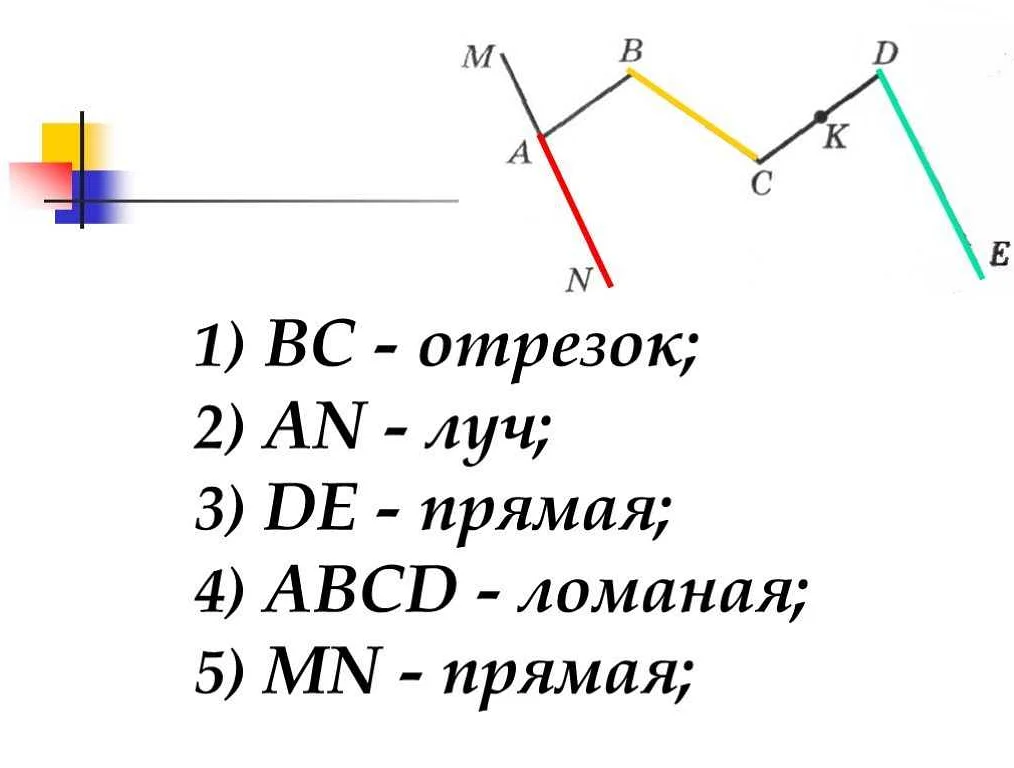
Основным свойством отрицательного луча является то, что он имеет бесконечную длину. Отрицательный луч может продолжать свое распространение вправо или влево на протяжении всей числовой оси.
Отрицательный луч также обладает свойством, что все точки на нем расположены слева от начальной точки. То есть, если задана начальная точка A, то все точки отрицательного луча будут находиться левее A на числовой оси.
Отрицательные лучи широко используются в математике, физике и других науках для описания направления движения или представления отрицательных значений на числовой оси.
Примеры использования луча в геометрии
Вот несколько примеров использования луча в геометрии:
- Определение угла. Луч может использоваться для определения угла. Для этого необходимо провести два луча с общей начальной точкой и измерить величину угла между ними.
- Построение биссектрисы угла. Луч может быть использован для построения биссектрисы угла, то есть прямой, которая делит данный угол пополам. Для этого необходимо провести два луча, образующих данный угол, и провести луч, проходящий через его вершину и делящий его пополам.
- Построение отрезка с заданной длиной. Луч может быть использован для построения отрезка с заданной длиной. Для этого необходимо определить точку на луче, удаленную от начальной точки на нужное расстояние, и провести отрезок, соединяющий начальную точку и найденную точку.
- Определение местоположения точки относительно луча. Луч может быть использован для определения местоположения точки относительно него. Если точка находится на луче, то она лежит на нем. Если точка находится слева от луча, то она находится в его отрицательной полуплоскости. Если точка находится справа от луча, то она находится в его положительной полуплоскости.
Это лишь некоторые из множества примеров использования луча в геометрии. Луч является важным элементом для решения различных геометрических задач и имеет множество применений в практике.
Видео по теме:
Вопрос-ответ:
Что такое луч в математике?
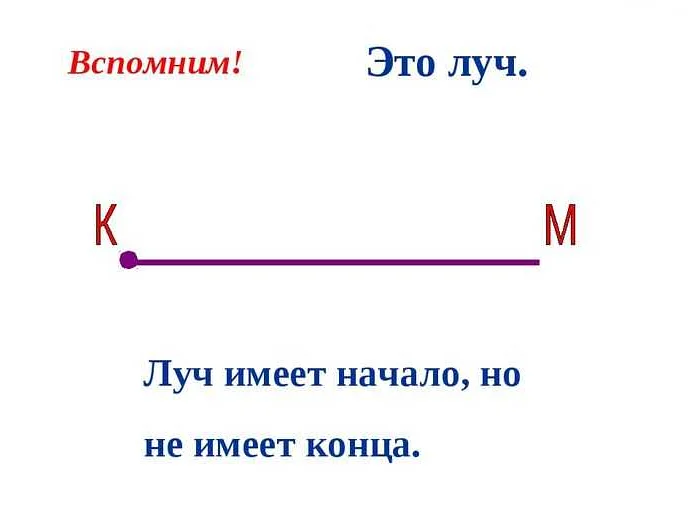
Луч в математике — это часть прямой линии, которая имеет начало в определенной точке и продолжается бесконечно в одном направлении.
Какими свойствами обладает луч в математике?
Луч имеет два важных свойства: он имеет начальную точку и продолжается бесконечно в одном направлении. Также луч можно продлить в обратном направлении, но это уже будет другой луч с другой начальной точкой.
Как можно использовать лучи в математике?
Лучи могут использоваться для задания направления движения или ориентации в пространстве. Они также широко применяются в геометрии для построения углов, отрезков и других фигур.
Можно ли измерить длину луча в математике?
Нет, нельзя измерить длину луча, так как он продолжается бесконечно в одном направлении. Длина луча неопределена и неизмерима.
Примеры использования луча в физике
Лучи широко используются в физике для описания и изучения различных явлений и процессов.
Преломление лучей света. Лучи света, падающие на границу раздела двух сред с различными оптическими свойствами, могут изменять свое направление при переходе из одной среды в другую. Это явление называется преломлением. Направление преломленного луча определяется законом преломления, который связывает углы падения и преломления с показателями преломления сред. Использование лучей позволяет описать и предсказать, как будет преломлен свет при прохождении через линзы, призмы, стекло и другие оптические элементы.
Пример: При падении светового луча на поверхность плоского стекла под углом, большим критического угла, происходит полное отражение луча. Это явление называется полным внутренним отражением. Используя лучи, можно показать, как изменяется направление отраженного луча при изменении угла падения.
Излучение и поглощение электромагнитных волн. Лучи также используются для описания излучения и поглощения электромагнитных волн, таких как радиоволны, световые лучи, рентгеновские лучи и другие. Излучение и поглощение волн связаны с энергетическими и частотными характеристиками этих волн. Лучи позволяют визуализировать и анализировать распространение электромагнитных волн в пространстве и взаимодействие волн с различными объектами.
Пример: Лучи рентгеновских лучей используются в медицине для получения изображений внутренних органов и тканей. При прохождении через тело, рентгеновские лучи поглощаются различными структурами, такими как кости и органы, что позволяет получить диагностическую информацию о состоянии организма.
Распространение звуковых волн. Звуковые волны также могут быть описаны с помощью лучей. Лучи звука позволяют изучать направление распространения звука и его взаимодействие с различными объектами и средами. Лучи звука позволяют моделировать и анализировать рассеяние, отражение и преломление звуковых волн.
Пример: Лучи звука используются в ультразвуковых устройствах для создания изображений внутренних органов. При прохождении через ткани и органы, ультразвуковые волны отражаются от границ различных структур, и эхо отраженных волн используется для получения диагностической информации.
Примеры использования луча в оптике
Лучи в оптике используются для описания пути, по которому свет распространяется. Они играют важную роль в понимании оптических явлений и применяются в различных областях оптики.
1. Преломление света. Лучи используются для объяснения преломления света при переходе из одной среды в другую. В соответствии с законом преломления, лучи света меняют направление при переходе через границу раздела сред, а углы отклонения зависят от показателей преломления сред.
2. Формирование изображений. Лучи также помогают объяснить, как формируются изображения в оптических системах, таких как линзы и зеркала. При прохождении через линзу, лучи света могут собираться или рассеиваться, создавая увеличенное или уменьшенное изображение предмета.
3. Дифракция света. Лучи применяются для описания явления дифракции света, которое происходит, когда свет проходит через узкое отверстие или препятствие. Дифракция приводит к изменению формы лучей и созданию интерференционных полос или рассеянию света.
4. Рассеяние света. Лучи также используются для объяснения явления рассеяния света, которое происходит, когда свет взаимодействует с маленькими частицами в среде. Рассеяние света может привести к образованию различных эффектов, таких как радуга или синее небо.
Лучи в оптике играют важную роль в понимании и объяснении оптических явлений и применяются в различных областях, таких как медицина, фотография и проекционные системы.


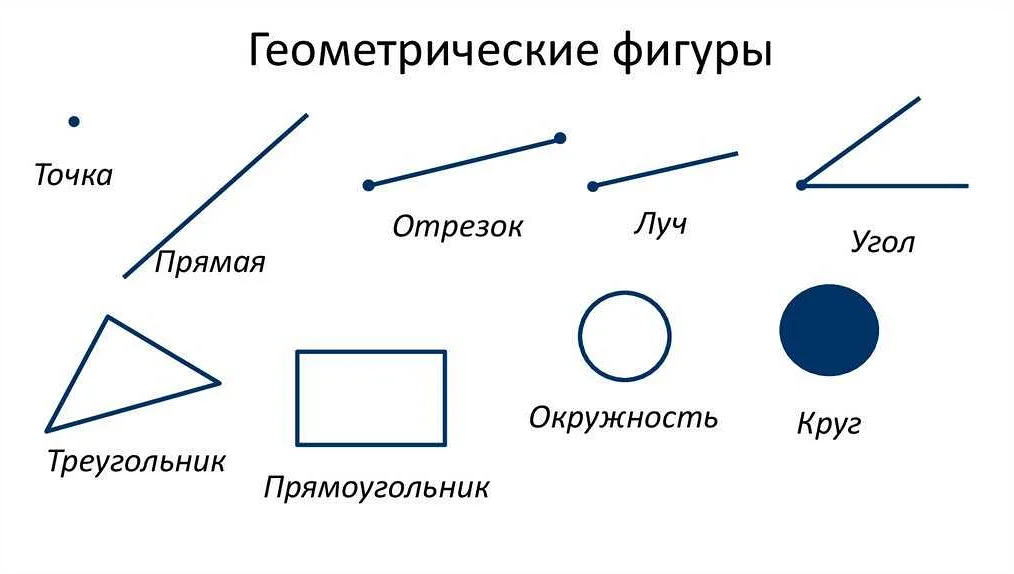
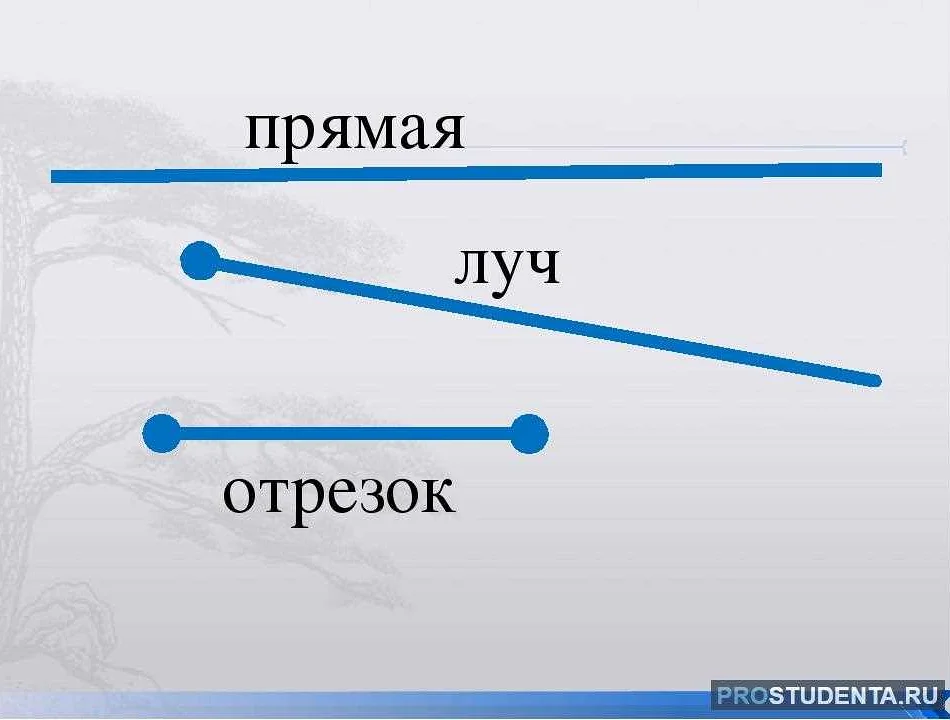
Статья очень интересная и понятная для меня, как для неспециалиста в математике. Я узнала, что луч — это часть прямой, которая имеет начало в определенной точке и простирается бесконечно в одном направлении. Мне понравилось, что автор объяснил не только определение луча, но и его свойства. Теперь я знаю, что луч имеет только одно начало, но не имеет конца, и он бесконечен в одном направлении. Примеры использования лучей в реальной жизни, такие как использование их в геометрии, физике и оптике, помогли мне лучше понять, как они применяются на практике. Статья была написана простым и понятным языком, что позволило мне легко усвоить информацию. Очень приятно, что математика может быть доступной и интересной даже для неспециалистов.