Луч что это такое по математике

Луч в математике — это прямая линия, которая распространяется бесконечно в одном направлении. Узнайте, как определить луч, его свойства и применение в геометрии.

Луч — одно из основных понятий геометрии, которое широко используется в математике. Луч — это отрезок прямой, который начинается в определенной точке и распространяется бесконечно далеко в одном направлении. Он имеет только одну начальную точку, которая называется началом луча.

Луч можно представить как стрелку, которая указывает на бесконечность. Начало луча указывается точкой, а направление луча обозначается стрелкой. Луч является открытым множеством, то есть он содержит все точки, лежащие на прямой, начиная с начальной точки и продолжая бесконечно в одну сторону.

Луч широко используется в математике для описания направления движения объектов, прямых линий, углов и других геометрических фигур. Он также является важным инструментом для решения различных задач по геометрии и алгебре.

Запомните, что луч — это бесконечно длинный отрезок прямой, который начинается в определенной точке и распространяется бесконечно далеко в одном направлении.

Значение и свойства луча в математике

Луч в математике представляет собой особую геометрическую фигуру, которая имеет начальную точку и протяженность в одном направлении. Начальная точка называется началом луча, а направление указывается стрелкой или указателем. Луч может быть ограниченным или бесконечным.

Одно из основных свойств луча — его направление. Луч может быть направлен вправо, влево, вверх или вниз. В зависимости от направления луча, его можно классифицировать как положительный или отрицательный.

Другое свойство луча — его протяженность. Луч может быть конечным, то есть иметь определенную длину, или бесконечным, то есть не иметь конца.

Луч можно представить в виде линейного графика на координатной плоскости. Начало луча будет соответствовать точке (0, 0), а направление будет указывать, в какую сторону двигаться на плоскости.

Луч также может использоваться для определения угла. Например, два луча с общим началом могут образовывать угол, который измеряется в градусах или радианах.

В итоге, луч в математике является важной геометрической фигурой, которая имеет свои уникальные свойства и может быть использована для моделирования различных математических концепций.

Определение луча

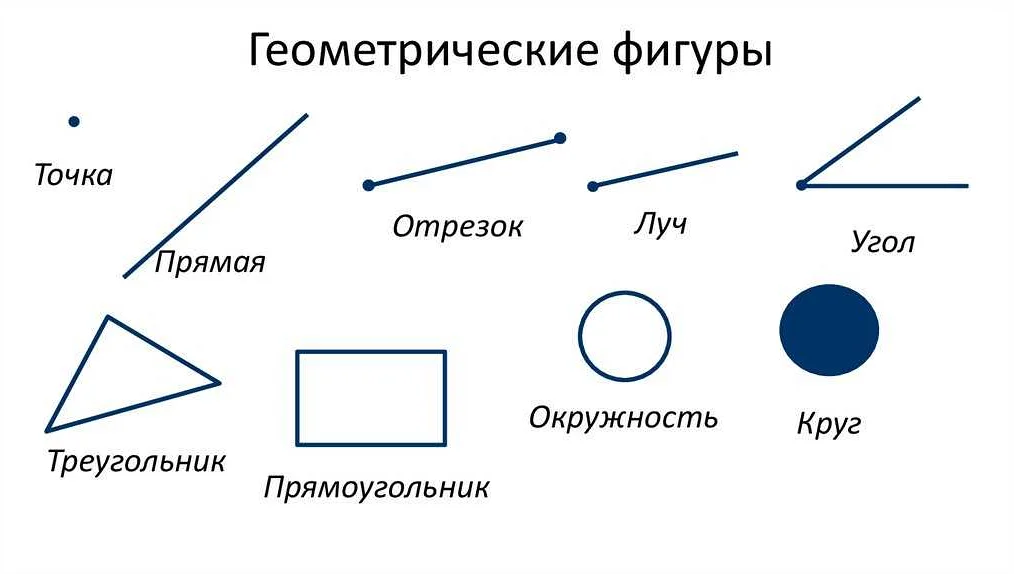
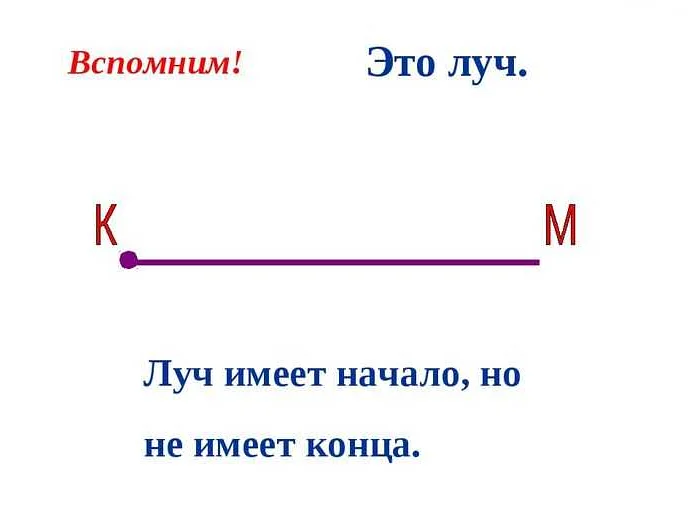
Луч имеет одну точку начала, которая называется началом луча, и она обозначается точкой. Луч не имеет конечной точки, поэтому его длина бесконечна.

Луч можно представить с помощью символа стрелки, которая указывает направление продолжения луча.

Лучы в математике широко используются для решения геометрических задач и в различных областях науки и техники.

Одномерность луча

Луч имеет следующие свойства:

СвойствоОписание

Направление	Луч имеет определенное направление от начальной точки в бесконечность.
Бесконечность	Луч не имеет конечной длины и продолжается в бесконечность.
Начало	Луч определяется начальной точкой, которая является его началом.
Единственность	Луч определен однозначно по своей начальной точке и направлению.

Луч может быть направлен вправо, влево или вертикально вверх или вниз. В зависимости от направления луча, его можно классифицировать как положительный (вправо или вверх) или отрицательный (влево или вниз).

Луч встречается в различных областях математики, физики и геометрии и используется для моделирования прямых линий, векторов и радиационных лучей.

Направление луча

Луч в математике представляет собой прямую линию, которая начинается в определенной точке и продолжается в бесконечность. Когда говорят о направлении луча, имеется в виду движение вдоль этой линии.

Направление луча может быть задано двумя способами:

НаправлениеОписание

Прямое направление	Луч распространяется от начальной точки в положительном направлении прямой линии.
Обратное направление	Луч распространяется от начальной точки в отрицательном направлении прямой линии.

Направление луча важно при решении математических задач, таких как определение пересечений лучей или вычисление углов между лучами. Оно также может быть использовано для задания ориентации в пространстве.

Бесконечность луча

Бесконечность луча означает, что луч продолжается в бесконечность в одном направлении. Это означает, что даже если мы продолжим двигаться по лучу, мы никогда не достигнем его конца. Бесконечность луча показывает отсутствие конечности и неограниченность луча.

В математике бесконечность луча обозначается символом ∞ (бесконечность), который помещается на конце луча, указывая на его бесконечное продолжение.

Бесконечность луча имеет несколько интересных свойств. Например, луч можно продлить до бесконечности в обоих направлениях. Кроме того, любая точка на луче бесконечности лежит бесконечно далеко от начальной точки луча.

Бесконечность луча широко используется в математике и физике, особенно в анализе и геометрии. Она позволяет рассматривать и изучать бесконечные множества и функции, а также моделировать некоторые физические процессы, которые имеют бесконечное продолжение.

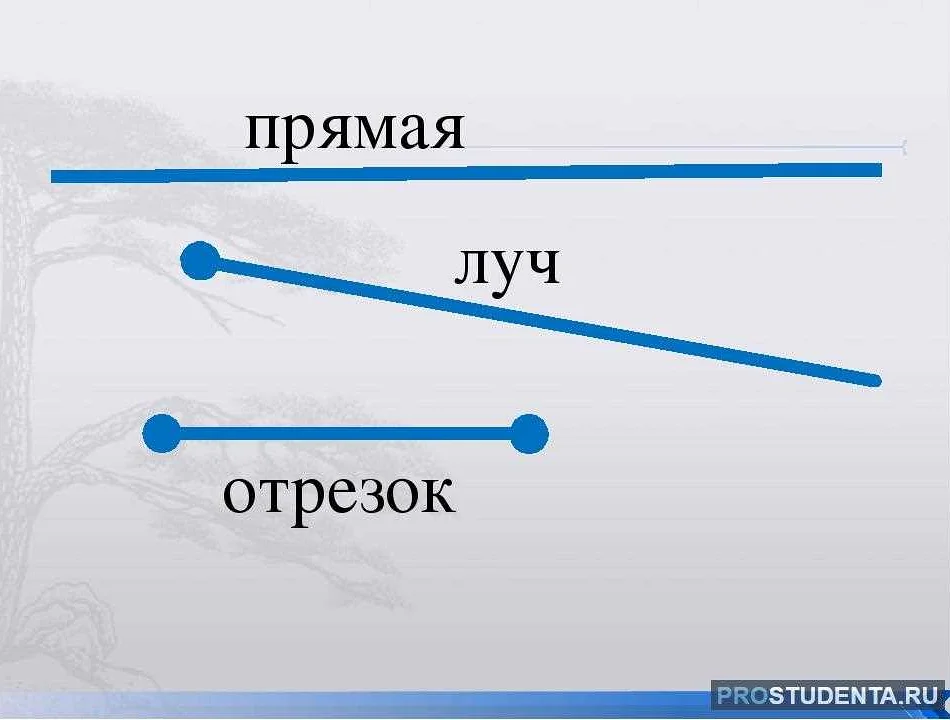
Отличие луча от отрезка

ПризнакЛучОтрезок

Определение	Луч — это множество всех точек, лежащих на прямой и расположенных по одну сторону от начальной точки.	Отрезок — это множество всех точек, лежащих на прямой и находящихся между двумя заданными точками начала и конца отрезка.
Направление	Луч имеет определенное направление от начальной точки.	Отрезок не имеет определенного направления.
Бесконечность	Луч продолжается до бесконечности в указанном направлении.	Отрезок имеет конечную длину и не расширяется до бесконечности.

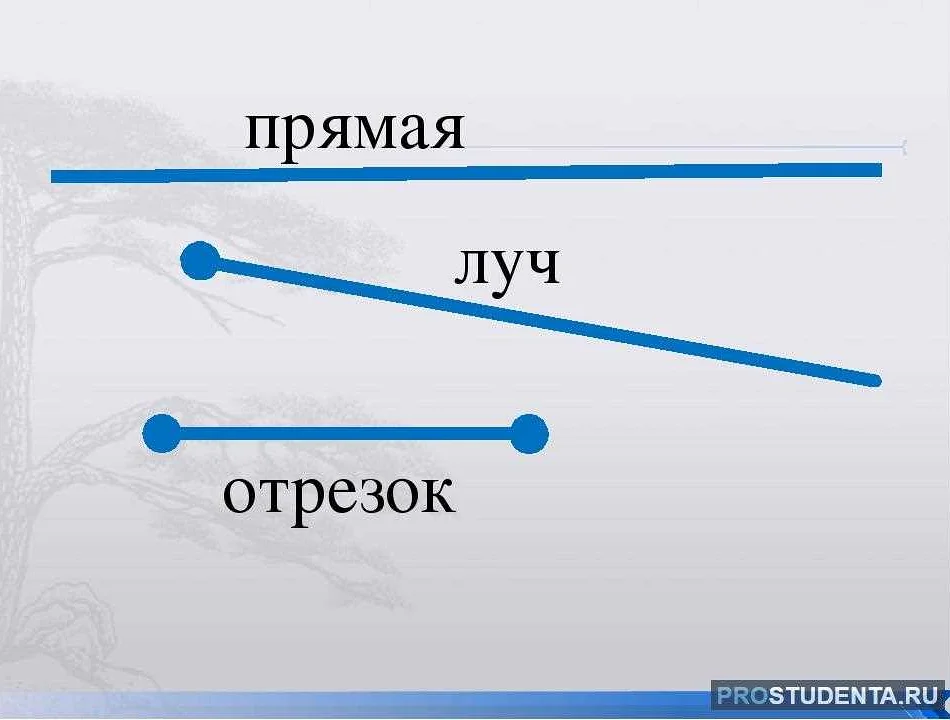
Таким образом, основное отличие луча от отрезка заключается в их определении, направлении и бесконечности. Луч распространяется в одном направлении от начальной точки и продолжается до бесконечности, в то время как отрезок имеет конечную длину и не имеет определенного направления.

Геометрическое представление луча

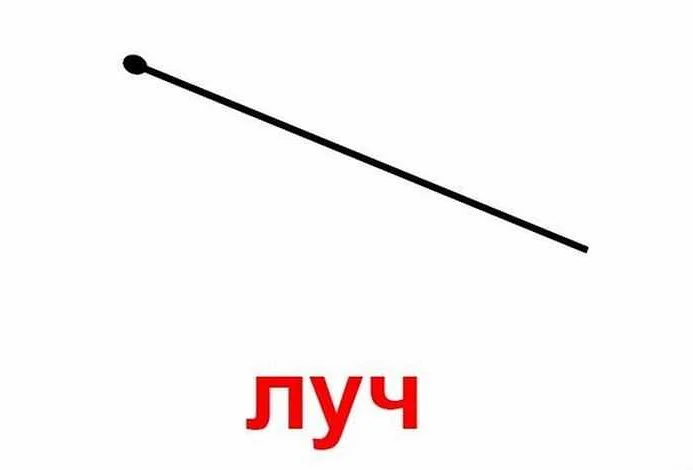
Луч в геометрии представляет собой отрезок, имеющий начальную точку и направление. Начальная точка называется началом луча, а направление определяет бесконечно дальнюю точку, которая лежит на прямой и проходит через начальную точку.

Геометрический луч может быть представлен на координатной плоскости или в трехмерном пространстве. На плоскости луч обозначается стрелкой, указывающей на направление. Начало луча представляется точкой, от которой исходит стрелка.

Луч может быть ограниченным или неограниченным. Ограниченный луч имеет конечную длину и заканчивается в некоторой точке. Неограниченный луч имеет бесконечную длину и не имеет конечной точки.

Геометрическое представление луча является важным инструментом в решении различных задач и проблем. Лучи используются в геометрии, оптике, физике, компьютерной графике и других областях науки и техники.

Применение лучей в математике

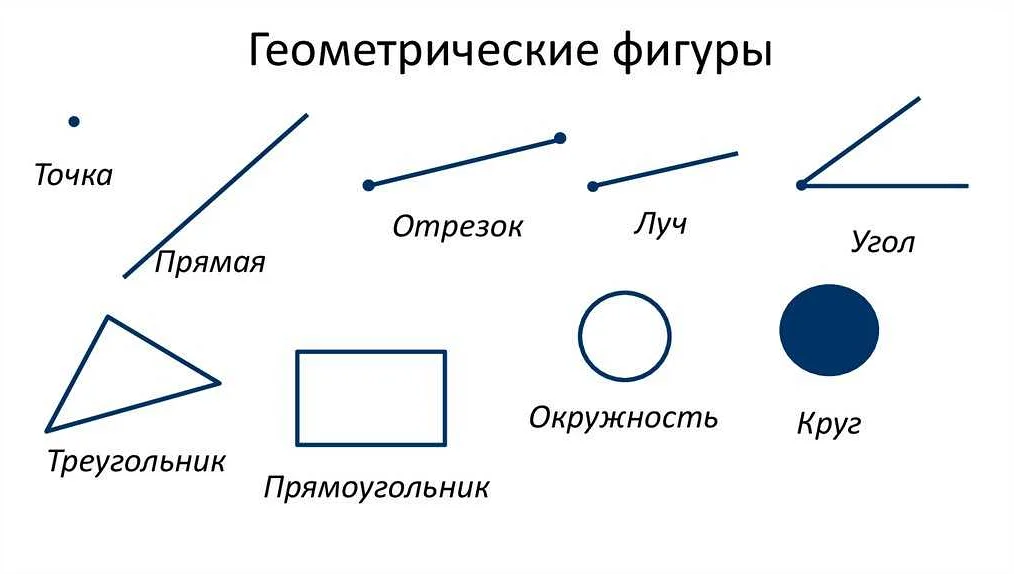
Одно из основных применений лучей — это построение геометрических фигур и определение их свойств. С помощью лучей мы можем определить углы, их величину и положение, а также проводить прямые и перпендикулярные линии.

Лучи также применяются для решения задач на геометрическую оптику. Например, они помогают нам понять, как свет распространяется и отражается от поверхностей. Мы можем использовать лучи, чтобы определить путь света и предсказать его поведение.

В физике лучи используются для изучения процессов распространения энергии и взаимодействия среды с внешними объектами. Они позволяют нам моделировать и анализировать различные физические явления, например, распространение звука и электромагнитные волны.

Лучи также широко применяются в оптимизации и математическом моделировании. Они помогают нам находить оптимальные решения в различных задачах, например, в задачах линейного программирования или поиске оптимального пути.

Таким образом, лучи играют важную роль в математике и науке в целом. Они помогают нам лучше понять и изучать окружающий мир, а также решать сложные задачи и строить точные модели.

Взаимное расположение лучей

При изучении лучей в математике важно понимать их взаимное расположение. Лучи могут быть расположены следующими способами:

• Пересекающиеся лучи: два луча пересекаются в одной точке.
• Совпадающие лучи: два луча имеют одну и ту же начальную точку и направление.
• Параллельные лучи: два луча имеют одинаковое направление, но не пересекаются.
• Перпендикулярные лучи: два луча пересекаются под прямым углом.

Знание взаимного расположения лучей позволяет решать различные задачи, связанные с геометрией, оптикой и другими областями науки и техники.

Например, в оптике знание взаимного расположения лучей позволяет определить, будет ли свет преломляться или отражаться от поверхности, а также каким образом будет меняться направление световых лучей при прохождении через линзы или призмы.

Видео по теме:

Как определить луч в математике?

Луч — это часть прямой, ограниченная двумя точками, одна из которых называется началом луча, а другая — направляющей точкой.

Можно ли измерить длину луча?

Нет, луч не имеет конечной длины, поэтому его нельзя измерить.

Как лучи используются в геометрии?

Лучи используются в геометрии для задания направления и определения относительного положения прямых, отрезков и других геометрических фигур.

Что такое луч в математике?

Луч в математике — это геометрическая фигура, которая представляет собой прямую линию, начинающуюся в одной точке и не имеющую конца. Луч имеет только направление и бесконечную протяженность в этом направлении.