С чего начинается математический луч

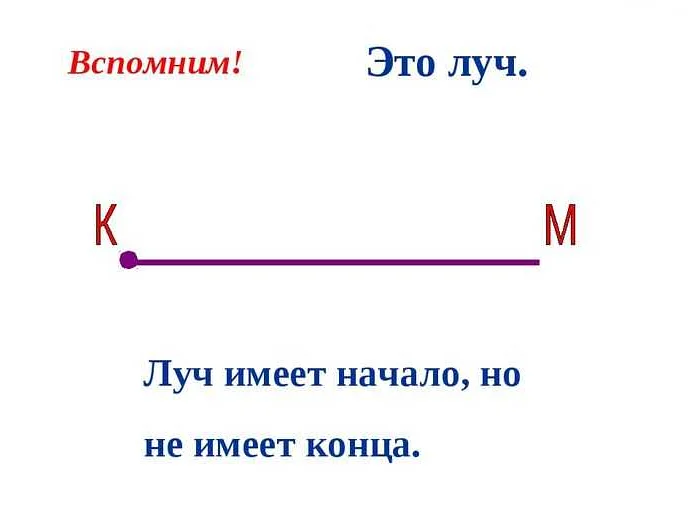
Математический луч – это основной элемент геометрической фигуры, который начинается с определенной точки и простирается в бесконечность в одном направлении. Узнайте, как определить начальную точку и направление математического луча и как он используется в различных математических задачах и теориях.

Математика — это наука, изучающая количество, структуру, пространство и изменение. Она имеет свои основные понятия и принципы, которые служат фундаментом для всех ее ветвей. Одним из таких понятий является математический луч.

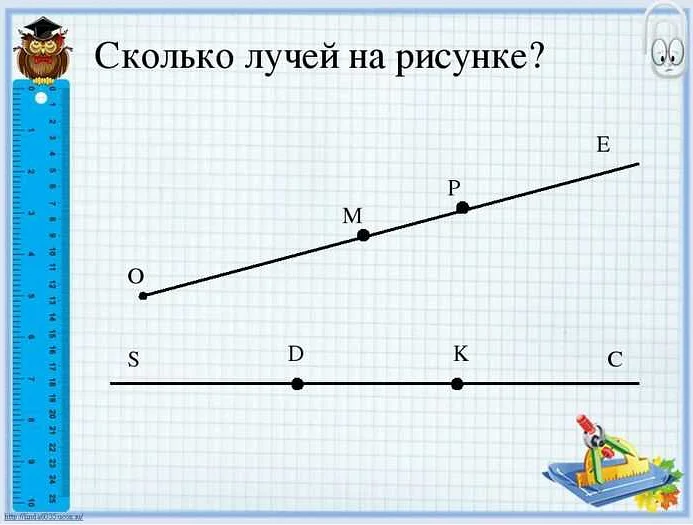
Математический луч — это прямая линия, у которой есть начало (или начальная точка) и простирается в определенном направлении бесконечно далеко. Он может быть направлен вправо или влево от начальной точки, и обозначается обычно двумя буквами, например, AB или CD.

У математического луча есть несколько основных свойств. Во-первых, он имеет только одно начало, то есть только одну точку, из которой он исходит. Во-вторых, он состоит из всех точек, которые находятся на его линии и находятся с одной стороны от начальной точки. Таким образом, все точки на линии лежат либо слева, либо справа от начальной точки.

Математический луч часто используется в геометрии и алгебре для описания направления и положения объектов. Он помогает определить относительную длину и положение отрезков, углов, а также решать уравнения и неравенства. Понимание основных понятий и принципов математического луча является важным шагом при изучении математики и позволяет решать разнообразные задачи в различных областях знания.

История и развитие математического луча

Первоначально математический луч рассматривался как геометрический объект, не имеющий физического эквивалента. Он был представлен как прямая линия, идущая в бесконечность, начинающаяся в точке и не имеющая конца. Такое представление луча использовалось для решения геометрических задач и построения геометрических фигур.

С течением времени понятие математического луча стало развиваться и приобрело новые аспекты. В математическом анализе луч используется для описания направления функции и множества точек с определенными свойствами. Также луч используется в физике для описания движения света и других физических явлений.

Современная математика и физика широко используют понятие математического луча для анализа и решения различных задач. История и развитие математического луча отражает не только эволюцию математической науки, но и ее связь с другими областями знания, такими как физика и информатика.

Роль математического луча в различных областях науки и техники

В физике математический луч позволяет описывать и понимать физические явления. С его помощью можно предсказывать движение объектов, описывать электромагнитные поля, анализировать взаимодействие частиц и многое другое. Без математического луча не было бы возможности формулировать точные законы физики и проводить сложные вычисления.

В области экономики и финансов математический луч используется для анализа и прогнозирования различных финансовых процессов. Он позволяет моделировать экономические системы, определять оптимальные стратегии инвестирования и риски. Благодаря математическому лучу можно проводить сложные расчеты для определения цен на товары и услуги, анализировать рыночную конъюнктуру и принимать решения на основе математических моделей.

В технике математический луч используется для проектирования и оптимизации различных механизмов и систем. Он помогает инженерам решать задачи связанные с прочностью конструкций, оптимальным распределением ресурсов, эффективностью рабочих процессов и т.д. Математический луч позволяет проводить сложные расчеты и моделирование, что способствует разработке новых технологий и улучшению существующих систем.

Математический луч также находит применение в других областях науки, таких как биология, химия, информатика и т.д. Он помогает анализировать и интерпретировать полученные данные, строить модели и прогнозировать результаты экспериментов.

Таким образом, математический луч играет важную роль в различных областях науки и техники, обеспечивая точность и надежность в решении сложных задач и моделировании реальных систем.

Основные понятия и определения, связанные с математическим лучом

Начало луча обозначается точкой и обычно обозначается буквой A, B, C и т.д., а сам луч обозначается двумя точками, например, AB.

Математический луч может быть направлен вправо или влево. Если луч направлен вправо, то его можно обозначить как луч AB, а если луч направлен влево, то он может быть обозначен как луч BA.

Математический луч также может быть бесконечным или конечным. Если луч имеет конечную длину, то он называется конечным. Если же луч не имеет конечной длины и продолжается в бесконечность, он называется бесконечным лучом.

В математическом луче можно выделить следующие основные понятия и определения:

ТерминОпределение

Начало луча	Точка, от которой начинается математический луч.
Направление луча	Направление, в котором простирается математический луч.
Бесконечный луч	Луч, который не имеет конечной длины и продолжается в бесконечность.
Конечный луч	Луч, который имеет конечную длину.

Свойства и характеристики математического луча

Основные свойства и характеристики математического луча:

1. Начальная точка: Математический луч начинается с определенной точки, которая называется начальной точкой. Вся прямая, на которой лежит луч, расположена с одной стороны от этой точки.

2. Направление: Математический луч простирается бесконечно в одном направлении от начальной точки. Направление луча указывается стрелкой, которая указывает, в каком направлении он продолжается.

3. Бесконечность: Математический луч не имеет конечной длины и простирается бесконечно в одном направлении. Он не имеет конечной точки и не ограничен.

4. Угол: Математический луч может быть использован для измерения угла. Он может быть использован как начальная сторона для построения угла, где его начальная точка служит вершиной угла.

5. Параллельность: Два математических луча могут быть параллельными, если они расположены на одной прямой и направлены в одном и том же направлении.

Математический луч является важным понятием в геометрии и имеет множество применений в различных математических задачах и теориях.

Виды и классификации математических лучей

1. Прямой луч:

Прямой луч начинается в заданной точке (начальной точке) и продолжается бесконечно в одном направлении. Он обозначается двумя точками, где первая точка указывает на начальную точку, а вторая — на направление.

2. Обратный луч:

Обратный луч начинается в заданной точке (начальной точке) и продолжается бесконечно в противоположном направлении. Он также обозначается двумя точками, но вторая точка указывает на противоположное направление.

3. Угловой луч:

Угловой луч образуется двумя прямыми лучами, которые имеют общую начальную точку и расходятся в разных направлениях. Этот луч обозначается тремя точками, где первая точка указывает на общую начальную точку, а две другие — на направления расхождения.

Классификация математических лучей позволяет более точно описывать и понимать их свойства и взаимодействия с другими геометрическими фигурами. Знание этих видов и классификаций является основой для изучения более сложных понятий и задач в математике.

Принципы и правила работы с математическим лучом

• Начальная точка: математический луч всегда имеет начальную точку, от которой он начинается. Эта точка играет важную роль, так как определяет направление луча.
• Бесконечное продолжение: математический луч не имеет конечной длины. Он продолжается бесконечно далеко в одном направлении. Это позволяет использовать луч для описания процессов, которые не имеют конечного предела.
• Направление: каждый математический луч имеет свое направление, которое определяется его начальной точкой. Луч может быть направлен влево или вправо, вверх или вниз, но не может менять направление в процессе своего продолжения.

Кроме основных принципов, существуют и другие правила, которые помогают работать с математическим лучом. Некоторые из них включают:

1. Определение положения точки: математический луч может помочь в определении положения точки на числовой прямой. Если точка находится на луче, то можно сказать, что ее координата больше или меньше начальной точки луча.
2. Определение интервала: математический луч может быть использован для определения интервала на числовой прямой. Например, луч может помочь определить все значения, которые находятся между двумя заданными точками.
3. Использование неравенств: математический луч может быть использован для записи неравенств. Например, x > 2 означает, что x находится справа от числа 2 на числовой прямой.

Правила работы с математическим лучом помогают нам лучше понимать и использовать этот математический объект в различных задачах. Знание этих принципов и правил является важным для успешного решения математических задач и применения математических концепций в реальной жизни.

Применение математического луча в решении различных задач

Одной из основных задач, которую можно решить с помощью математического луча, является нахождение корней уравнений. Математический луч позволяет нам визуализировать график уравнения и найти точки пересечения с осью абсцисс. Это важно для определения значений переменных, при которых уравнение равно нулю.

Другим применением математического луча является нахождение экстремумов функций. Математический луч помогает нам определить, где функция достигает своих максимальных или минимальных значений. Это полезно при оптимизации процессов и поиске наилучших решений.

Кроме того, математический луч используется для построения графиков функций и анализа их свойств. Он позволяет нам изучать изменение функций в зависимости от значения аргумента и определять их основные характеристики, такие как возрастание, убывание, перегибы и асимптоты.

Математический луч также применяется в геометрии для решения различных задач, связанных с прямыми и углами. Он позволяет нам находить точки пересечения прямых, определять углы между прямыми и находить расстояния между точками.

В заключение, математический луч является мощным инструментом, который позволяет нам решать различные задачи в математике и других научных областях. Он помогает нам визуализировать и анализировать данные, находить корни уравнений, находить экстремумы функций и проводить геометрические расчеты. Использование математического луча позволяет нам получить более глубокое понимание и развить наши навыки в математике.

Современные технологии и инструменты для работы с математическим лучом

С развитием информационных технологий появилось множество интересных инструментов и технологий, которые помогают работать с математическим лучом более эффективно и удобно.

Одним из таких инструментов являются компьютерные программы для математических расчетов, такие как MATLAB, Mathematica, Maple и другие. Эти программы позволяют выполнять сложные математические вычисления, решать уравнения, проектировать и анализировать системы, проводить численные эксперименты и многое другое.

Также существуют онлайн-сервисы и приложения, которые предоставляют доступ к различным математическим инструментам и ресурсам. Например, Wolfram Alpha — это мощный компьютерный движок, способный решать математические задачи, а также предоставлять детальную информацию о различных математических понятиях и теориях.

Кроме того, современные графические пакеты и инструменты для визуализации данных позволяют создавать красочные и наглядные графики, которые помогают визуализировать математические понятия и результаты исследований. Например, графические пакеты R и Python с библиотекой Matplotlib позволяют создавать разнообразные типы графиков и диаграмм.

Также стоит отметить использование интерактивных математических платформ, таких как GeoGebra. Этот инструмент предоставляет возможность создания интерактивных математических моделей, графиков и геометрических построений. Это позволяет студентам и преподавателям взаимодействовать с математическими объектами, менять параметры и наблюдать изменения в реальном времени.

Современные технологии и инструменты значительно упрощают работу с математическим лучом, делают ее более удобной и эффективной. Они позволяют производить сложные вычисления, визуализировать результаты и взаимодействовать с математическими объектами. Благодаря этому, математический луч становится доступным и интересным для широкого круга людей.

Вопрос-ответ:

Что такое математический луч?

Математический луч — это часть прямой, которая имеет начальную точку и простирается бесконечно в одном направлении. Начальная точка луча называется началом, а направление, в котором луч простирается, называется направлением луча.

Какие основные понятия связаны с математическим лучом?

Основные понятия, связанные с математическим лучом, это начало луча, направление луча, конец луча. Начало луча — это точка, с которой начинается луч. Направление луча — это направление, в котором луч простирается. Конец луча — это точка, до которой простирается луч.

Как определить расположение точки относительно луча?

Для определения расположения точки относительно луча используется понятие положительности и отрицательности. Если точка находится на луче, то расстояние от начала луча до этой точки будет положительным. Если точка находится слева от начала луча, то расстояние от начала луча до этой точки будет отрицательным.

Какие принципы лежат в основе математического луча?

Основным принципом математического луча является то, что он простирается бесконечно в одном направлении. Это означает, что луч не имеет конечной длины и не имеет конечного конца. Еще одним принципом является то, что луч имеет начальную точку, с которой он начинается.

Видео по теме: