Что такое луч в математике

Луч в математике – это бесконечная полупрямая, начало которой задается одной точкой, а направление определяется другой точкой. Узнайте, как использовать лучи в геометрии и алгебре, и как они помогают решать различные задачи.

В математике луч — это одно из основных понятий геометрии, которое используется для описания прямой линии, выходящей из какой-то точки и продолжающейся в одном направлении до бесконечности. Лучи часто используются для моделирования и анализа пространственных объектов и процессов.

Основное определение луча в математике — это множество точек на прямой, начинающееся с определенной точки, называемой началом луча, и продолжающееся в одном направлении. Луч можно представить с помощью стрелки, которая указывает направление продолжения.

Лучи в математике могут быть направлены влево или вправо, вверх или вниз, а также в других направлениях. Луч, направленный вправо, обычно обозначается символом → и называется положительным лучом. Луч, направленный влево, обозначается символом ← и называется отрицательным лучом. Начало луча можно обозначить буквой, например, точка A, а сам луч — буквой и стрелкой, например, луч AB.

Лучи в математике имеют ряд свойств и характеристик, которые позволяют проводить различные операции и вычисления с ними. Например, лучи могут пересекаться, образуя углы, они могут быть параллельными или перпендикулярными друг другу. Кроме того, лучи могут быть использованы для определения прямых, плоскостей и других геометрических фигур и объектов.

Луч как геометрическая фигура

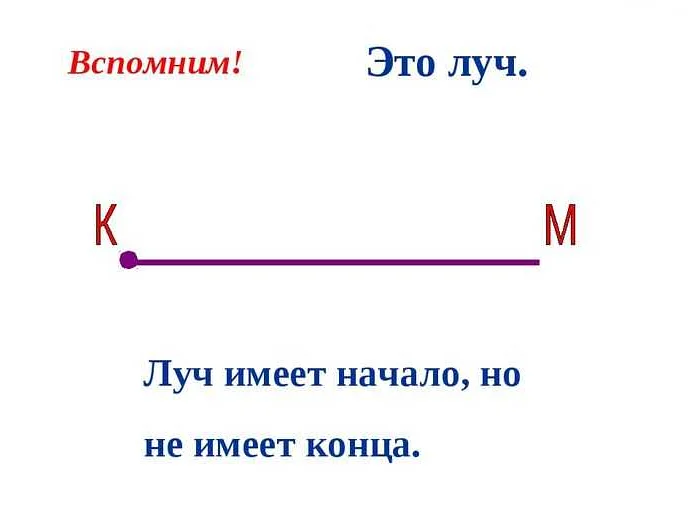
Луч обычно обозначается двумя буквами, например, AB. Точка A называется начальной точкой луча, а направление от точки A до точки B называется направлением луча.

Главное свойство луча заключается в том, что он имеет только одну начальную точку, но простирается бесконечно в одном направлении. Это отличает луч от отрезка, который имеет две конечные точки.

Луч может быть направлен вправо или влево, вверх или вниз, или в любом другом направлении на плоскости. Он может пересекать другие линии или плоскости, образуя углы с ними.

Лучи широко используются в геометрии и физике для описания направления движения, распространения света и других физических явлений.

Определение луча в математике

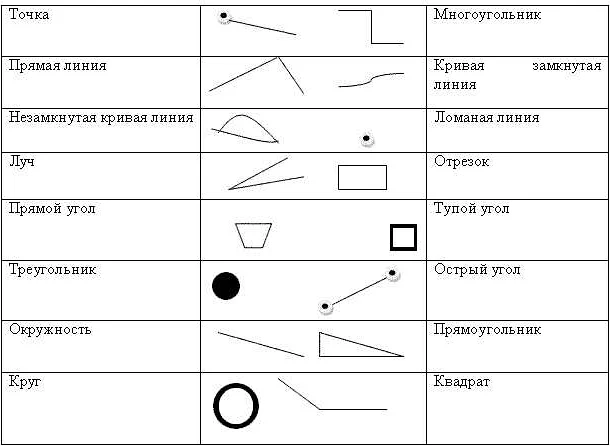
Луч имеет два важных свойства:

1. Луч имеет определенное направление от начальной точки в бесконечность. Точки, лежащие на луче, находятся на одной стороне от начальной точки.
2. Луч не имеет конечной длины и не имеет конечной границы.

Луч может быть направлен как вправо, так и влево. Луч, направленный вправо, называется направленным вправо лучом, а луч, направленный влево, называется направленным влево лучом.

Лучи используются в различных математических и геометрических задачах, таких как определение углов, построение графиков функций и многое другое.

Основные свойства луча

Основные свойства луча:

• Луч не имеет конечной длины, он простирается бесконечно в одном направлении.
• Луч имеет только одно начало, но не имеет конца.
• Луч можно обозначить двумя способами: либо двумя точками, где первая точка — начало луча, а вторая точка — любая другая точка на луче; либо названием начальной точки и одной буквой, например, луч AB.
• Луч можно ориентировать в одном из двух направлений: вправо или влево.

Лучи активно используются в геометрии и физике, помогая решать различные задачи и строить модели.

Луч как часть прямой

В математике лучом называется часть прямой, которая начинается в некоторой точке и продолжается в определенном направлении до бесконечности. Луч имеет только одно начало, называемое его началом, и не имеет конца.

Луч обозначается двумя точками, где первая точка указывает на его начало, а вторая точка на самом луче не находится. Например, если луч обозначен точками A и B, то A — начало луча, а B лежит на прямой, но не на самом луче.

Луч можно представить как бесконечную полупрямую. Он расширяется в одном направлении и не имеет конечной длины.

Луч может быть направлен вправо, влево, вверх или вниз. В зависимости от направления луча он может быть назван соответствующим именем. Например, если луч направлен вправо, он называется правым лучом, если влево — левым лучом, если вверх — верхним лучом, если вниз — нижним лучом.

Прямые и лучи в пространстве

Луч — это также бесконечно длинная линия, но отличается от прямой тем, что имеет начальную точку. Луч продолжается бесконечно вдоль определенного направления, но начинается с определенной точки.

Прямые и лучи играют важную роль в геометрии и алгебре. Они используются для определения и описания геометрических фигур, а также для решения уравнений и систем уравнений.

Прямые и лучи могут пересекаться, образуя точку пересечения. Они также могут быть параллельными, если они не пересекаются ни в одной точке. В пространстве может быть множество прямых и лучей, которые могут иметь различные направления и положения.

Прямые и лучи могут быть описаны с помощью математических уравнений или геометрических конструкций. Они могут быть использованы для моделирования физических объектов, таких как лучи света или пути движения объектов.

Изучение прямых и лучей позволяет нам лучше понять и описать мир вокруг нас, используя язык математики. Это важные понятия, которые находят применение во многих областях науки и техники.

Положение луча относительно фигур

Положение луча относительно фигур может быть различным:

1. Луч, проходящий внутри фигуры: в этом случае луч целиком находится внутри фигуры и не выходит за ее границы.

2. Луч, пересекающий фигуру: в данном случае луч начинается вне фигуры, пересекает ее границу и продолжается дальше.

3. Луч, не пересекающий фигуру: такой луч не имеет точек пересечения с фигурой и проходит снаружи ее границы.

4. Луч, касательный к фигуре: в этом случае луч касается границы фигуры в одной точке и проходит вне ее.

5. Луч, лежащий внутри фигуры: в данном случае луч полностью лежит внутри фигуры и не имеет точек пересечения с ее границей.

6. Луч, совпадающий с границей фигуры: такой луч совпадает с границей фигуры и имеет бесконечное количество точек пересечения с ней.

Таким образом, положение луча относительно фигур может быть разнообразным и зависит от их геометрических свойств.

Примеры использования лучей в решении задач

Лучи широко применяются в математике для решения различных задач. Ниже приведены несколько примеров использования лучей:

Пример 1: Пусть дано прямоугольное поле, на котором находятся две точки A и B. Необходимо найти длину отрезка AB. Для решения этой задачи можно провести луч из точки A, проходящий через точку B. Точка пересечения луча и прямоугольника будет являться конечной точкой отрезка AB. Используя свойства лучей, можно определить длину этого отрезка.

Пример 2: Пусть дан треугольник ABC, в котором известны длины сторон AB и AC, а также известен угол между этими сторонами. Необходимо найти длину стороны BC. Для решения этой задачи можно провести луч из вершины B, проходящий через вершину C. Точка пересечения луча и стороны AB будет являться конечной точкой стороны BC. Используя свойства лучей, можно определить длину этой стороны треугольника.

Пример 3: Пусть дан отрезок AB на числовой прямой, на котором известны координаты начальной точки A и конечной точки B. Необходимо найти координату точки C, которая находится на этом отрезке так, что AC в 2 раза меньше, чем BC. Для решения этой задачи можно провести луч, начинающийся в точке C и проходящий через точку B. Точка пересечения луча и отрезка AB будет являться искомой точкой C. Используя свойства лучей, можно найти координату этой точки.

Таким образом, лучи являются полезным инструментом для решения различных задач в математике. Они позволяют проводить линии в определенном направлении и находить точки пересечения с другими фигурами или линиями.

Видео по теме:

Что такое луч в математике?

Луч в математике — это часть прямой, которая начинается в одной точке и простирается бесконечно в одном направлении.

Как найти точку пересечения двух лучей?

Для нахождения точки пересечения двух лучей необходимо решить систему уравнений, где уравнения задают эти лучи. Если система имеет решение, то найденная точка будет являться точкой пересечения лучей.

Может ли луч пересекать другую прямую?

Да, луч может пересекать другую прямую. Если луч и прямая пересекаются в одной точке, то эта точка будет являться точкой пересечения.

Может ли луч иметь длину?

Нет, луч не имеет длины, так как он простирается бесконечно в одном направлении. Луч можно представить как бесконечное расширение от начальной точки.

Что такое луч в математике?

Луч — это часть прямой, состоящая из начальной точки и всех точек, лежащих по одну сторону от нее.